初中数学浙教版（2024）九年级下册第三章 投影与三视图3.1 投影习题

这是一份初中数学浙教版（2024）九年级下册第三章 投影与三视图3.1 投影习题，共9页。试卷主要包含了下列投影是平行投影的是等内容，欢迎下载使用。
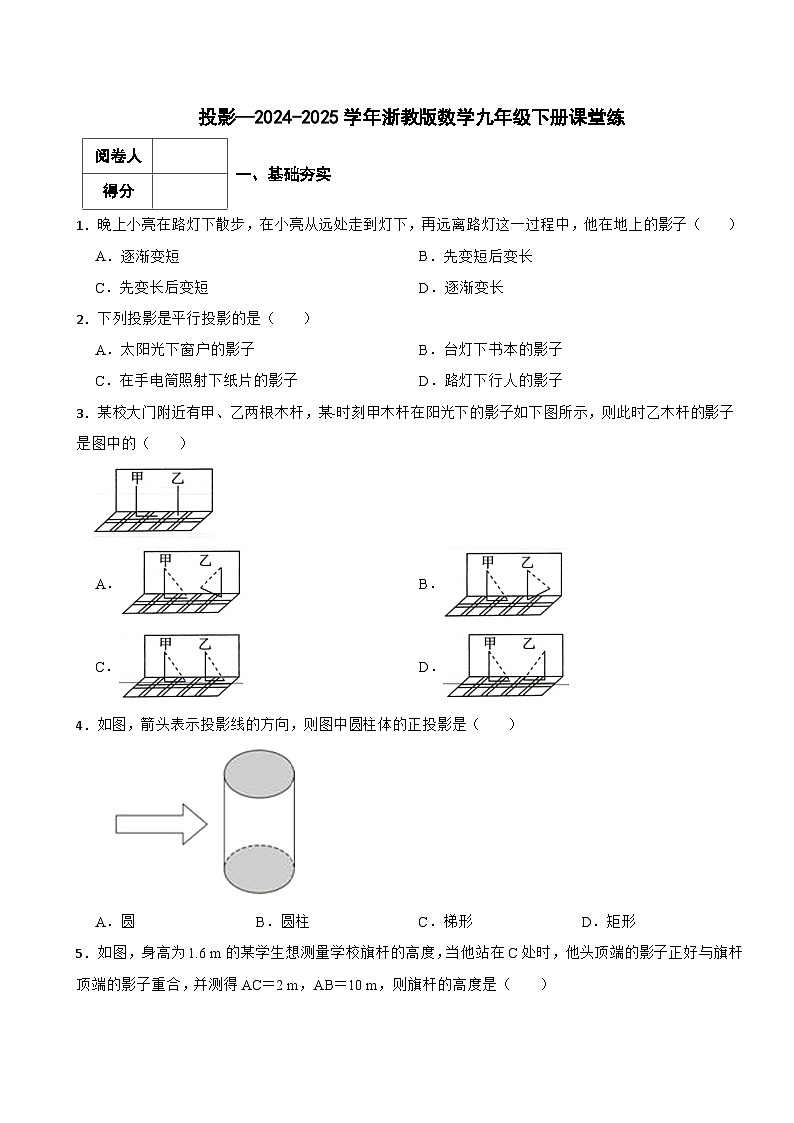
1．晚上小亮在路灯下散步，在小亮从远处走到灯下，再远离路灯这一过程中，他在地上的影子（ ）
A．逐渐变短B．先变短后变长
C．先变长后变短D．逐渐变长
2．下列投影是平行投影的是（ ）
A．太阳光下窗户的影子B．台灯下书本的影子
C．在手电筒照射下纸片的影子D．路灯下行人的影子
3．某校大门附近有甲、乙两根木杆，某-时刻甲木杆在阳光下的影子如下图所示，则此时乙木杆的影子是图中的（ ）
A．B．
C．D．
4．如图，箭头表示投影线的方向，则图中圆柱体的正投影是（ ）
A．圆B．圆柱C．梯形D．矩形
5．如图，身高为1.6 m的某学生想测量学校旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC＝2 m，AB＝10 m，则旗杆的高度是（ ）
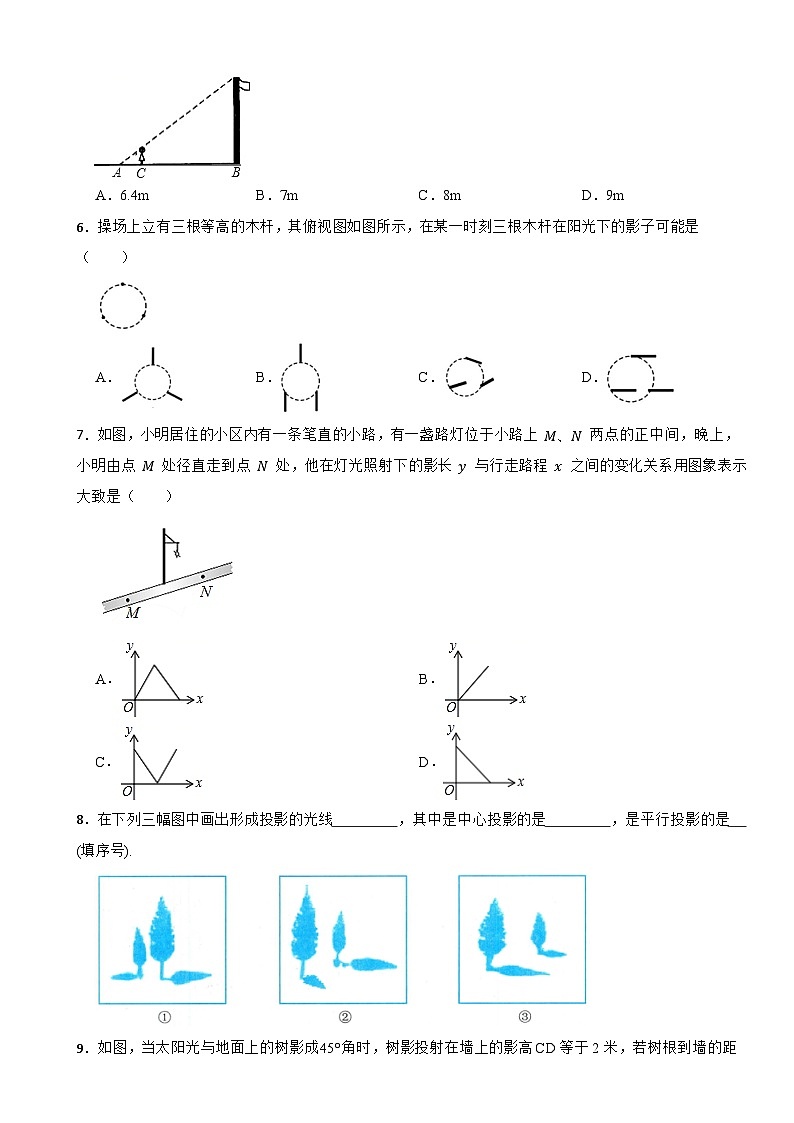
A．6.4mB．7mC．8mD．9m
6．操场上立有三根等高的木杆，其俯视图如图所示，在某一时刻三根木杆在阳光下的影子可能是（ ）
A．B．C．D．
7．如图，小明居住的小区内有一条笔直的小路，有一盏路灯位于小路上 M、N 两点的正中间，晚上，小明由点 M 处径直走到点 N 处，他在灯光照射下的影长 y 与行走路程 x 之间的变化关系用图象表示大致是（ ）
A．B．
C．D．
8．在下列三幅图中画出形成投影的光线 ，其中是中心投影的是 ，是平行投影的是 (填序号).
9．如图，当太阳光与地面上的树影成45°角时，树影投射在墙上的影高CD等于2米，若树根到墙的距离BC等于8米，则树高AB等于 米．
10． 如图，路灯下一墙墩（用线段AB表示）的影子是BC，小明（用线段DE表示）的影子是EF，在M处有一棵大树，它在这个路灯下的影子是MN．
（1）在图中画出路灯的位置并用点P表示；
（2）在图中画出表示大树的线段MQ．
11．如图，小聪和他同学利用影长测量旗杆的高度，当1米长的直立的竹竿的影长为1.5米时，此时测得旗杆落在地上的影长为12米，落在墙上的影长为2米，则旗杆的实际高度为（ ）
A．8米B．10米C．18米D．20米
12．如图，丁轩同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行20 m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是1.5 m，两个路灯的高度都是9 m，则两路灯之间的距离是( )
A．24 mB．25 mC．28 mD．30 m
13．如图，太阳光线与地面成60°的角，照射在地面上的一个皮球上，皮球在地面上的投影的最大长度是103cm，则皮球的直径是 cm．
14． 如图，小树AB在路灯O的照射下形成投影BC．
（1）此光源下形成的投影属于 ．（填“平行投影”或“中心投影”）
（2）已知树高AB为2m，树影BC为3m，树与路灯的水平距离BP为4.5m．求路灯的高度OP．
15．完成下列各题：
（1）三根垂直地面的木杆甲、乙、丙，在路灯下乙．丙的影子如图1所示．试确定路灯灯泡的位置，再作出甲的影子．（不写作法，保留作图痕迹）
（2）如图2，在平行四边形ABCD中，点E，F分别在AB，CD上，AE=CF．求证：DE=BF．
16．小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试．
（1）如图1，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其上方点P处有一灯泡，在灯泡的照射下，正方形框架的横向影子A'B，D'C的长度和为6cm.那么灯泡离地面的高度PM为多少．
（2）不改变图1中灯泡的高度，将两个边长为30cm的正方形框架按图2摆放，请计算此时横向影子A'B，D'C的长度和为多少？
17．【综合与实践】现实生活中，人们可以借助光源来测量物体的高度．已知榕树CD，FG和灯柱AB如图①所示，在灯柱AB上有一盏路灯P，榕树和灯柱的底端在同一水平线上，两棵榕树在路灯下都有影子，只要测量出其中一些数据，则可求出所需要的数据，具体操作步骤如下：
①根据光源确定榕树在地面上的影子；
②测量出相关数据，如高度，影长等；
③利用相似三角形的相关知识，可求出所需要的数据．
根据上述内容，解答下列问题：
（1）已知榕树CD在路灯下的影子为DE，请画出榕树FG在路灯下的影子GH；
（2）如图①，若榕树CD的高度为3.6米，其离路灯的距离BD为6米，两棵榕树的影长DE，GH均为4米，两棵树之间的距离DG为6米，求榕树FG的高度；
（3）无论太阳光还是点光源，其本质与视线问题相同．日常生活中我们也可以直接利用视线解决问题．如图②，建筑物CD高为50米，建筑物MF上有一个广告牌EM，合计总高度EF为70米，两座建筑物之间的直线距离FD为30米．一个观测者（身高不计）先站在A处观测，发现能看见广告牌EM的底端M处，观测者沿着直线AF向前走了5米到B处观测，发现刚好看到广告牌EM的顶端E处．则广告牌EM的高度为 米．
答案解析部分
1．【答案】B
2．【答案】A
3．【答案】C
4．【答案】D
5．【答案】C
6．【答案】D
7．【答案】C
8．【答案】；①②；③
9．【答案】10
10．【答案】（1）解：见解析：如图，点P即为所求，
（2）解：见解析：如图，线段MQ即为所求．
11．【答案】B
12．【答案】D
13．【答案】15
14．【答案】（1）中心投影
（2）解：
由题意得：AB⊥CP，OP⊥CP，
∴∠OPC∠ABC=90°
∵∠OCP=∠ACB，∴△CAB∽△COP，
∴ABOP=BCPC，即2OP=33+4.5，
解得：OP=5
答：路灯的高度OP为5m．
15．【答案】（1）解：如图所示：AB即为甲的影子；
（2）证明：∵在平行四边形ABCD中，
∴CD=AB，CD∥AB，
∵AE=CF，
∴DF=BE，
又∵CD∥AB，
∴四边形DEBF是平行四边形，
∴DE=BF．
16．【答案】（1）解：∵AD//A'D'，
∴∠PAD=∠PA'D'，∠PDA=∠PD'A'．
∴△PAD∽△PA'D'．
根据相似三角形对应高的比等于相似比的性质，可得ADA'D'=PNPM，
∴3036=PM−30PM，
解得PM=180．
∴灯泡离地面的高度PM为180cm；
（2）解：设横向影子A'B，D'C的长度和为ycm，
同理可得6060+y=150180，
解得y=12．
即横向影子A'B，D'C的长度和为12cm．
17．【答案】（1）解：图①中GH即为所求；
（2）解：∵CD∥PB，
∴△ECD∽△EPB，
∴CDPB=EDEB，即3.6PB=44+6，
解得：PB=9，
∵FG∥PB，
∴△HFG∽△HPB，
∴FGPB=HGHB，即FG9=44+6+6，
解得：FG=94，
答：榕树FG的高度为94米；
（3）54阅卷人
一、基础夯实
得分
阅卷人
二、能力提升
得分
阅卷人
三、拓展创新
得分