北京课改版数学九下 25.1《求概率的方法》课件

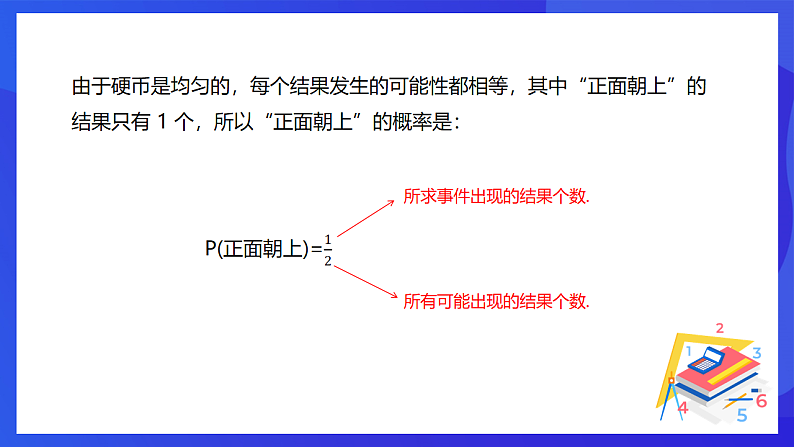
25.1《求概率的方法》在日常生活中，我们会遇到很多概率问题北京气象台天气预报:“明天白天，阴转小雨，降水概率 60%…瓶盖掉在地上，盖面朝上的概率有多大?在商场购物得到一张抽奖券，中奖的概率有多大?水平相当的甲、乙两队进行排球比赛，规定五局三胜，甲队以3:0战胜乙队的概率有多大?......这一章，我们要学习求概率的方法，并学会解决生活中一些简单事件的概率问题。章节导入目标1目标21.掌握在具体情境中概率的意义，会解释具体事件概率的含义;目标32.了解用列表法计算随机事件发生的概率。3.掌握使用频率估算概率的方法。学习目标仔细阅读教材P62---P69。用3分钟的时间看谁又快又好地解决以下问题：1.什么是列举法？2.用频率估计概率是怎么操作的？自学指导前面我们已经学习过，事件可以分为必然事件、不可能事件和随机事件.还知道，事件发生的可能性可以用数值表示，如P(必然事件)=1，P(不可能事件)=0.表示一个事件发生的可能性大小的数值，称为这个事件的概率，记作P(事件).例如，降水概率是 60%，是指降水的可能性是 60%.现在，我们来学习求概率的方法.回顾列举法 我们曾做过抛掷一枚硬币的实验，硬币落地后，所有可能出现的结果有 2 个，如图所示，  所求事件出现的结果个数.所有可能出现的结果个数.由于硬币是均匀的，每个结果发生的可能性都相等，其中“正面朝上”的 结果只有 1 个，所以“正面朝上”的概率是：每位同学同时抛掷两枚硬币，观察两枚硬币落地后的情况： ( 1 ) 两枚硬币落地后，可能出现的结果有几种 ? ( 2 ) 两枚硬币落地后，正面都朝上的概率有多大 ?假设抛掷的分别是 A，B 两枚硬币，落地后硬币 A 所有可能出现的结果如下表的左列所示，硬币 B 所有可能出现的结果如下表的上行所示，两枚硬币所有可能同时出现的结果如下表所示：列表法上面是用列表的方法列举所有可能出现的结果，有下面 4 个： ( 正，正 ) ；( 正，反 ) ；( 反，正 ) ；( 反，反 ) . 由于两枚硬币都是均匀的，每个结果发生的可能性都相等，其中出现“两 枚正面都朝上”的结果有 1 个 . 所以 这样计算的根据是什么？直接列举法我们也可以先列举硬币 A 所有可能出现的结果，在它的每个结果后面再分别列举硬币B所有可能出现的结果，由此得到 A，B 两枚硬币所有可能同时出现的结果，如图所示：树状法上面是用画树状图的方法列举所有可能出现的结果 . 用列举法求概率的一般步骤是： ( 1 ) 列举 ( 列表、画树状图 ) 事件所有可能出现的结果，并判断每个结果发生的可能性是否都相等； ( 2 ) 如果都相等，再确定所有可能出现的结果个数 n 和其中出现所求事件A 的结果个数 m ； ( 3 ) 用公式计算所求事件 A 发生的概率 . 即 列举法求概率的一般步骤知识要点例1 在五张大小相同的卡片上，分别写有数字 0，1，1，2，2，把写有 1，2 的两张卡片放在左边，把另外写有 0，1，2 的三张卡片放在右边，并且写有数字的面都朝下 . ( 1 ) 分别从左、右两边随机各取出一张卡片，求这两张卡片上的数字之和为奇数的概率； ( 2 ) 将右边的三张卡片随机排成一行，求翻开后组成一个三位数的概率 .典型例题分析：只需列举所有可能发生的结果，并确定每个结果发生的可能性都相等 . ( 1 ) 将取出的左、右两边两张卡片上的数字求和，所有可能出现的结果如下表所示：( 2 ) 右边三张卡片随机排成一行，翻开后，所有可能出现的结果如图右列所示： 为什么每个结果发生的可能性都相等？ 要确定每个结果发生的可能性相等！例2 口袋里有四枚除颜色外都相同的棋子，其中有三枚是红色的，一枚是黑色的 . 从中随机同时摸出两枚，求摸出的两枚棋子颜色不同的概率 .分析：只需列举同时摸出两枚棋子的所有可能结果 . 为防止遗漏或重复，给三枚红色棋子编号为红1、红 2、红 3 . 结果如图所示： 例3 口袋里有三枚除颜色外都相同的棋子，其中有两枚是红色的，一枚是黑色的 . 从中随机摸出一枚记下颜色，放回口袋搅匀，再从中随机摸出一枚记下颜色 . 求两次摸出棋子颜色不同的概率 . 分析：这是有放回的两次摸出棋子的问题，也就是每次都是从三枚棋子中 随机摸出一枚 . 列举两次摸出棋子的所有可能结果，如下表所示：这里的( 红2，红1 )与( 红1，红2 ) 为什么不一样？ 抛掷一枚硬币时，我们可以通过列举法求得硬币落地后“正面朝上”的概率 . 如果把硬币换成瓶盖 ，如图，怎样求瓶盖掉在地上后，盖面朝上的概率呢？探索抛掷一枚瓶盖，落地后会出现哪些结果，每个结果发生的可能性相等吗？为什么？还能用前面的公式计算概率吗？如果不能，怎样求盖面朝上的概率？全班同学分成两大组 . 第一大组的同学都抛掷同一型号的一枚瓶盖， 第二大组的同学都抛掷同一面额的硬币，以 2 人为一小组各抛掷 50 次，记下落地后盖 ( 正 ) 面朝上的次数，统计本小组 50 次实验中盖 ( 正 ) 面朝上的次数和频率，各大组依次累计各小组的实验结果，填在下表中（频率精确到 0.0001）在图中画出上表中盖 ( 正 ) 面朝上的频率折线图 .从实验中知道，瓶盖或硬币落地后，所有可能出现的结果有 2 个：“盖 ( 正 ) 面朝上”和“盖 ( 正 ) 面朝下”. 由于瓶盖不均匀，每个结果发生的可能性不相等，因此，不能用前面的公式计算盖面朝上的概率 . 观察两个大组完成的频率折线图，我们发现，重复实验的次数不同，盖 ( 正 ) 面朝上的频率也可能不同，但总是在某个常数附近波动，我们就把这个常数作 为盖 ( 正 ) 面朝上的概率 . 一般地，在做大量重复实验时，如果一个事件发生的频率总是在某个常数附近波动，就把这个常数作为这个事件发生的概率 . AC基础检测某学校将在10月举行运动会，要在九（2）班学生中选两名学生作志愿者，该班现有3名男生和2名女生报名，则恰好挑选的是一男一女的概率是　 ． 一展身手2024年10月19日，学校举办建校160周年校庆的校友返校活动．为了保证返校活动顺利进行，学校在非毕业年级校区的各个班级中招募志愿者，小明和小然积极报名参加．根据学校安排，志愿者将被随机分到A组（精美礼物发放），B组（行进路线指引），C组（学校校史介绍）中的其中一组进行志愿工作．（1）小明被分配到A组是 　 　事件，小亮被分配到B组是 　 　事件（填“必然”，“随机”或“不可能”）；（2）请用列表或画树状图的方法，求出小明和小然被分配到同一组的概率．随机不可能挑战自我解：（1）由题意得，小明被分配到A组是随机事件，小亮被分配到B组是不可能事件，故答案为：随机；不可能；（2）画树状图如下： 求概率的方法1.直接列举法2.列表法3.树状法4.用频率估算概率课堂小结