2025年中考复习数学第07讲 一元二次方程及其应用（课件）

这是一份2025年中考复习数学第07讲 一元二次方程及其应用（课件），共60页。PPT课件主要包含了一元二次方程及其解法，变化率问题，利润问题，循环问题，面积问题，其它问题，等号右边是0，易错热考，一元二次方程，两个一元一次方程等内容，欢迎下载使用。
一元二次方程根的判别式
一元二次方程根与系数的关系
理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程
会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等
了解一元二次方程的根与系数的关系
【考情分析1】本专题包括利用根的判别式确定一元二次方程解的情况、已知方程解的情况确定方程中未知字母的值及利用根与系数关系求解某些特定形式的代数式的值,试题形式多样，难度一般，常与完全平方公式的各种变形结合考查.
一元二次方程的实际应用
能根据现实情境理解方程的意义；能针对具体问题列出方程；能根据具体问题的实际意义，检验方程解的合理性.
【考情分析2】一元二次方程的应用的考查多以解答题形式出现，难度一般，主要涉及的问题有变化率问题、利润问题、几何图形问题等. 解决实际问题时，要检验所求解是否满足实际意义，注意取舍.
【命题预测 】本考点内容以考查一元二次方程的相关概念、解一元二次方程、根的判别式、韦达定理（根与系数的关系）、一元二次方程的应用题为主，既有单独考查，也有和二次函数结合考察最值问题，年年考查，分值为15分左右.预计2025年各地中考还将继续考查上述的几个题型，复习过程中要多注意各基础考点的巩固，特别是解法中公式法的公式，不要和后续二次函数顶点坐标的纵坐标公式记混了．
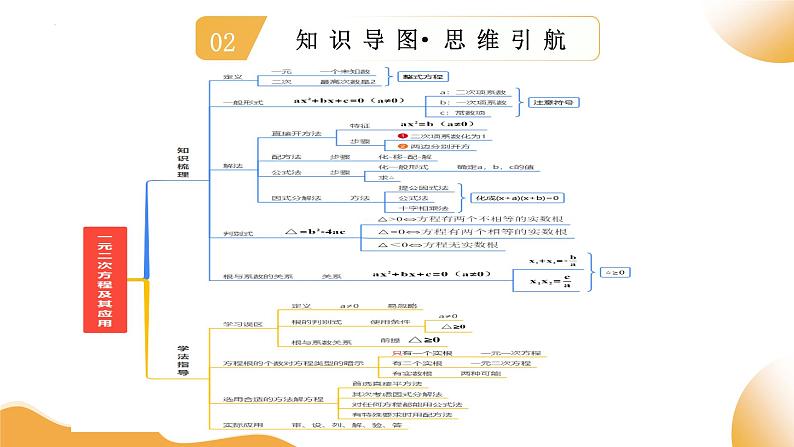
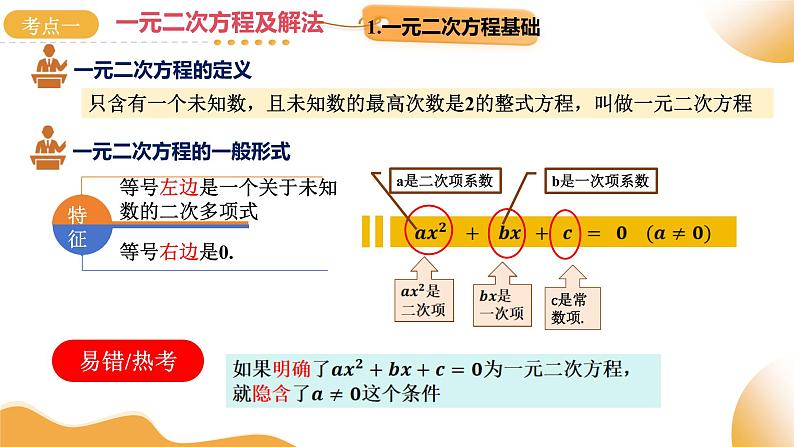
只含有一个未知数，且未知数的最高次数是2的整式方程，叫做一元二次方程
等号左边是一个关于未知数的二次多项式
能使一元二次方程左、右两边相等的未知数的值叫做一元二次方程的解（根）.
将此数代入这个一元二次方程的左、右两边，看左右两边的值是否相等，若相等，则是方程的根；若不相等，则不是方程的根.
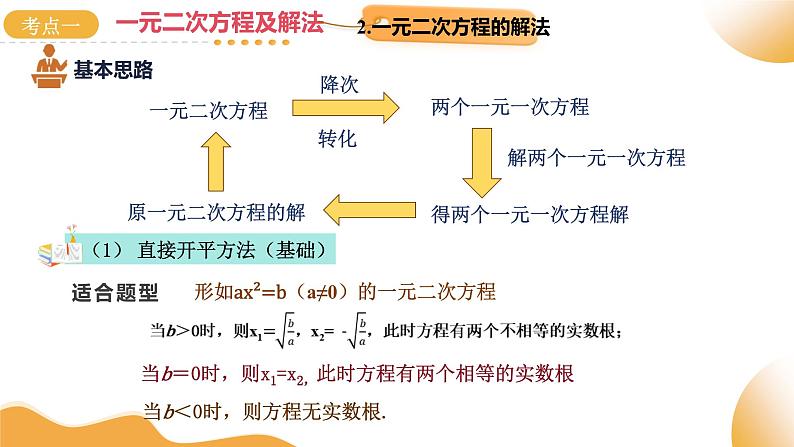
形如ax²=b（a≠0）的一元二次方程
当b＝0时，则x1=x2，此时方程有两个相等的实数根
当b＜0时，则方程无实数根.
将方程化为（ax+b）²=m(a≠0)形式
当m≥0时，直接用直接开平方法求解.
用配方法解一元二次方程的一般步骤：
将常数项移到等号右边,含未知数的项移到等号左边；
如果二次项系数不是1，将方程两边同时除以二次项系数；
方程两边都加上一次项系数一般的平方，把方程化为（x+p）²=q
求解：若q≥0时，直接用直接开平方法求解
用公式法解一元二次方程的一般步骤：
【补充说明】求根公式的使用条件
如果两个一次因式的积为0，那么这两个因式中至少一个为0，即
若ab=0，则a=0或b=0.
用因式分解法解一元二次方程的一般步骤：
利用因式分解法解方程时，含有未知数的式子可能为零，所以在解方程时，不能在两边同时除以含有未知数的式子，以免丢根，需通过移项,将方程右边化为0.
通常用希腊字母Δ表示：
方程有两个不相等的实根
【补充说明】一元二次方程有解分两种情况：1）有两个相等的实数根； 2）有两个不相等的实数根．
2）当Δ= b²-4ac=0时，方程有两个相等的实数根，不能说方程只有一个实数根
1）使用一元二次方程根的判别式时，应先将方程整理成一般形式，再确定a，b，c的方程；
∴方程有两个不相等的实数根，综上，方程有1个或2个解，
4）运用根与系数的关系和运用根的判别式一样,都必须先把方程化为一般形式，以便正确确定a、b、c的值.
1）一元二次方程根与系数关系的使用条件：
3）以两个数x1,x2为根的一元二次方程（二次项系数为1）是
x1+x2＝-p， x1•x2＝q.
a (1 ± x ) n = b
增长（或降低）的次数
增长（或降低）的基础数
增长（或降低）的变化率
增长（或降低）后的数量
(a−2x)(b−2x)（x为空白部分的宽）
(a−x)(b−x)（x为阴影部分的宽）
a (1±x ) n = b
3．（2021·山西·中考真题）2021年7日1日建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数（请用方程知识解答）．
日历的特征：左右相差1，上下相差7
已知a，b，c分别为二次项系数，一次项系数，常数项.1）当a=1，b为偶数，c≠0时，首选配方法；2）当b=0时，首选直接开平方法；3）当c=0时，可选因式分解法或配方法；4）当a=1，b≠0，c≠0时，可选配方法或因式分解法；5）当a≠1，b≠0，c≠0时，可选公式法或因式分解法.
灵活选取适当的方法解方程
b²-4ac=25-16=9
熟练掌握一元二次方程各种解法的主要步骤
你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．
方程两边不能同时除以含未知数的代数式
提公因式后去括号符号不对
(1)判断：两位同学的解题过程是否正确，若正确，请在框内打“√”；若错误，请在框内打“×”．(2)请选择合适的方法求解此方程．
（1）两位同学的解题过程都不正确．
因式分解法解方程时要化简方程为A×B=0的形式
【利用配方法求代数式的最值】
运用配方法将代数式化为非负数与常数代数和形式
模仿求解过程，利用配方法进行求解
以开放性试题的形式考查直接解一元二次方程，解题时可以根据题目选择不同的方法解决问题有利于培优策略性思维。
解：任选两个方程解答如下
1）有根Δ≥ 0; 2）有两个不等根Δ＞0;3）有两个相等根Δ= 0; 4）无实数根Δ＜0.
∵方程有两个不相等的实数根
利用跟的判别式确定p的取值范围
直接代入方程判断方程的解的情况，再确定p的取值
【例1】 （2024·山东淄博·中考真题）“我运动，我健康，我快乐！”随着人们对身心健康的关注度越来越高．某市参加健身运动的人数逐年增多，从2021年的32万人增加到2023年的50万人．(1)求该市参加健身运动人数的年均增长率；
2．（2023·湖南郴州·中考真题）随旅游旺季的到来，某景区游客人数逐月增加，2月份游客人数为1.6万人，4月份游客人数为2.5万人．(1)求这两个月中该景区游客人数的月平均增长率；
(2)预计5月份该景区游客人数会继续增长，但增长率不会超过前两个月的月平均增长率．已知该景区5月1日至5月21日已接待游客2.125万人，则5月份后10天日均接待游客人数最多是多少万人？
AB × BC = 640
AB × BC = 650
(1)八进制数3746换算成十进制数是_______；