北师大版（2024）七年级上册（2024）1 代数式优秀备课课件ppt

这是一份北师大版（2024）七年级上册（2024）1 代数式优秀备课课件ppt，共49页。PPT课件主要包含了学习目标，情景导入，新知探究，概念归纳，尝试思考，课堂练习，分层练习-基础，分层练习-巩固，分层练习-拓展，课堂小结等内容，欢迎下载使用。
1. 经历观察、分析、交流，概括出单项式、多项式、整式的概念，发展有条理的思考能力及语言表达能力。2. 通过交流研讨活动，培养学生主动与他人合作的意识。重点：掌握整式及多项式的有关概念。难点：准确判断多项式的次数。
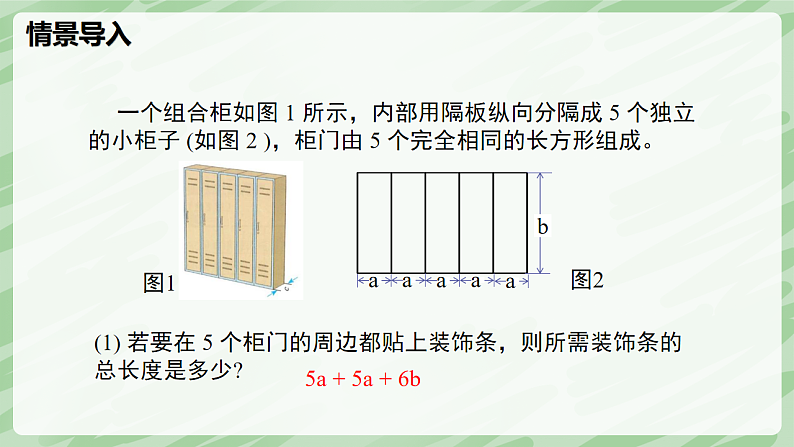
一个组合柜如图 1 所示，内部用隔板纵向分隔成 5 个独立的小柜子 (如图 2 )，柜门由 5 个完全相同的长方形组成。
(1) 若要在 5 个柜门的周边都贴上装饰条，则所需装饰条的总长度是多少?
5a + 5a + 6b
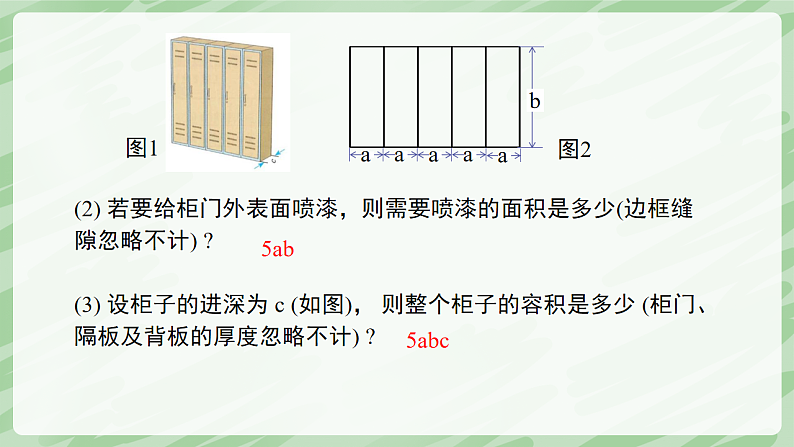
(2) 若要给柜门外表面喷漆，则需要喷漆的面积是多少(边框缝隙忽略不计) ?(3) 设柜子的进深为 c (如图)， 则整个柜子的容积是多少 (柜门、隔板及背板的厚度忽略不计) ?
像5ab，5abc，3v，6p等，它们都是数与字母的乘积，这样的代数式叫作单项式. 单独一个数或一个字母也是单项式.
单项式中的数字因数叫作这个单项式的系数，如5ab的系数是5，3v的系数是3。所有字母的指数和叫作这个单项式的次数，如5ab是2次的，3v是1次的。
在多项式中，每个单项式叫作多项式的项，如多项式10x+5y是10x与5y两项的和。一个多项式中，次数最高的项的次数，叫作这个多项式的次数。如10x+5y是1次的，a²b+2a是3次的。
像5ab，5abc，3v，6p等，它们都是数与字母的乘积，这样的代数式叫作单项式.
请列出下列问题中的代数式，并指出其中：① 哪些是单项式? 单项式的系数和次数分别是多少?② 哪些是多项式? 多项式的次数是多少?
(1) 如图，一个十字形花坛铺满了草皮，这个花坛草地面积是多少?
多项式，次数是 2 次。
(3) 如图，一个长方体的箱子紧靠墙角，它的长、宽、高分别是 a，b，c。这个箱子露在外面的表面积是多少？
ab + ac + bc
(4) 某件商品的成本价为 a 元，按成本价提高 15% 标价，后又以八折 (即按标价的 80% ) 销售，这件商品的售价为多少元？
0.8(1 + 15%)a 元
多项式，次数是 1 次。
1.将下列代数式中的单项式和多项式分别填入所属的圈中，并指出其中：各单项式的系数分别是多少？多项式中哪个次数最高？次数是多少？
1.用代数式表示：（1）f 的11倍再加上2可以表示为_______;（2）一个数a的 与这个数的和可以表示为 ；
（5）某班共有x个学生，其中女生人数占45%，那么男生人数是 。
（3）一个教室有2扇门和4扇窗户，n个这样的教室有_____扇门和 _____扇窗户;（4）产量由mkg增长15％后，达到____________ kg．
2.人体血液的质量占人体体重的7%~8%。(1)如果某人体重是akg，那么他的血液质量大约在什么范围内?(2)小亮体重是35kg，他的血液质量大约在什么范围内?(3)估计你自己的血液质量。
解：(1)这个人的血液质量大约在6%akg到7.5%a kg之间. (2)亮亮的血液质量大约在2.1 kg 到2.625 kg 之间. (3)略.
3. 物体由静止自由下落的高度h(单位: m)和下落时间t(单位: s)之间 的关系，在地球上大约是h=4.9t2，在月球上大约是h=0.8t。
(2)物体在地球，上下落得较快还是在月球上下落得较快?(3)当h=20m时，比较物体在地球.上和在月球上自由下落所需的时间。
解：(2)地球. (3)当h=20 m时， 物体在地球上自由下落所需的时间约为2s, 物体在月球上自由下落所需的时间约为5s.
4. 声音在干燥空气中传播的速度随着温度的变化而变化，当温度 为 t ℃ 时，声音的传播速度(单位: m/s)大约是331+0.6t，求温度 分别为 2 ℃和 30 ℃时声音的传播速度。
解：当t=2 9℃时，331 +0.6t= 331 +0.6×2= 332.2( m/s).当t=30 ℃时，331 +0.6t= 331+30×2=391( m/s).所以温度分别为2 C和30 C时声音的传播速度分别是332.2 m/s,391 m/s.
5.观察右图，回答下列问题：（1）标出未注明的边的长度；（2）阴影部分的周长是_________;（3）阴影部分的面积是___________;（4）当x=5.5，y=4时，阴影部分的周长是______,面积是______.
（4xy-0.5xy）
6. 某物体由静止竖直向上运动，物体的高度h(单位: m)与运动时间t(单位:s)之间的关系可以用公式h=-5t2+ 150t+ 10表示，求运动时间分别为10s，15s, 20s时该物体的高度。
答：运动时间分别为 10 s，15 s，20 s 时该物体的高度分别 1010m，1135m，1010m.
解：图中运算过程是（x2+y3）÷2.
7. 下图是一个“数值转换机”的示意图，写出运算过程并填写下表.
解：单项式：7h，次数为1； 多项式：xy³+1，2ab+6， x－by³， 次数分别是4，2，4.
8.下列代数式中哪些是单项式，哪些是多项式？它们的次数分别是多少？ 7h， xy3+1， 2ab+6， x−by3．
解：（1）3项，第一项系数为 ，次数为1；第二项系数为－1， 次数为3；第三项系数为2π，次数为0. （2）3项，第一项系数为1，次数为3；第二项系数为－2， 次数为4；第三项系数为3，次数为2.
9.下列多项式分别有几项？每项的系数和次数分别是多少？ （1）− x−x2y+2π； （2）x3-2x2y2+3y2.
10. (1)小明用棋子按如图所示的规律摆出图形，并写出1 +3n的结果，请解释他的想法。
解：(1)由图形摆放规律知第1个图形有棋子4枚,即4=1+3,且每增加1个图形,棋子枚数增加3,故第n个图形棋子的枚数为1+3n。
(2)与本节“用小棒拼摆正方形”活动中得到的结果相比较，你在(1)中有什么发现?(3)用99枚棋子能恰好摆出符合(1)中规律的图形吗?用100枚呢?
(2)提示:可借助字母表示“四点”图形个数与棋子枚数之间的关系。(3)用99枚棋子不能拼摆出符合(1)中规律的图形, 100枚可以恰好拼摆出。
11. 下列代数式可以表示什么？（1）2x （2） （3）8a3
解：(1) 1斤梨x元，买2斤梨所花的费用
(2) a，b的和的一半
(3) 棱长为a的正方体体积的8倍
解：（1）随着n的值逐渐变大，两个代数式的值都逐渐减小.
12. 填写下表，并观察-8n+5和-n2这两个代数式的值的变化情况。
（1）随着n值的逐渐变大，-8n+5和-n2这两个代数式的值如何变化？
（2）－n²的值先小于－100.
（2）估计一下，哪个代数式的值先小于－100？
13.用火柴棒按下面的方式搭图形：
(1) 小明用长度相同的小棒按如图所示的规律拼摆图形，第n个图形需要多少根小棒?
解：第n个图形需要[7+5（n－1）]根，即（5n+2）根火柴棒.
(2) 小颖给出一种新的拼摆方式，按照小颖的方式拼摆,第n个图形所需小棒的根数为 3+2(n-1 )。请你画图表示小颖的拼摆方式。
(3)请你设计出其他有规律的拼摆方式，根据你的拼摆规律提出问题并加以解决。
(3)拼摆方式如图(2)所示。问题：摆放第8个图形需要多少根小棒?解答：8×8+3 = 67(答案不唯一)。
解：（1）设蟋蟀1min叫的次数为x，则温度可以表示为（ ）℃;
14.在某地，人们发现在一定气温下某种蟋蟀叫的次数与气温之间有如下的近似关系:用蟋蟀1 min叫的次数加30，再把结果除以7,就近似地得到该地当时的气温(单位: ℃)。（1）用代数式表示当时的温度；
（2）当x=80时，温度约为16℃；当x=100时，温度约为19℃;当x为120时，温度约为21℃.
（2）当蟋蟀1min叫的次数分别是80,100和120时，该地当时的温度是多少？
解：（1）小刚成年后的身高=(a+b)÷2×1.08 =(1.72+1.65)÷2×1.08≈1.82（m）. （2）把自己父母的身高代入公式，预测自己的身高.
15.遗传是影响一个人身高的因素之一.国外有学者总结出用父母身高预测子女身高的经验公式：儿子成年后的身高= ×1.08，女儿成年后的身高= ，其中a为父亲身高，b为母亲身高，单位：m.（1）七年级男生小刚的爸爸身高为1.72m，妈妈身高为1.65m，根据这个公式预测小刚成年后的身高；（2）根据这个公式，预测一下自己成年后的身高.
16. 骑山地自行车过程中，如果车座高度不合适，会使骑行者踩踏费力，甚至造成膝盖磨损。如何确定合适的车座高度呢?有一种雷蒙德( Lemnd)测量方法:双腿站立，两脚(不穿鞋)间距约15cm,测量裆部离地面的高度h(单位:cm),得出的数据乘0.883就是相应的车座顶部到中轴的距离l(如图，单位: cm),此时的车座高度是骑行最合适的高度。根据雷蒙德测量方法解决下列问题:
(1)用代数式表示 l 与 h 之间的关系。
解：(1) 根据题意和雷蒙德测量方法可得: l = 0.883h;
(2) 当h=84cm时, l为多少厘米?
(2)当h = 84cm时，l= 0.883×84 = 74.172 (cm);(3)自测h = 90cm,调整自己山地自行车的车座高度 l = 0.883×90= 79.47 (cm), 经过测试，雷蒙德测量方法适合自己.
(3) 请测量自身的相关数据，计算并调整自己山地自行车的车座高度,检 验雷蒙德测量方法是否适合自己。
17.如图(1)(2)，某餐桌桌面可由圆形折叠成正方形（图中阴影表示可折叠部分）.已知折叠前圆形桌面的直径为am，折叠成正方形后其边长为bm，如果一块正方形桌布的边长为am，并按图(3)所示把它铺在折叠前的圆形桌面上，那么桌布垂下部分的面积是多少？如果按图(4)所示把这块桌布铺在折叠后的正方形桌面上呢？
解：铺在折叠前的圆形桌面上，桌布垂下部分的面积是（a²－ πa²）m²； 铺在折叠后的正方形桌面上，桌布垂下部分的面积是（a²－b²）m².
解：当a=－1，－0.5，1.5，2时，a²－a是正数； 当a=0.5时，a²－a是负数. 当|a|>2时，a²－a是正数.
*18.当a=－1，－0.5，0，0.5，1，1.5，2时，a²－a是正数还是负数？当|a|＞2时，a²－a是正数还是负数？
19.请你设计一个方案，估计一卷空心卷筒纸（如图）展开的总长度。
知识点1　单项式1. (1)表示数与字母的 的代数式叫作单项式，单独 一个 或一个 也是单项式.(2)单项式中的 叫作这个单项式的系数.一个 单项式中，所有字母的指数 ⁠叫作这个单项式的次数.
3. [2024海南中学月考]下列整式中，是二次单项式的是(　B　)
4. 【教材 P 105复习题 T 3变式2023江西改编】单项式－5 ab 的系数为 ，次数为 ⁠.
知识点2　多项式5. 几个 的和叫作多项式.
7. 【易错题】下列说法中，错误的是(　D　)
8. 【新视角·结论开放题】任意写出一个含有字母 m ， n 的 三次四项式，其中最高次项的系数为6，常数项为－8的式 子： ⁠.
6 m3－2 mn ＋ n2－8(答案不唯一)　
9. 已知多项式－25 x2 ym＋1＋ xy2－4 x3－8是五次多项式，单 项式3 x2 ny6－ m 与该多项式的次数相同，则 n ＝ ⁠.
知识点3　整式10. 和 统称整式.如果一个式子既不是多项式也不是单项式，那么它一定不是整式.
11. 下列说法错误的是(　C　)
13. [2024北京丰台区期末]如图是一名同学数学笔记中可见 的一部分.下面四个整式是对这个不完整的整式补充的内 容，则括号里不．能．填(　B　)
(　)＋ xy －5是一个三次三项式
14. 【新视角·新定义题】如果一个多项式的各项的次数都相 同，那么这个多项式叫作齐次多项式.如 x3＋3 xy2＋4 xyz ＋2 y3是3次齐次多项式，若 ax＋3 b2－6 ab3 c2是齐次多项 式，则 x 的值为(　C　)
15. 如果 y｜ m｜－3－( m －5) y ＋16是关于 y 的二次三项式，则 m 的值是 ⁠.
16. 按一定规律排列的单项式：5 a ，8 a2，11 a3，14 a4，…. 则按此规律排列的第 n 个单项式为 .(用含 n 的代数式表示)
(3 n ＋2) an 　
17. 关于 x 的多项式 x4＋( a －1) x3＋5 x2－( b ＋3) x －1中不含 x3项和 x 项，求－ a2 024＋ b3－2 ab 的值.
解：因为关于 x 的多项式 x4＋( a －1) x3＋5 x2－( b ＋3) x －1中不含 x3项和 x 项，所以 a －1＝0，－( b ＋3)＝0.所以 a ＝1， b ＝－3.所以－ a2 024＋ b3－2 ab ＝－12 024＋(－3)3－2×1×(－3)＝ －1－27＋6＝－22.
18. [2024烟台福山区期末]如图，在一个底为 a cm，高为 h cm的三角形铁皮上剪去一个半径为 r cm的半圆.(1)用含 a ， h ， r 的代数式表示剩下铁皮(阴影部分)的面积，并判断这个代数式是单项式还是多项式；
(2)求当 a ＝20， h ＝15， r ＝4时，剩下的铁皮面积.
19. 【新考法·探究归纳法】【探究】(1)当 a ＝5， b ＝3时，分别求多项式① a2－2 ab ＋ b2；②( a － b )2的值.
解：(1)当 a ＝5， b ＝3时，① a2－2 ab ＋ b2＝52－2×5×3＋32＝4，②( a － b )2＝(5－3)2＝4.
【归纳】(3)观察(1)、(2)题中多项式的值，猜想 a2－2 ab ＋ b2与( a － b )2有何关系？
解：(3)由(1)(2)可得 a2－2 ab ＋ b2＝( a － b )2.
【应用】(4)利用你发现的规律，求174.62－2×174.6×74.6＋74.62的值.
解：(4)174.62－2×174.6×74.6＋74.62 ＝(174.6－74.6)2＝10 000.
由数与字母的乘积组成的代数式
多项式中次数最高的项的次数
几个单项式的和叫作多项式