北师大版（2024）七年级下册（2024）3 用关系式表示变量之间的关系备课课件ppt

这是一份北师大版（2024）七年级下册（2024）3 用关系式表示变量之间的关系备课课件ppt，共37页。PPT课件主要包含了想一想，y3x，能确定，和同伴交流一下吧，因变量，含自变量代数式，关系式的基本特征，观察·思考，尝试·交流，基础题等内容，欢迎下载使用。
1.能根据具体情景，用关系式表示变量间的关系.2.并会根据关系式求值，初步体会自变量和因变量的数值对应关系.
数青蛙：一只青蛙一张嘴，两只眼睛四条腿；两只青蛙两张嘴，四只眼睛八条腿；三只青蛙三张嘴，六只眼睛十二条腿……
青蛙的眼睛数和只数有关系吗？能用数学式表达吗？
有，假设青蛙有x只，则青蛙的眼睛数有y只，则数学表达式为y=2x.
y=2x就是用数学表达式表示的变量之间的关系，也是我们本节课要学习的主要内容.
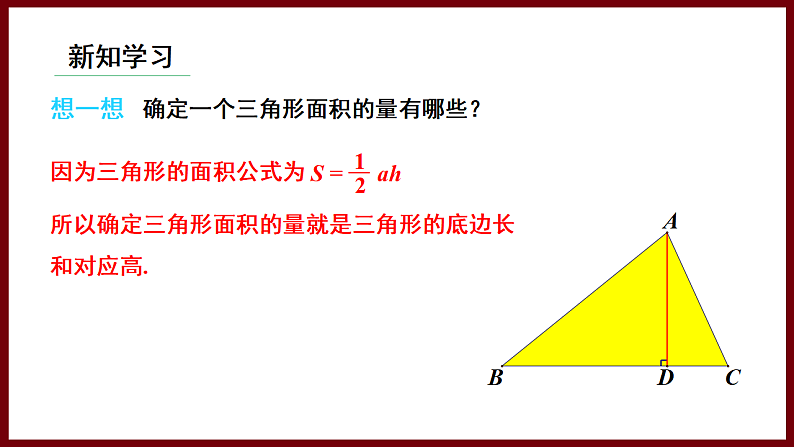
确定一个三角形面积的量有哪些？
所以确定三角形面积的量就是三角形的底边长和对应高.
因为三角形的面积公式为
如图，△ABC底边BC上的高是6 cm. 当三角形的顶点C沿底边所在的直线向点B运动时，三角形的面积发生了变化.
(1)在这个变化过程中，自变量、因变量各是什么？当底边长减小时，三角形的面积是如何变化的？
三角形的底边长度是自变量，三角形的面积是因变量.当底边长减小时，三角形的面积也随之减小.
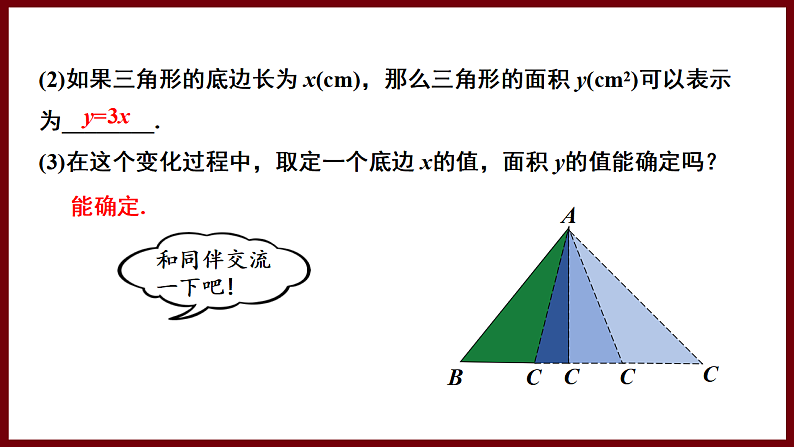
(2)如果三角形的底边长为 x(cm)，那么三角形的面积 y(cm2)可以表示为________.
(3)在这个变化过程中，取定一个底边 x的值，面积 y的值能确定吗？
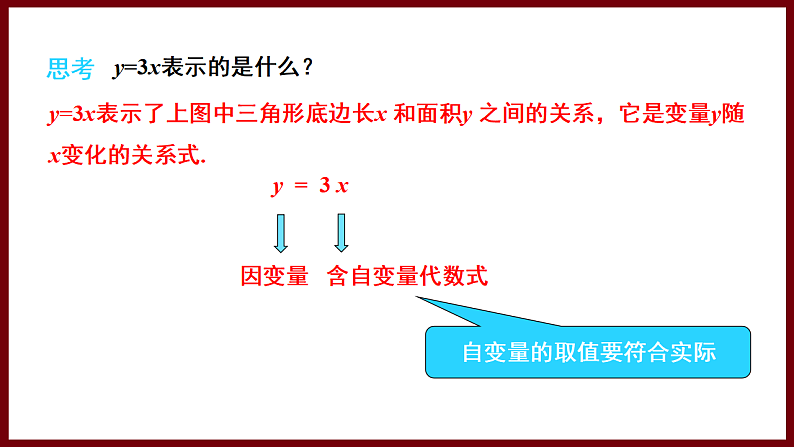
y=3x表示的是什么？
自变量的取值要符合实际
y=3x表示了上图中三角形底边长x 和面积y 之间的关系，它是变量y随x变化的关系式.
关系式的定义：用来表示自变量和因变量之间关系的等式叫作关系式，利用关系式 (如y=3x)，我们可以根据任何一个自变量的值求出相应的因变量的值.
①等式的左边是因变量，等式的右边是关于自变量的代数式；②等式中只含有自变量和因变量这两个变量，其他的量都是常量；③自变量可在允许的范围内任意取值．
你还记得圆锥的体积公式是什么吗？其中的字母表示什么？
r指的是底面圆的半径，h指的是圆锥的高.
如图，圆锥的高是4 cm，当圆锥的底面半径由小到大变化时，圆锥的体积也随之发生了变化.(1)在这个变化过程中，自变量、因变量各是什么？底面半径增大时，圆锥的体积是如何变化的？圆锥的底面半径的长度是自变量；圆锥的体积是因变量；圆锥的底面半径增大，圆锥的体积也随之增大.
(3)当底面半径由1 cm变化到10 cm时，圆锥的体积由 cm3变化到 　　　 cm3 .
(2)如果圆锥底面半径为 r (cm)，那么圆锥的体积V (cm3)与 r 的关系式为________.
你知道什么是“低碳生活”吗？“低碳生活”是指人们尽量减少所耗能量，从而降低碳(特别是二氧化碳)的排放量的一种生活方式.
(2)随着耗电量的增加，二氧化碳排放量是如何变化的? 与同伴进行交流.
随着耗电量的增加，二氧化碳排放量也随之增加.
(3)当耗电量为 100 kW·h 时，二氧化碳排放量是多少?
当x=100时，y=100×0.785=78.5， 所以二氧化碳排放量是78.5 kg.
(1)你能用字母表示家居用电的二氧化碳排放量的公式吗? 其中的字母表示什么?
y=0.785x，其中x是耗电量，y是二氧化碳排放量.
(4)小明家本月大约用电 110 kW·h、耗油 75 L、用天然气 20 m3、用自来水 5 m3，请你计算小明家这几项的二氧化碳排放量总和.
家居用电的二氧化碳：110×0.785=86.35(kg)
开私家车的二氧化碳：75×2.7=202.5(kg)
家用天然气的二氧化碳：20×0.19=3.8(kg)
家用自来水的二氧化碳：5×0.91=4.55(kg)
二氧化碳排放量总和=86.35+202.5+3.8+4.55=297.2(kg)
1.一粒石子落入湖面，形成一个如圆周样的涟漪，在圆周长C与半径r的关系式C=2πr中，变量是( )
A. C，rB. C，πC. π，rD. C，2π
2.(2024广西)激光测距仪L 发出的激光束以3×105km/s的速度射向目标M，t s后测距仪L 收到M 反射回的激光束. 则L 到M 的距离d km与时间t s的关系式为( )
A. d= B. d=3×105tC. d=2×3×105tD. d=3x106t
3.(2024甘肃)如图1，“燕几”即宴几，是世界上最早的一套组合桌，由北宋进士黄伯思设计.全套“燕几”一共有七张桌子，包括两张长桌、两张中桌和三张小桌，每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图2给出了《燕几图》中名称为“回文”的桌面拼合方式，若设每张桌面的宽为x尺，长桌的长为y尺，则y与r的关系可以表示为( )
A. y=3x B. y=4xC. y=3x+1 D. y=4x+1
4. 根据图中的程序，当输入x＝3时，输出的结果 y＝ .
5.如图，圆柱的底面直径是2 cm，当圆柱的高h cm由大到小变化时，圆柱的体积V(cm3)随之发生变化.(1)在这个变化中，自变量和因变量各是什么？(2)写出圆柱的体积V与高h之间的关系式；
自变量是圆柱的高，因变量是圆柱的体积.
(3)当h由10 cm变化到5 cm时，V是怎样变化的？(4)当h=0时，V等于多少？此时表示什么？
当h=10 cm时，V=πh=10π cm3；当h=5 cm时，V=πh=5π cm3.所以当h 由10 cm变化到5 cm时，V从10π cm3变化到5π cm3.
V=0，此时表示平面图形——直径为2cm的圆.
用关系式表示变量之间的关系
利用关系式求因变量的值，实际上就是求代数式的值
关系式是用含自变量的代数式表示因变量的等式．
利用关系式表示变量之间的关系，最大的优点在于能比较方便地求出：自变量为取值范围内的任意一个值时，相对应的因变量的值．
知识点1　用关系式表示变量间的关系
1.波音777X型是新一代双引擎宽体客机，巡航速度为0.84马赫，约为286米/秒.若试飞过程中，飞行路程为y米，飞行时间为x秒，则y与x之间的关系式为 (　B　)
2. 某夏令营组织1名老师带若干名学生探索喀斯特地貌的溶洞.已知成人 票每人50元，学生票每人20元.设门票的总费用为y元，学生人数为x名， 则y与x的关系式为 (　A　)
3.1　将面积改为周长
已知一个等腰△ABC的周长为20 cm，其中底边长为x cm，腰长为y cm， 则y与x的关系式为(　D　)
3.2　改变因变量求关系式如图，在△ABC中，已知BC＝15，高AD＝8，动点P由点B沿BC向点C移 动.设BP的长为x(0＜x＜15)，△ACP的面积为S，则S与x之间的关系式 为 ⁠.
S＝－4x＋60(0＜x＜15)
知识点2　根据关系式求变量的值
4. (教材复习题第2题改编)如图，大拇指与小拇指张开时，两指尖的距离 称为“指距”.研究表明，人的身高h(单位：cm)与指距d(单位：cm)之间 满足关系式：h＝9d－20，若小新的指距为19 cm，则他的身高为(　D　)
5. 小颖发现，在一定范围内，尺码对照表中脚长y(单位：cm)与鞋码x(单 位：码)之间的换算公式为y＝(x＋10)÷2.若小颖脚长约为23.5 cm，则她 应穿的鞋码为(　C　)
6. (教材随堂练习第1题改编)血压是衡量心血管健康的重要指标，有研究 表明，一个成年女性正常的收缩压p(单位：毫米汞柱)与年龄x(单位：岁) 之间的关系可以近似表示为：p＝0.01x2＋0.05x＋107，在其上下20毫米 汞柱的范围浮动均属于正常收缩压.(1)上述变化关系中，自变量和因变量分别是什么？
解：自变量是年龄，因变量是收缩压；
(2)萧萧妈妈今年35岁，测得她的收缩压为119毫米汞柱，则她的收缩压在 正常区间吗？请说明理由.
解：她的收缩压在正常区间.理由如下：将x＝35带入p＝0.01x2＋0.05x＋107，得到p＝121，因为119在121上下20毫米汞柱的范围内，所以她的收缩压在正常区间.
7. 如图①，将一张边长为20 cm的大正方形纸片裁掉四个边长均为x cm的 小正方形(即阴影部分)，并折成如图②所示的无盖长方体盒子，则长方体 盒子的体积y(cm3)与小正方形的边长x(cm)之间的关系式是(　B　)
8. 如图是生活中常见的钟表.请写出时针从某天中午12时至晚上12时转过 的角度θ(°)与转动时间t(时)之间的关系式： (并写出 自变量的取值范围).
θ＝30t(0≤t≤12)
9. 漏刻是古代的一种计时工具，根据等时性原理滴水计时.小珍依据漏刻 的基本原理做出了如图所示的简易计时器.甲容器开始放水后每隔10 min 观察一次乙容器中的水面高度h，获得的数据大致如下表所示.
(1)上述过程中，自变量和因变量分别是什么？
解：自变量为流水时间，因变量为乙容器中的水面高 度；
(2)若乙容器的高度为30 cm，8：00开始放水，则乙容器内接满水时为 几点？
解：根据表格可知，每过10 min，乙容器中的水面高度升高2 cm，所以乙容器中的水面高度的变化速度为0.2 cm/min，因为乙容器中水面初始高度为3 cm，所以乙容器内水面高度h与流水时间t之间的关系式为h＝0.2t＋3，将h＝30代入关系式可得，30＝0.2t＋3，解得t＝135，因为135 min＝2 h15 min，所以8：00开始放水，乙容器内接满水时为10：15.
10. (项目式学习·数学与生活融合)根据以下素材，完成任务.
解：由题意可知，当双层部分的长度x每增加1 cm时，单肩包的
长度y减少1 cm，单肩包背带最长为150 cm，所以y与x之间的关系
式为y＝150－x(0≤x≤150)；