初中数学华东师大版（2024）八年级下册18.2 平行四边形的判定优秀课件ppt

这是一份初中数学华东师大版（2024）八年级下册18.2 平行四边形的判定优秀课件ppt，文件包含华师大版数学八年级下册1822《平行四边形的判定2》课件pptx、华师大版数学八年级下册1822《平行四边形的判定2》教案docx、华师大版数学八年级下册1822《平行四边形的判定2》学案doc等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。
1.掌握用“对角线互相平分的四边形是平行四边形”这一判 定定理． 2.利用平行四边形的判定进行简单的推理和证明．
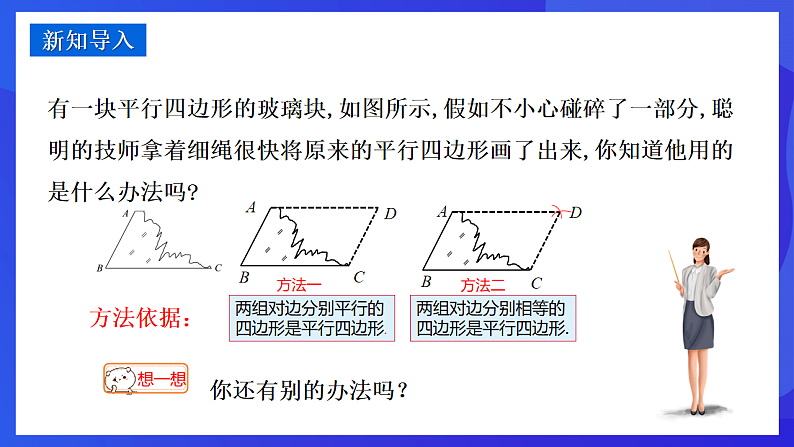
有一块平行四边形的玻璃块,如图所示,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么办法吗?
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
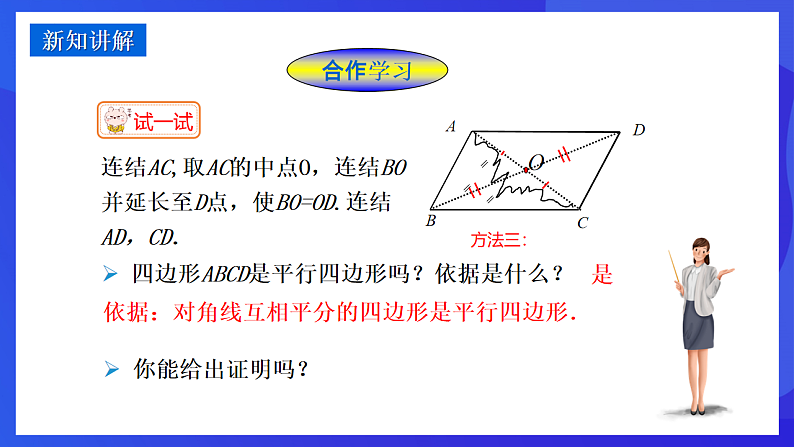
连结AC,取AC的中点O，连结BO并延长至D点，使BO=OD.连结AD，CD．
依据：对角线互相平分的四边形是平行四边形．
四边形ABCD是平行四边形吗？依据是什么？
某装饰店要招聘店员，老板出了这样一道考题：“一顾客要一块平行四边形的玻璃，你能否利用手头工具，一长一短的两根小木棒，画出一个平行四边形玻璃，并说明这块玻璃符合顾客要求的道理。”你能为招聘人员设计一方案吗？
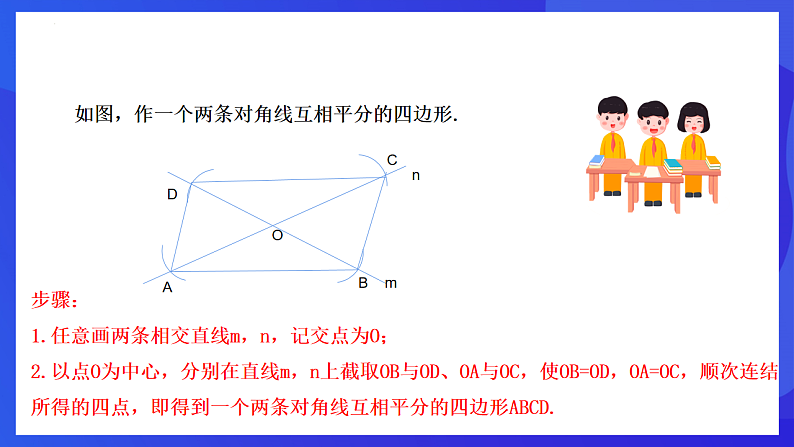
如图，作一个两条对角线互相平分的四边形.
步骤：1.任意画两条相交直线m，n，记交点为O；2.以点O为中心，分别在直线m，n上截取OB与OD、OA与OC，使OB=OD，OA=OC，顺次连结所得的四点，即得到一个两条对角线互相平分的四边形ABCD.
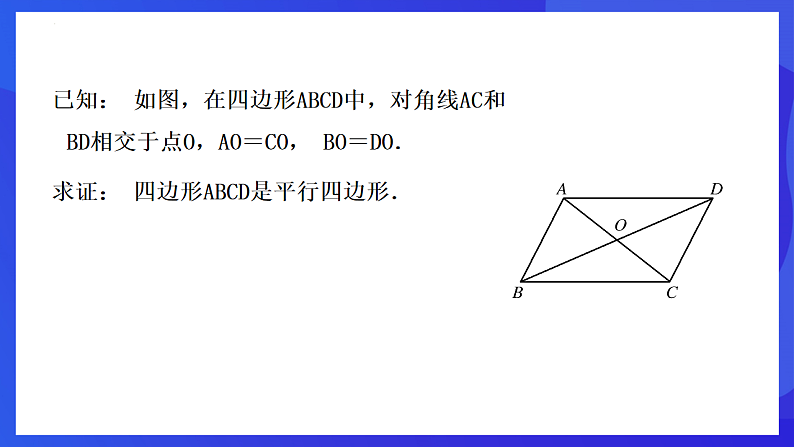
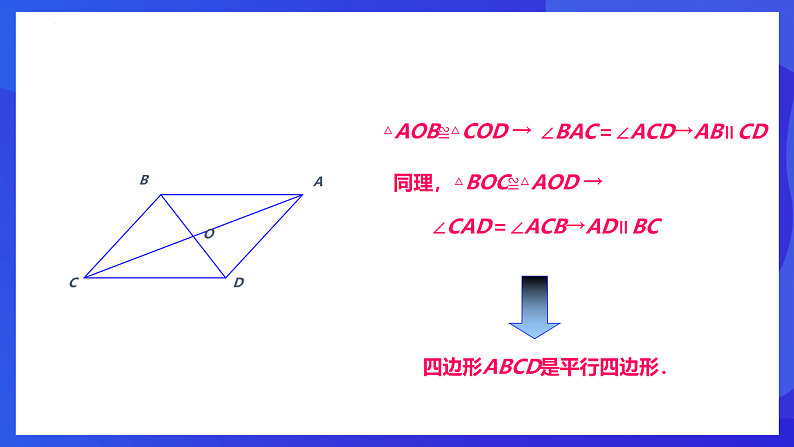
已知： 如图，在四边形ABCD中，对角线AC和BD相交于点O，AO＝CO， BO＝DO．求证： 四边形ABCD是平行四边形．
△AOB≌△COD →
∠BAC＝∠ACD→AB∥CD
∠CAD＝∠ACB→AD∥BC
同理，△BOC≌△AOD →
四边形ABCD是平行四边形．
判定定理四： 对角线互相平分的四边形是平行四边形．
∴ 四边形ABCD是平行四边形. （对角线互相平分的四边形是平行四边形）
∵ A0=C0, BO=DO
∵四边形ABCD是平行四边形 ∴ AO=CO，BO=DO ∵AE=CF ∴AO－AE=CO－CF ∴EO=FO 又 BO=DO ∴ 四边形BFDE是平行四边形
证明：连接对角线BD，交AC于点O
例2、已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF．求证：四边形BFDE是平行四边形．
∴△AED ≌△CFB(SAS)∴DE=BF同理可证：BE=DF四边形BFDE是平行四边形．
例3：如图，在□ABCD中，点F，H分别在边AB，CD上，且BF=DH.求证：AC和HF互相平分.
证明：连结AH、CF∵四边形ABCD是平行四边形∴AB//CD,AB=CD又∵BF=DH∴AB-BF=CD-DH即AF=CH∴四边形AFCH是平行四边形∴AC和HF互相平分
例4：如图，在四边形ABCD中，∠A=∠C，∠B=∠D.求证：四边形ABCD是平行四边形.
证明：在四边形ABCD中，∵∠A+∠B+∠C+∠D=360°且∠A=∠C，∠B=∠D∴∠A+∠B+∠A+∠B=360°即2（∠A+∠B）=360°∴∠A+∠B=180°∴AD//CB.同理可证：AB//CD∴四边形ABCD是平行四边形.
通过这个题目，你有什么发现？
例5、四边形AEFD和EBCF都是平行四边形，求证四边形ABCD是平行四边形.
证明：∵四边形AEFD是平行四边形∴AD∥EF，AD=EF
又∵四边形EBCF是平行四边形∴EF∥BC,EF=BC
∴AD∥BC,AD=BC
∴四边形ABCD是平行四边形.
例6、如图，G、H是□ABCD对角线AC上的两点，且AG=CH，E，F分别是边AB和CD的中点.求证：四边形EHFG是平行四边形.
证明：连接EF交AC于点O∵四边形ABCD是平行四边形∴AB∥CD,AB=CD又∵E,F是AB,CD的中点。∴AE=CF又∵ AB∥CD,∠EAO=∠FCO在△EAO与△COF中
∵∠EAO=∠FCO∠AOE=∠COFAE=CF∴△AOE≌△COF∴OE=OF，OA=OC又∵AC=CH∴OC=OH∴四边形EHFG是平行四边形(对角线互相平分的四边形是平行四边形)
1.两组对边分别平行的四边形是平行四边形（定义）
2.两组对边分别相等的四边形是平行四边形 （判定定理1）
3.一组对边平行且相等相等的四边形是平行四边形 （判定定理2）
4.对角线互相平分的四边形是平行四边形 （判定定理3）
1.根据下列条件,不能判定四边形为平行四边形的是( ) A.两组对边分别相等 B.两条对角线互相平分C.两条对角线相等 D.两组对边分别平行
2.如图，线段AB，CD相交于点O，且图上各点把线段AB，CD四等分，这些点可以构成______个平行四边形．
3.如图，在平行四边形ABCD中，已知AE、CF分别是∠DAB、∠BCD的角平分线．证明：四边形AFCE是平行四边形．
判定一个四边形是平行四边形的方法：
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
4.两组对角分别相等的四边形是平行四边形.
5.对角线互相平分的四边形是平行四边形
1．如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是( )A．AB∥CD，∠DAO＝∠BCO B．AB∥CD，∠BAO＝∠DCOC．AO＝CO，BO＝DO D．AB＝CD，∠BAO＝∠DCO
2．如图，在四边形ABCD中，AC与BD相交于点O，AB∥CD，OA＝OC.求证：四边形ABCD是平行四边形．
证明：∵AB∥CD，∴∠ABO＝∠CDO，∠BAO＝∠DCO.又∵OA＝OC，∴△AOB≌△COD，∴OB＝OD.又∵OA＝OC，∴四边形ABCD为平行四边形．
3.如图，AB、CD相交于点O，AC∥DB，AO＝BO，E、F分别是OC、OD的中点．求证：(1)△AOC≌△BOD；(2)四边形AFBE是平行四边形．
证明：(1)∵AC∥BD，∴∠C＝∠D.又∵∠COA=∠DOB，AO＝BO ，∴△AOC≌△BOD(AAS)；(2)∵△AOC≌△BOD，∴CO＝DO.∵E、F分别是OC、OD的中点，∴EO＝FO.又∵AO＝BO，∴四边形AFBE是平行四边形．