九年级下册33.2 相似三角形精品ppt课件

这是一份九年级下册33.2 相似三角形精品ppt课件，共23页。PPT课件主要包含了学习目标，复习引入，△ADC，互动新授，不一定相似，典例精析，小试牛刀，课堂检测，拓展训练，课堂小结等内容，欢迎下载使用。
1.探索“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定定理.2.能够运用三角形相似的条件解决简单的问题.
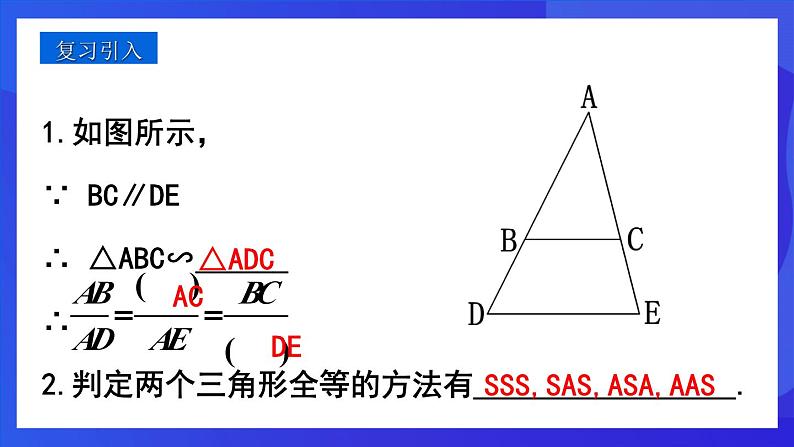
1.如图所示，∵ BC∥DE ∴ △ABC∽______ ∴ 2.判定两个三角形全等的方法有_________________.
SSS,SAS,ASA,AAS
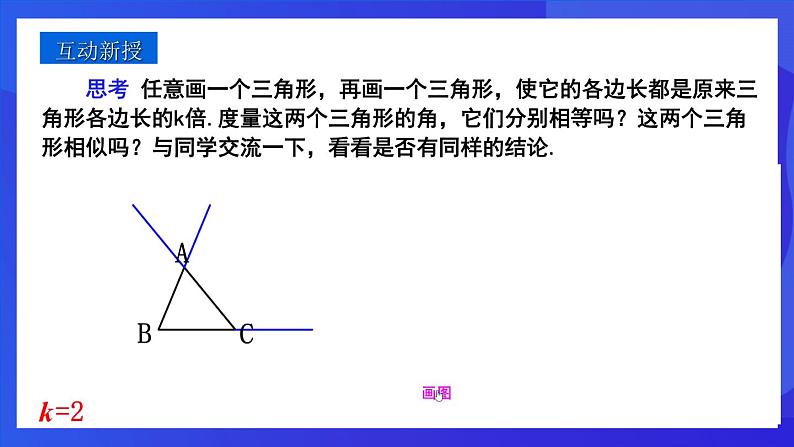
思考 任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍.度量这两个三角形的角，它们分别相等吗？这两个三角形相似吗？与同学交流一下，看看是否有同样的结论.
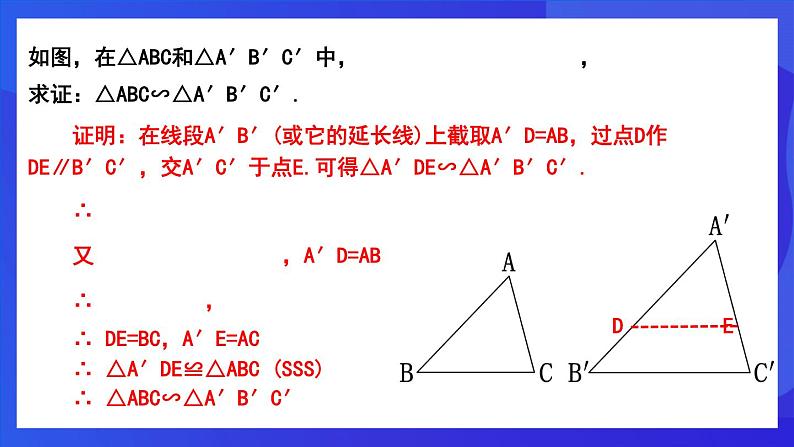
证明：在线段A′B′(或它的延长线)上截取A′D=AB，过点D作DE∥B′C′，交A′C′于点E.可得△A′DE∽△A′B′C′. ∴ 又 ，A′D=AB ∴ ， ∴ DE=BC，A′E=AC ∴ △A′DE≌△ABC (SSS) ∴ △ABC∽△A′B′C′
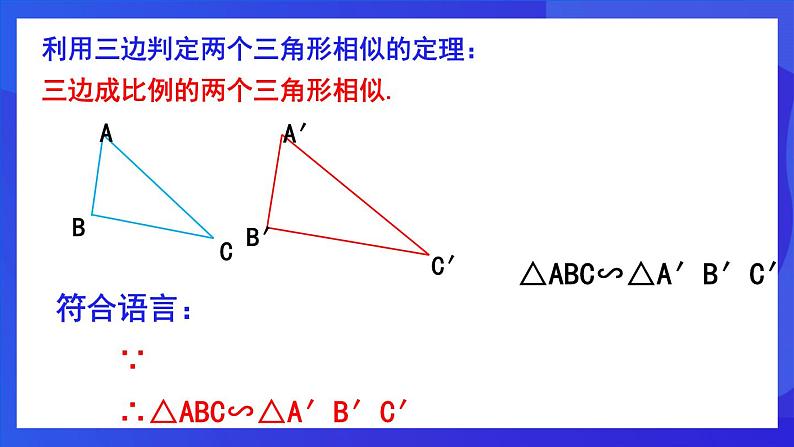
利用三边判定两个三角形相似的定理：三边成比例的两个三角形相似.
△ABC∽△A′B′C′
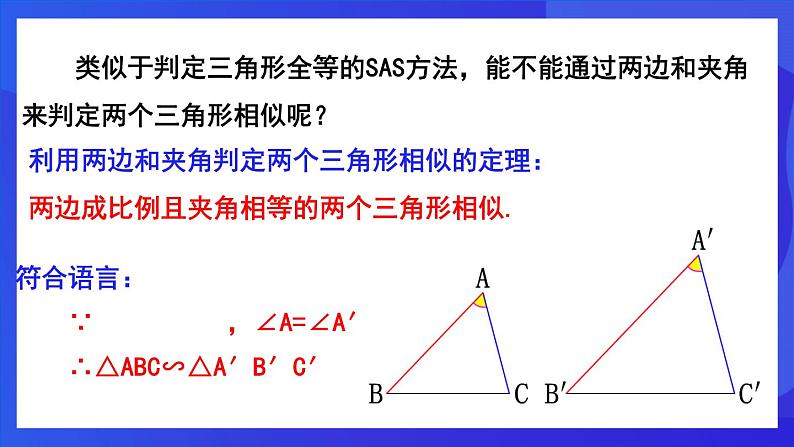
类似于判定三角形全等的SAS方法，能不能通过两边和夹角来判定两个三角形相似呢？
利用两边和夹角判定两个三角形相似的定理：两边成比例且夹角相等的两个三角形相似.
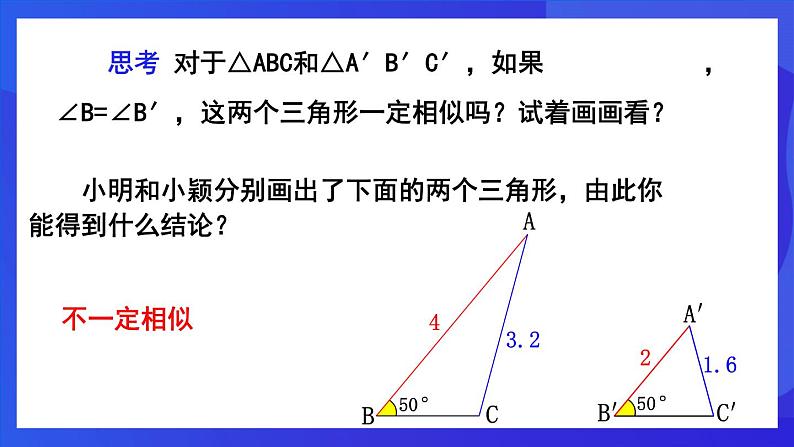
小明和小颖分别画出了下面的两个三角形，由此你能得到什么结论？
例1 根据下列条件，判断△ABC和△A′B′C′是否相似，并说明理由： (1)AB=4cm，BC=6cm，AC=8cm，A′B′=12cm，B′C′=18cm，A′C′=24cm； (2)∠A=120°，AB=7cm，AC=14cm，∠A′=120°，A′B′=3cm，A′C′=6cm.
解：(1)∵ ， ， . ∴ ∴ △ABC∽△A′B′C′
解：(2)∵ ， . ∴ 又∠A=∠A′ ∴△ABC∽△A′B′C′
例1 根据下列条件，判断△ABC和△A′B′C′是否相似，并说明理由： (2)∠A=120°，AB=7cm，AC=14cm，∠A′=120°，A′B′=3cm，A′C′=6cm.
1.若△ABC的每条边长增加各自的10%得△A′B′C′，则∠B′的度数与其对应角∠B 的度数相比(　　) A．增加了10% B．减少了10% C．增加了(1＋10%) D．没有改变
1.如图，4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC 相似的三角形所在的网格图形是(　　)
1.如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3，4及x，那么x 的值(　　) A．只有1个 B．有2个 C．有3个 D．有无数个
5.如图，在△ABC中，AB＝AC＝1，BC＝　　 ，在AC 边上截取AD＝BC，连接BD.(1)通过计算，判断AD2与AC·CD 的大小关系；(2)求∠ABD 的度数．
(1)通过计算，判断AD2与AC·CD 的大小关系；
(2)求∠ABD 的度数．
1.如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形.若OA_OBOCOD，则下列结论中一定正确的是( ) A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似
解：∵ AE=1.5，AC=2，
∵∠EAD=∠CAB，∴ △ADE∽△ABC，