初中数学33.2 相似三角形完整版课件ppt

这是一份初中数学33.2 相似三角形完整版课件ppt，共21页。PPT课件主要包含了学习目标，复习引入，合作探究，总结归纳，典例精析，小试牛刀，课堂检测，拓展训练，课堂小结，课后作业等内容，欢迎下载使用。
1.了解“两角分别相等的两个三角形相似”和“如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似.”判定定理的证明过程，能运用这两个判定定理证明两个三角形相似.2.通过对相似三角形两个判定定理的学习，会用已知条件证明三角形相似并解决一些简单的问题.
如何判断两个三角形是否相似呢？1.定义法:对应角相等，对应边成比例的两个三角形相似.2.平行于三角形一边的直线和其他两边(或两边的延长线）相交，所构成的三角形与原三角形相似.3.三边成比例的两个三角形相似.4.两边成比例且夹角相等的两个三角形相似.
问1 度量 AB，BC，AC，A′B′，B′C′，A′C′ 的长，并计算出它们的比值. 你有什么发现？
与同伴合作，一人画 △ABC，另一人画 △A′B′C′，使∠A=∠A′=40°，∠B=∠B′=55°，探究下列问题：
这两个三角形是相似的
问2 试证明△ABC∽△A′B′C′.
证明：在△A′B′C′的边A′B′上，截取 A′D=AB，过点 D 作 DE // B′C′，交 A′C′ 于点 E，则有△A′DE ∽△A′B′C′，∠A′DE =∠B′.∵∠B=∠B′，∴∠A′DE=∠B.∵ A′D=AB，∠A=∠A′，∴△A′DE ≌△ABC，∴△ABC∽△A′B′C′.
利用两组角判定两个三角形相似的定理：两角分别相等的两个三角形相似.
符合语言： ∵∠A=∠A'，∠B=∠B'， ∴△ABC∽△A′B′C′.
例2 如图，在 Rt△ABC 中，∠C=90°，AB=10，AC=8. E是AC上一点，AE=5，ED⊥AB，垂足为D.求AD的长.
由三角形相似的条件可知，如果两个直角三角形满足一个锐角相等，或两组直角边成比例，那么这两个直角三角形相似.
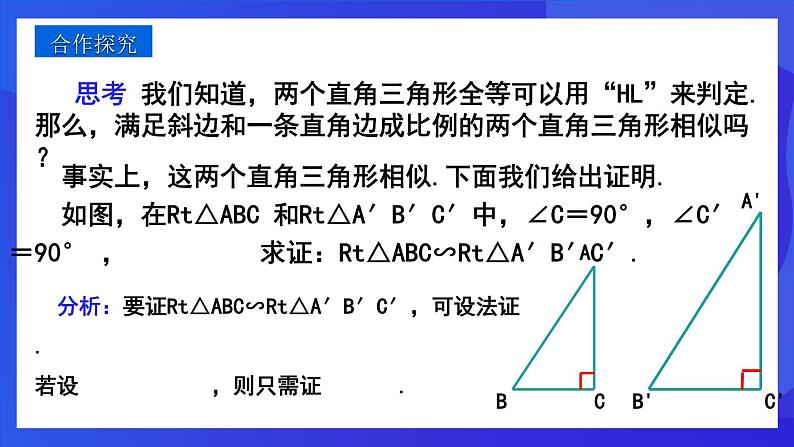
思考 我们知道，两个直角三角形全等可以用“HL”来判定.那么，满足斜边和一条直角边成比例的两个直角三角形相似吗？
证明：设 ，则AB=kA′B′，AC=kA′C′.由勾股定理，得 ， ∴ .∴ ∴ Rt△ABC∽Rt△A′B′C′
由此得到另一个判定直角三角形相似的方法：斜边和一直角边成比例的两个直角三角形相似.
符合语言： ∵∠C=∠C′=90°， ∴Rt△ABC∽Rt△A′B′C ′.
1.下列各组条件中，不能判定△ABC与△A′B′C′相似的是(　　) A.∠A＝∠A′，∠B＝∠B′ B.∠C＝∠C′＝90°，∠A＝35°，∠B′＝55° C.∠A＝∠B，∠A′＝∠B′ D.∠A＋∠B＝∠A′＋∠B ′,∠A－∠B＝∠A′－∠B ′
2.如图，在 Rt△ABC 中， ∠ABC=90°，BD⊥AC于D.若AB=6，AD=2，则 AC= ，BD= ，BC= .
1.如图，△ABC 中，∠A＝78°，AB＝4，AC＝6.将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是(　　)
2.如图，△ABC 中，DE∥BC，EF∥AB，求证：△ADE∽△EFC.
证明:∵DE∥BC，EF∥AB， ∴∠AED＝∠C，∠A＝∠FEC. ∴ △ADE∽△EFC.
3.如图，D是△ABC的边AB上一点，连接CD.若AD=2,BD=4，∠ACD=∠B，求AC的长.
解:∵AD=2,BD=4 ∴AB=2+4=6 ∵∠ACD=∠B 又∠A=∠A ∴△ACD∽△ABC ∴ ∴AC2=12，解得，AC=
1.如图，⊙O 的弦 AB，CD 相交于点P，若 PA=3，PB=8，PC=4，则PD= .
2.弦AB 和CD 相交于⊙O内一点P,求证:PA·PB=PC·PD.
证明:连接AC、BD ∵∠A、∠D都是弧CB所对的圆周角 ∴∠A=∠D 同理: ∠C=∠B ∴△PAC∽△PDB ∴ ∴PA·PB=PC·PD.
1.如图，已知 AB∥DE，∠AFC ＝∠E，则图中相似三角形共有( ) A. 1对 　　B. 2对 C. 3对 　　D. 4对
证明：(1)∵CD 是斜边AB上的高，∴∠ADC＝90°. 在Rt△ABC 中，∠ACB＝90°， ∴∠ADC＝∠ACB. 又∵∠A＝∠A，∴△ACD∽△ABC. (2)∵CD 是斜边AB上的高， ∴∠CDB＝90°. 在Rt△ABC 中，∠ACB＝90°， ∴∠CDB＝∠ACB. 又∵∠B＝∠B，∴△CBD∽△ABC.
2.如图，Rt△ABC 中，CD 是斜边AB上的高.求证：(1)△ACD∽△ABC； (2)△CBD∽△ABC.