北师大版（2024）七年级下册（2024）3 探究三角形全等的条件课文ppt课件

这是一份北师大版（2024）七年级下册（2024）3 探究三角形全等的条件课文ppt课件，共34页。PPT课件主要包含了DEEF，基础题，第3题图，AC＝DE，AB＝DB，综合题，拓展提升，图①第12题图等内容，欢迎下载使用。
1. 熟练掌握三角形全等的 4 种判定方法.2. 能结合其他知识灵活运用三角形全等的判定方法解决问题.
判定三角形全等的方法有哪些？
(1) 三边分别相等的两个三角形全等；(2) 两角及其夹边分别相等的两个三角形全等；(3) 两角分别相等且其中一组等角的对边相等的两个三角形全等；(4) 两边及其夹角分别相等的两个三角形全等.
让我们用这几个判定方法来解决问题吧！
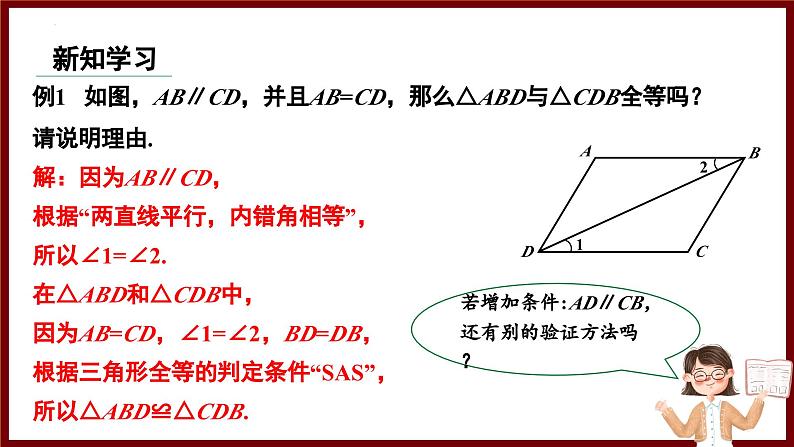
例1 如图，AB∥CD，并且AB=CD，那么△ABD与△CDB全等吗？请说明理由.
解：因为AB∥CD，根据“两直线平行，内错角相等”，所以∠1=∠2.在△ABD和△CDB中，因为AB=CD，∠1=∠2，BD=DB，根据三角形全等的判定条件“SAS”，所以△ABD≌△CDB.
若增加条件:AD∥CB，还有别的验证方法吗？
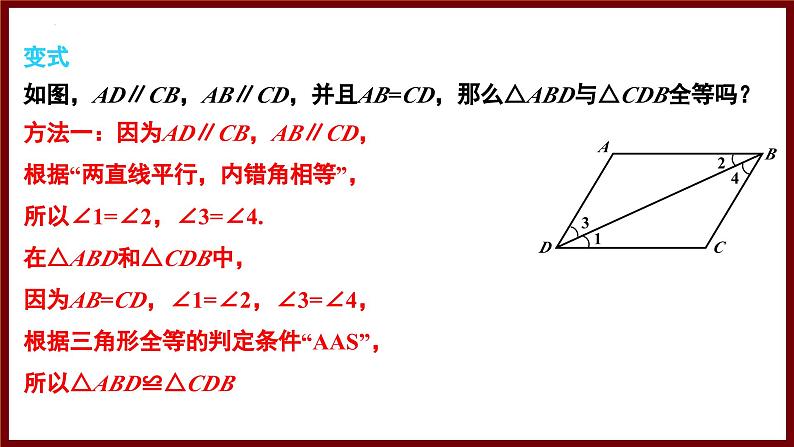
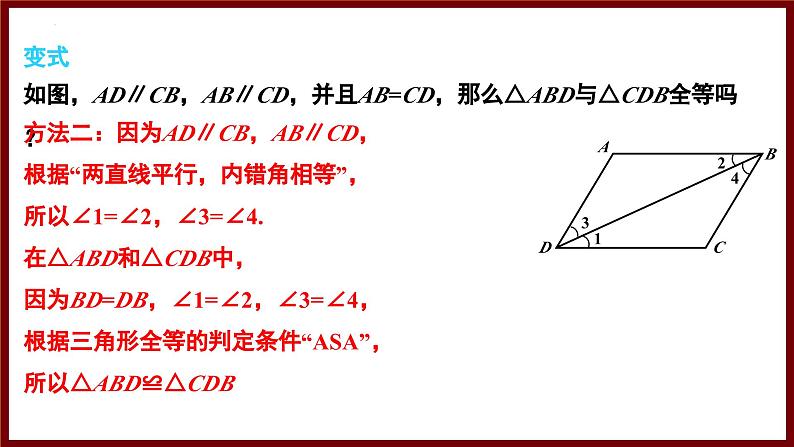
如图，AD∥CB，AB∥CD，并且AB=CD，那么△ABD与△CDB全等吗？
方法一：因为AD∥CB，AB∥CD，根据“两直线平行，内错角相等”，所以∠1=∠2，∠3=∠4.在△ABD和△CDB中，因为AB=CD，∠1=∠2，∠3=∠4，根据三角形全等的判定条件“AAS”，所以△ABD≌△CDB
方法二：因为AD∥CB，AB∥CD，根据“两直线平行，内错角相等”，所以∠1=∠2，∠3=∠4.在△ABD和△CDB中，因为BD=DB，∠1=∠2，∠3=∠4，根据三角形全等的判定条件“ASA”，所以△ABD≌△CDB
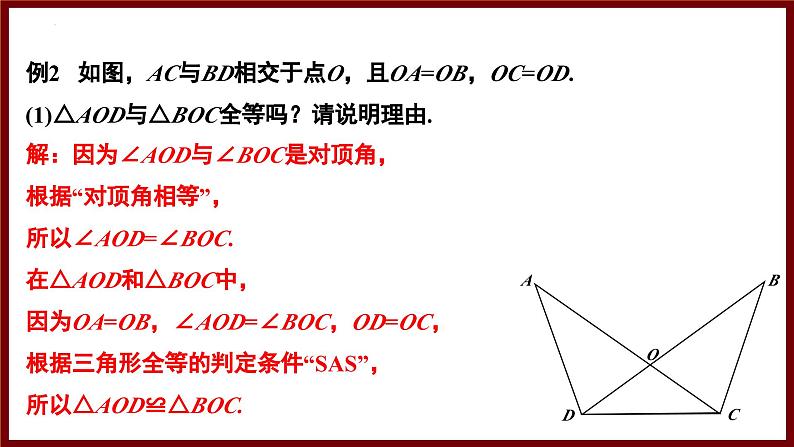
解：因为∠AOD与∠BOC是对顶角，根据“对顶角相等”，所以∠AOD=∠BOC.在△AOD和△BOC中，因为OA=OB，∠AOD=∠BOC，OD=OC，根据三角形全等的判定条件“SAS”，所以△AOD≌△BOC.
例2 如图，AC与BD相交于点O，且OA=OB，OC=OD.(1)△AOD与△BOC全等吗？请说明理由.
例2 如图，AC与BD相交于点O，且OA=OB，OC=OD.(2)△ACD与△BDC全等吗？为什么？
解：由(1)可知，△AOD≌△BOC，根据“全等三角形的对应边相等”，所以AD=BC.因为OA=OB，OC=OD，AC=OA+OC，BD=OB+OD. 所以AC=BD.在△ACD和△BDC中，因为AD=BC，AC=BD，DC=CD，根据三角形全等的判定条件“SSS”，所以△ACD≌△BDC.
你还能根据其他的判定条件，判断这两个三角形全等吗？
方法二：由(1)可知，△AOD≌△BOC，根据“全等三角形的对应边相等，对应角相等”，所以AD=BC，∠A=∠B.因为OA=OB，OC=OD，AC=OA+OC，BD=OB+OD. 所以AC=BD.在△ACD和△BDC中，因为AD=BC，AC=BD，∠A=∠B，根据三角形全等的判定条件“SAS”，所以△ACD≌△BDC.
SAS或ASA或AAS
1. 如图，△ABC中，∠B=∠C，BD=CF，BE=CD，∠EDF=α，则下列结论正确的是( )A．2α+∠A=180° B．α+∠A=90° C．2α+∠A=90° D．α+∠A=180°
2. (2024牡丹江)如图，△ABC中，D是AB上一点，CF∥AB，D、E、F三点共线，请添加一个条件 ，使得AE=CE.(只添一种情况即可)
3. 如图 AE=CF，∠AFD=∠CEB，DF=BE，△AFD与△CEB全等吗？为什么？
解：全等，理由如下：因为AE=CF，所以AE－FE=CF－EF，即 AF=CE.在△AFD和△CEB中，AF=CE，∠AFD=∠CEB，DF=BE.根据三角形全等的判定条件“SAS”，所以△AFD≌△CEB.
4. (2024长沙节选)如图，点C在线段AD上，AB=AD，∠B=∠D，BC=DE.试说明: △ABC≌△ADE；
解：在△ABC和△ADE中，BC=DE，∠B=∠D，AB=AD，根据三角形全等的判定条件“SAS”，所以△ABC≌△ADE.
解：因为点D为BC边的中点，所以BD=CD，因为BE∥AC，所以∠EBD=∠C，∠E=∠CAD，在△BDE和△CDA中，∠EBD=∠C，∠E=∠CAD，BD=CD.根据三角形全等的判定条件“AAS”所以△BDE≌△CDA.
5. (2024南充)如图，在△ABC中，点D为BC边的中点，过点B作BE∥AC交AD的延长线于点E.(1)试说明：△BDE≌△CDA.
5. (2024南充)如图，在△ABC中，点D为BC边的中点，过点B作BE∥AC交AD的延长线于点E.(2)若AD⊥BC，试说明：BA=BE.
解：因为点D为BC边的中点，所以BD=CD又因为AD⊥BC，所以∠ADB=∠ADC在△ABD和△ACD中，AD=AD，∠ADB=∠ADC，BD=CD.根据三角形全等的判定条件“SAS”所以△ABD≌△ACD.
所以BA=CA由(1)得△BDE≌△CDA，所以BE=CA，所以BA=BE.
知识点　灵活运用全等三角形的判定方法
1. 如图，在△ABC中，D，E为BC边上两点，AB＝AC，添加下列条件 不．能．判定△ABE≌△ACD的是(　B　)
第1题图
2. 如图，将长方形纸片ABCD沿对角线AC折叠后，点D落在点E处，与BC 交于点F，图中全等三角形(包含△ADC)对数有(　D　)
3. 如图，A，D，B，E四点在同一条直线上，AD＝BE，AC∥DF，AC＝ DF，CD为∠ACB的平分线，已知∠A＝28°，∠E＝76°，则∠DCB的度 数为(　C　)
4. (中考新考法·添加条件开放)如图，在△ABC和△DBE中，BC与DE交于 点F，若BC＝BE，还需添加两个条件 ________ 、 _________，使得△ABC≌△DBE，则判定全等的依据是 ___________________ (填简写)．
SSS（答案不唯一）
5. 如图，在△ABC中，AD平分∠BAC交BC于点D，点E是AB边上一点， 且AE＝AC，连接DE，若BC＝5，DE＝2，则BD的长度为 _____．
6. (教材习题第16题改编)如图，已知△ABC.
(1)利用尺规作出△DEF，使得△DEF≌△ABC(不写作法，保留作图痕 迹)；
(2)根据(1)中作图过程写出△DEF≌△ABC的依据为 __________________．
7. 如图，在△ABC中，AD是BC边上的高，BE是AC边上的高，且AD，BE 交于点O，BO＝AC，试说明：△BDO≌△ADC.
8. 在△ABC中，已知∠B＝∠C＝40°，将△ABC沿图中虚线剪开，剪下 的两个三角形不．一．定．全等的是(　D　)
9. 如图，在△ABC中，CD平分∠ACB，AD⊥CD于点D，连接BD，若 S△ABC＝12，则阴影部分的面积为(　C　)
10. 如图，在△ABC和△ADE中，∠BAC＝∠DAE，AB＝AC，AD＝AE， 且AB＞AD，连接BE，CD交于点P，若∠AEB＝25°，∠CAD＝140°， 则∠ACD的度数为 ______．
11. 如图是某歌剧院的侧面结构简图，已知舞台AB与看台CD之间的距离为15 m，舞台AB的高度为1 m，为了增强观众的视觉体验，负责人在点P处安装了一个聚光灯，若AE⊥CD于点E，MN与地面平行，∠MPA＋∠DAE＝90°，且点A到点P的距离与点A到点D的距离相等，求此时点P处的聚光灯距离地面BC的高度．
解：如解图，过点P作PF⊥BC于点F，交AE于点G，
因为AE⊥CD，PF⊥BC，MN∥AE，
所以∠AED＝∠AGP＝∠MPF＝90°，GF＝AB，
由题意得，∠MPA＋∠DAE＝90°，∠MPA＋∠APF＝90°，AP＝DA，
所以∠APG＝∠DAE，
所以点P处的聚光灯距离地面BC的高度为16 m.
所以PF＝PG＋GF＝15＋1＝16 m，
所以△APG≌△DAE（AAS），
所以PG＝AE＝15 m，
12. (综合与实践·操作探究)根据问题情境探究图形，完成下列任务．
解：任务一：由题意可知AE＝DB，所以AE＋AD＝DB＋AD，所以DE＝AB，