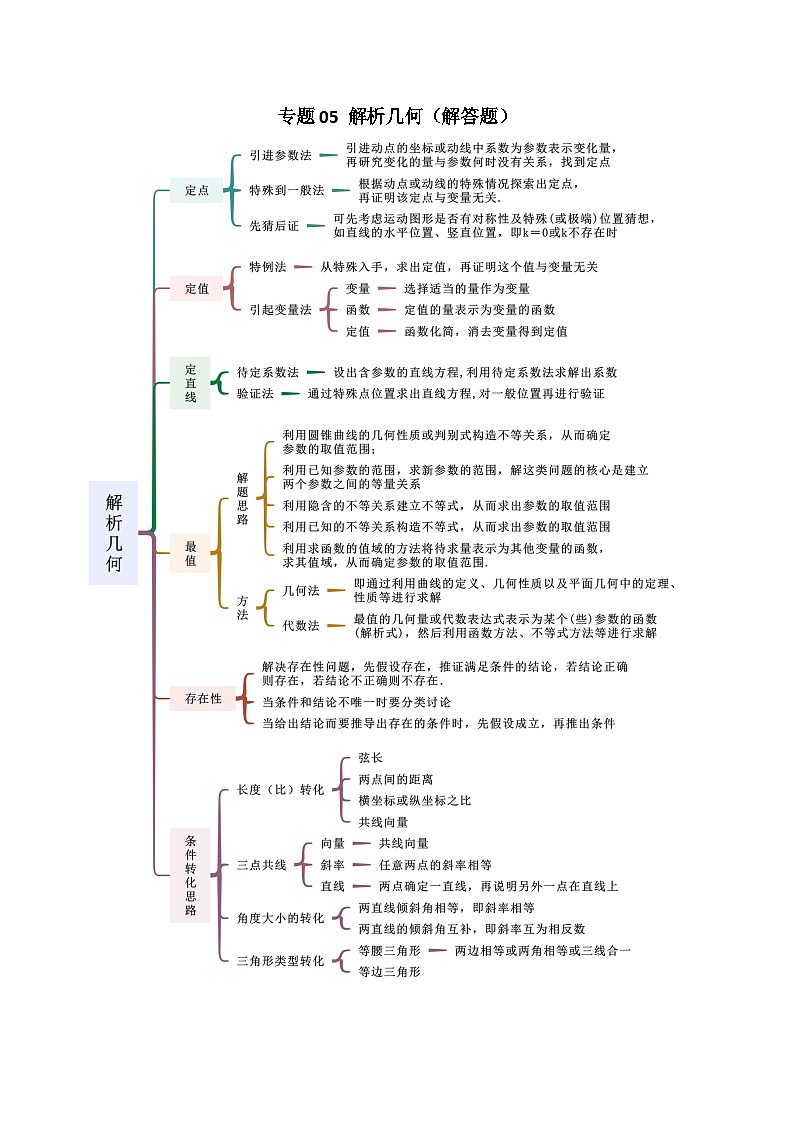
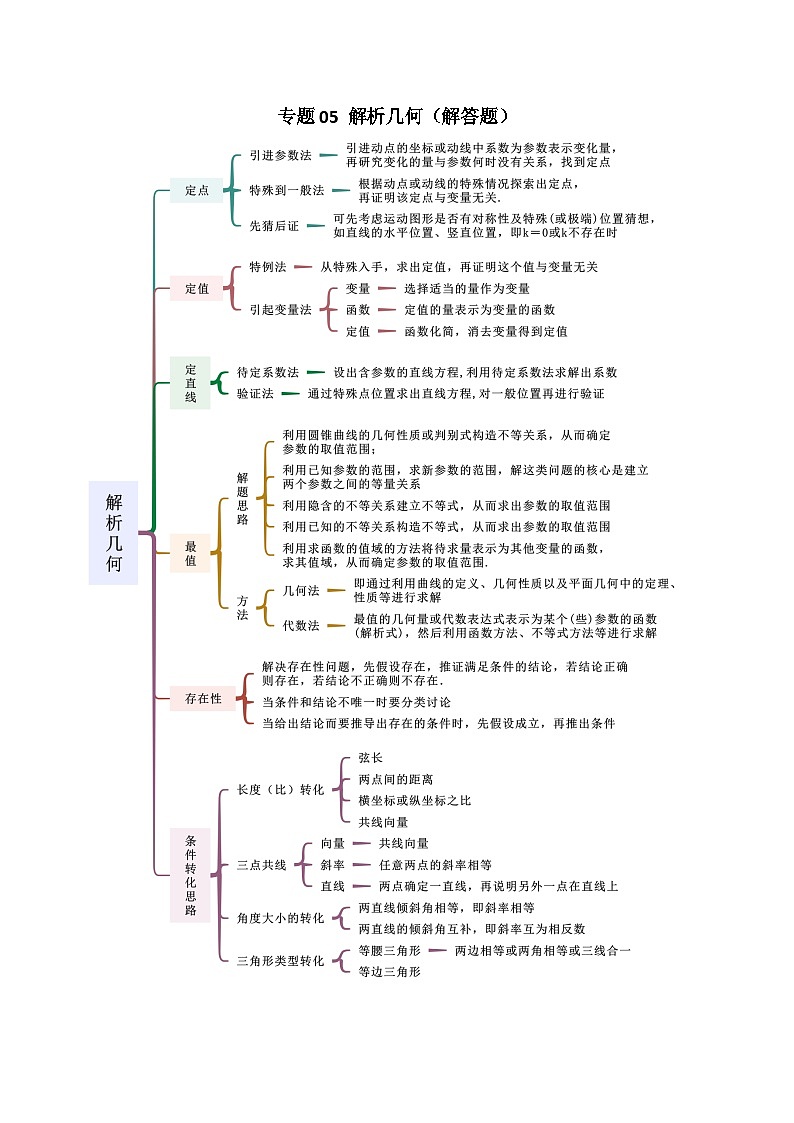
新高考数学二轮复习 专题05 解析几何 解答题题型分类提升讲与练（2份，原卷版+教师版）

这是一份新高考数学二轮复习 专题05 解析几何 解答题题型分类提升讲与练（2份，原卷版+教师版），文件包含新高考数学二轮复习专题05解析几何解答题题型分类提升讲与练教师版docx、新高考数学二轮复习专题05解析几何解答题题型分类提升讲与练原卷版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

考法一 定点
【例1】（2023·山西运城·山西省运城中学校校考二模）已知点为双曲线上一点，的左焦点到一条渐近线的距离为.
(1)求双曲线的标准方程；
(2)不过点的直线与双曲线交于两点，若直线PA，PB的斜率和为1，证明：直线过定点，并求该定点的坐标.
【变式】
1．（2022·全国·统考高考真题）已知椭圆E的中心为坐标原点，对称轴为x轴、y轴，且过两点．
(1)求E的方程；
(2)设过点的直线交E于M，N两点，过M且平行于x轴的直线与线段AB交于点T，点H满足．证明：直线HN过定点．
考法二 定值
【例2】（2023·四川南充·四川省南充高级中学校考三模）已知椭圆的左、右焦点为，，离心率为．点P是椭圆C上不同于顶点的任意一点，射线、分别与椭圆C交于点A、B，的周长为8．
(1)求椭圆C的标准方程；
(2)若，，求证：为定值．
【变式】
1．（2023·河北保定·统考二模）已知椭圆的中心在原点，焦点在轴上，长轴长为短轴长的2倍，若椭圆经过点，
(1)求椭圆的方程；
(2)若是椭圆上不同于点的两个动点，直线与轴围成底边在轴上的等腰三角形，证明：直线的斜率为定值．
考法三 定直线
【例3】（2023·全国·统考高考真题）已知双曲线C的中心为坐标原点，左焦点为，离心率为．
(1)求C的方程；
(2)记C的左、右顶点分别为，，过点的直线与C的左支交于M，N两点，M在第二象限，直线与交于点P．证明:点在定直线上.
【变式】
1．（2023·湖南永州·统考一模）已知点A为圆上任意一点，点的坐标为，线段的垂直平分线与直线交于点．
(1)求点的轨迹的方程；
(2)设轨迹E与轴分别交于两点（在的左侧），过的直线与轨迹交于两点，直线与直线的交于，证明：在定直线上．
考法四 最值
【例4】（2023·全国·统考高考真题）已知直线与抛物线交于两点，且．
(1)求；
(2)设F为C的焦点，M，N为C上两点，，求面积的最小值．
【变式】
1．（2023·浙江·模拟预测）我国著名数学家华罗庚曾说：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休.”事实上，很多代数问题可以转化为几何问题加以解决，已知曲线C上任意一点满足.
(1)化简曲线的方程；
(2)已知圆（为坐标原点），直线经过点且与圆相切，过点A作直线的垂线，交于两点，求面积的最小值.
考法五 轨迹问题
【例5】（2023·湖南·校联考二模）已知为双曲线的左右焦点，且该双曲线离心率小于等于，点和是双曲线上关于轴对称非重合的两个动点，为双曲线左右顶点，恒成立．
(1)求该双曲线的标准方程；
(2)设直线和的交点为，求点的轨迹方程．
【变式】
1．（2023·湖南长沙·雅礼中学校考一模）已知椭圆C：，直线l与椭圆C交于A，B两点．
(1)点为椭圆C上的动点（与点A，B不重合），若直线PA，直线PB的斜率存在且斜率之积为，试探究直线l是否过定点，并说明理由；
(2)若．过点O作，垂足为点Q，求点Q的轨迹方程．
考法六 三角形类型的转化
【例6】（2022·黑龙江佳木斯·佳木斯一中校考三模）已知椭圆，左焦点为，上顶点为，直线BF与椭圆交于另一点Q，且，且点在椭圆上.
(1)求椭圆C的方程；
(2)设，，M是椭圆C上一点，且不与顶点重合，若直线与直线交于点P，直线与直线交于点.证明：是等腰三角形.
【变式】
1.（2022·浙江·模拟预测）已知直线l：为双曲线C：的一条渐近线，且双曲线C经过点.
(1)求双曲线C的方程；
(2)设A，B是双曲线右支上两点，若直线l上存在点P，使得为正三角形，求直线AB的斜率的取值范围.
专题05 解析几何（解答题） 巩固提升练习
1.（2023·全国·统考高考真题）已知椭圆的离心率是，点在上．
(1)求的方程；
(2)过点的直线交于两点，直线与轴的交点分别为，证明：线段中点为定点．
2．（2023·福建泉州·统考模拟预测）已知椭圆的离心率是，上、下顶点分别为，.圆与轴正半轴的交点为，且.
(1)求的方程；
(2)直线与圆相切且与相交于，两点，证明：以为直径的圆恒过定点.
3．（2023·四川南充·四川省南充高级中学校考三模）已知椭圆的左、右焦点为，离心率为.点是椭圆上不同于顶点的任意一点，射线分别与椭圆交于点，的周长为8.
(1)求椭圆的标准方程；
(2)设，，的面积分别为.求证：为定值.
4．（2023·江苏常州·校考一模）已知椭圆：的短轴长为，离心率为．
(1)求椭圆的方程；
(2)过点的动直线与椭圆相交于不同的两点，在线段上取点，满足，证明：点总在某定直线上．
5．（2023·河北秦皇岛·校联考二模）已知双曲线实轴的一个端点是，虚轴的一个端点是，直线与双曲线的一条渐近线的交点为.
(1)求双曲线的方程；
(2)若直线与曲线有两个不同的交点是坐标原点，求的面积最小值.