吉林省长春市农安县2025届九年级上学期10月期中考试数学试卷(含解析)

这是一份吉林省长春市农安县2025届九年级上学期10月期中考试数学试卷(含解析)，共16页。
注意事项：
1.本试卷共六页，包括三道大题，28道小题，全卷满分120分．
2.答题前，考生务必将自己的姓名、学校、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．
3.答题时，考生务必按照考试要求在答题卡的制定区域内作答，在草稿纸、试卷上答题无效．
一、选择题（每小题3分，共30分）
1．下列方程中，属于一元二次方程的是（ ）．
A．B．
C．D．
2．若，则（ ）
A．B．C．2D．5
3．方程的二次项系数、一次项系数、常数项分别为（ ）
A．4、、B．4、2、C．4、、1D．4、2、1
4．一元二次方程配方可变形为（ ）
A．B．C．D．
5．下列运算正确的是（ ）
A．B．
C．D．
6．下列四组线段中，是成比例线段的一组是（ ）
A．，，，B．，，，
C．，，，D．，，，
7．下列二次根式中属于最简二次根式的是（ ）
A．B．C．D．
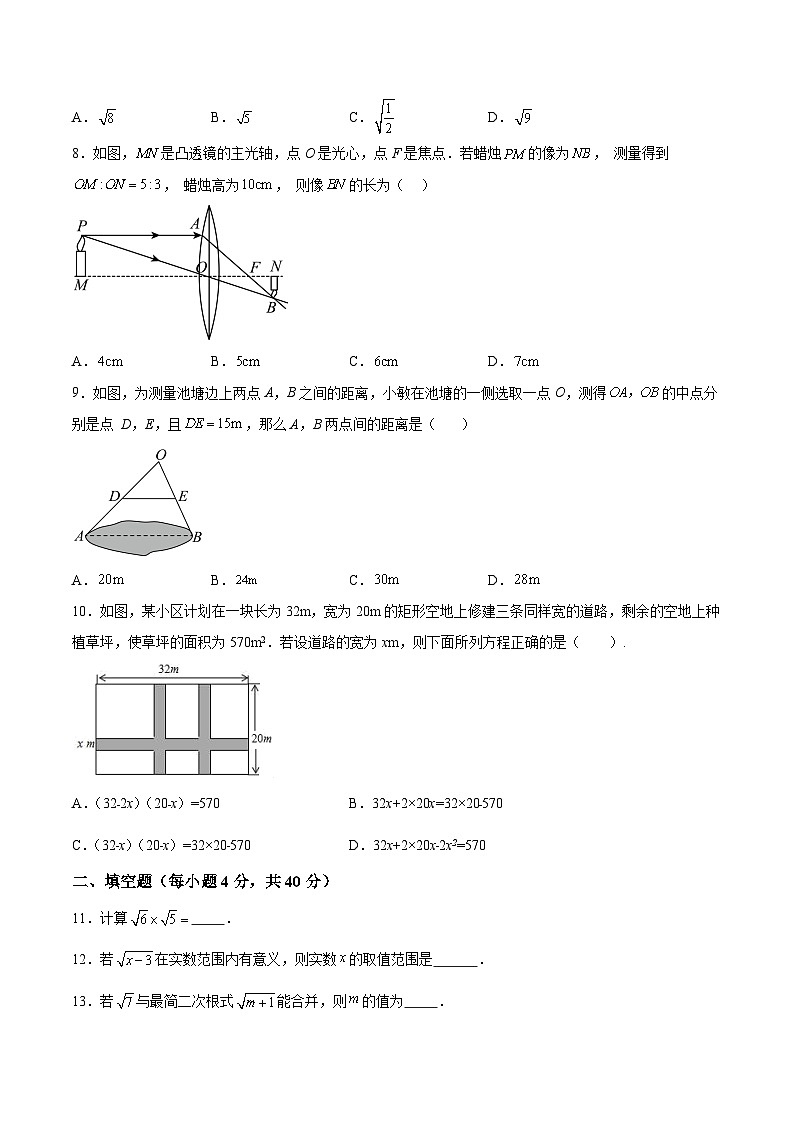
8．如图，是凸透镜的主光轴，点O是光心，点F是焦点．若蜡烛的像为， 测量得到， 蜡烛高为， 则像的长为（ ）
A．B．C．D．
9．如图，为测量池塘边上两点A，B之间的距离，小敏在池塘的一侧选取一点O，测得的中点分别是点 D，E，且，那么A，B两点间的距离是（ ）
A．B．C．D．
10．如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2．若设道路的宽为xm，则下面所列方程正确的是（ ）.
A．（32﹣2x）（20﹣x）=570B．32x+2×20x=32×20﹣570
C．（32﹣x）（20﹣x）=32×20﹣570D．32x+2×20x﹣2x2=570
二、填空题（每小题4分，共40分）
11．计算 ．
12．若在实数范围内有意义，则实数的取值范围是 ．
13．若与最简二次根式能合并，则的值为 ．
14．一元二次方程方程的根的判别式的值为 ．
15．已知，是方程的两个根，则x1+x2的值是 ．
16．地图上两地间的距离（图上距离）为3厘米，比例尺是1：1000000，那么两地间的实际距离是 米．
17．如图在中，是三角形的重心，，，则的长为 ．
18．如图，，若，，，则的长是 ．
19．如图，四边形中，，若，则 ．
20．按下列方法，将的三边缩小为原来的，如图所示，任取一点，连接，，，并取它们的中点D，E，F，连接DE，，得到，则下列说法正确的序号有 ．
①与是位似图形；②与是相似图形；③与的周长之比为；④与的面积之比为．
三、解答题（21－24题各5分，25、26题各7分，27、28题各8分，共50分）
21．计算：
(1)
(2)
22．解方程
(1)
(2)
23．一种药品原价每盒48元，经过两次降价后每盒27元，且两次降价的百分率相同，求每次降价的百分率．
24．求证：对于任意实数，关于的方程总有两个不相等的实数根．
25．如图，在平行四边形中，E为边上一点，连接，为线段上一点，且．求证：．
26．如图，在平面直角坐标系中，的顶点坐标分别为、O0,0、．

(1)画出将向左平移3个单位，再向上平移1个单位后的；
(2)以原点为位似中心，位似比为，在轴的左侧，画出将放大后的；
(3)判断与，能否是关于某一点为位似中心的位似图形，若是，请直接写出点的坐标．
27．阅读材料：黑白双雄，纵横江湖；双剑合璧，天下无敌．这是武侠小说中的常见描述，其意指两个人合在一起，取长补短，威力无比．在二次根式中也有这样相辅相成的例子．如：；，它们的积是有理数，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理化因式．于是，二次根式除法可以这样解：如；，像这样，通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去，叫作分母有理化．解决问题：
(1)的有理化因式是______，分母有理化得______；
(2)比较大小：______（用“”“”或“”填空）；
(3)计算：．
28．【感知】如图①，在正方形中，E为边上一点，连结，过点E作交于点F．易证：．（不需要证明）
【探究】如图②，在矩形中，E为边上一点，连结，过点E作交于点F．
（1）求证：；
（2）若，，E为的中点，求的长．
【应用】如图③，在中，，，．E为边上一点（点E不与点A、B重合），连结，过点E作交于点F．当为等腰三角形时，的长为__________．

1．B
解：A，，含有两个未知数，不是一元二次方程，不合题意；
B，是一元二次方程，符合题意；
C，，含有两个未知数，不是一元二次方程，不合题意；
D，不是整式方程，不是一元二次方程，不合题意；
故选B．
2．B
解：两边都除以，得
，
故选：B．
3．C
解：∵
∴
∴．
故选C．
4．A
解：，
∴，
∴，
故选：A．
5．A
解：A、，原式计算正确，符合题意；
B、，原式计算错误，不符合题意；
C、，原式计算错误，不符合题意；
D、，原式计算错误，不符合题意；
故选：A．
6．C
解：A、，不成比例，不符合题意；
B、，不成比例，不符合题意；
C、，成比例，符合题意；
D、，不成比例，不符合题意．
故选：C．
7．B
解：A、，故不是最简二次根式，不符合题意；
B、是最简二次根式，符合题意；
C、，故不是最简二次根式，不符合题意；
D、，故不是最简二次根式，不符合题意；
故选：B．
8．C
解：根据题意可得：，
∵，
∴，
∴，
∵，
∴，
故选：C．
9．C
解：∵ 的中点分别是点 D，E,
∴．
故选：C．
10．A
解：设道路的宽为xm，根据题意得：
(32−2x)(20−x)=570，
故选：A
【点睛】本题考查根据题意列方程.理解题意是解题的关键.
11．
解：，
故答案为：．
12．
解：由二次根式有意义的条件可得：，
解得：，
故答案为：．
13．
解：∵与最简二次根式能合并，
∴，
解得，
故答案为：．
14．
解：，
故答案为：．
15．
解：∵x1，x2是方程2x2-5x-1=0的两个根，
∴x1+x2=-.
故答案是：.
16．
解：设两地间的实际距离为厘米，
根据题意，
解得厘米米．
即实际距离是米．
故答案为：．
17．
解：延长交于点H，
则H是的中点，
∴，
又∵是三角形的重心，
∴，
故答案为：．
18．6
解：∵，
∴，即，
∴，
∴，
故答案为：6．
19．
解：∵，
∴，
∴，
∵，
∴，
∴，
∴，
故答案为：．
20．①②③
解：如图符合位似图形的定义，
∴①与是位似图形， 正确；
∵位似是相似的特殊形式，
∴②与是相似图形， 正确；
∴③与周长之比等于相似比为，正确；
∴④与的面积之比等于相似比的平方为， 错误；
∴正确的为：①②③．
故答案为：①②③．
21．(1)
(2)
（1）解：原式
；
（2）解：原式
．
22．(1)，
(2)，
（1）解：∵，
∴，
解得，
（2）解：∵，
∴，
∴，
∴，
∴，
解得，．
23．每次降价的百分率为
解：设每次降价的百分率为，
，
解得：，（舍去），
答：每次降价的百分率为．
24．见解析
解：
．
，
．
对于任意实数，关于的方程总有两个不相等的实数根．
25．见解析
解：证明：∵四边形是平行四边形，
∴，，
∴，，
∵，，
∴，
∴．
26．(1)见解析
(2)见解析
(3)是，Q点的坐标为
（1）解：根据题意，的顶点坐标分别为、O0,0、．
将向左平移3个单位，再向上平移1个单位后的坐标分别为、、．画图如下：

则即为所求．
（2）解：由、、．以原点为位似中心，位似比为，在轴的左侧，将放大后的坐标分别为、、．画图如下：

则即为所求．
（3）解：∵、O0,0、，、、．
∴直线为，
设直线的解析式为，
∴，
解得，
∴，
∴，
解得
故Q点的坐标为．
故与，是关于某一点为位似中心的位似图形，且位似中心为Q点的坐标为．
27．(1)；
(2)
(3)
（1）解：∵，
∴的有理化因式是，
∵，
∴分母有理化得，
故答案为：，；
（2）解：∵，，
又，
∴，
故答案为：．
（3）解：将分母有理化，可得
原式
．
28．[探究]（1）详见解析；（2）；[应用] 2或2
解：[探究]（1）证明：四边形是矩形，
，
．
，
，
，
，
又，
；
（2）为的中点，
，
由（1）知，
，即，
．
[应用]解：∵，，
∴，，
解得，，
∵，
∴，
∴；
由题意知，当为等腰三角形时，分，，，三种情况求解；
当时，则，
∴；
当时，，则，
∴，
∴，
∴；
当时，，
∴，此时不成立；
综上所述，的长为或2，
故答案为：或2．