初中数学华东师大版（2024）七年级下册（2024）第9章 轴对称、平移与旋转9.3 旋转3.旋转对称图形精品ppt课件

这是一份初中数学华东师大版（2024）七年级下册（2024）第9章 轴对称、平移与旋转9.3 旋转3.旋转对称图形精品ppt课件，共19页。PPT课件主要包含了旋转的特征有哪些，试一试，对角线的交点，旋转对称图形等内容，欢迎下载使用。
1. 通过具体实例认识旋转对称图形.2. 能按要求作出简单平面图形旋转后的图形.（重点）3. 会求一个旋转对称图形绕着旋转中心旋转多少度 (小于周角) 后，能与原图形重合.（难点）
(2)对应点到旋转中心的距离相等；
(4)图形的形状和大小不变；
(1)图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度；
(5)旋转中心是唯一不动的点.
(3)对应线段相等，对应角相等；
在日常生活中，我们经常可以看到，一些图形绕着某一定点旋转一定的角度后能与自身重合.如图所示，电扇的叶片旋转120°、螺旋桨旋转180°后，都能与自身重合.
你能再举出一些这样的实例吗？
那么这样的图形，我们该如何称呼它呢？
知识点1 旋转对称图形的识别
用一张半透明的薄纸，覆盖在如图所示的图形上，在薄纸上画这个图形，使它与如图所示的图形重合.然后用一枚图钉在圆心处穿过，将薄纸绕着图钉旋转，观察旋转多少度 (小于周角) 后，薄纸上的图形能与原图形再一次重合.
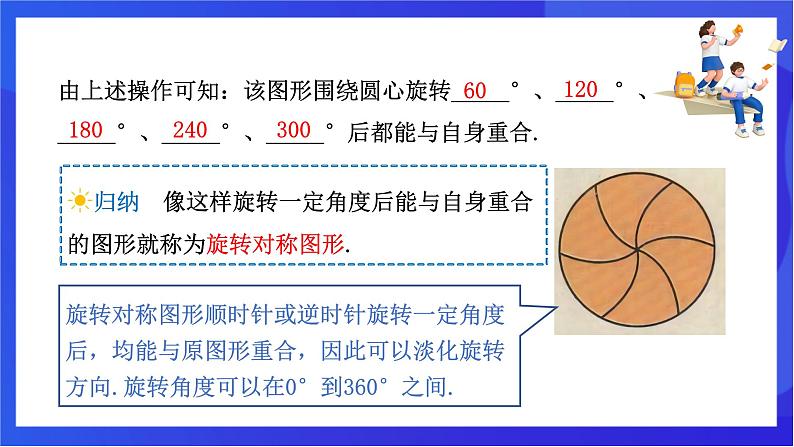
由上述操作可知：该图形围绕圆心旋转_____°、_____°、_____°、_____°、_____°后都能与自身重合.
☀归纳 像这样旋转一定角度后能与自身重合的图形就称为旋转对称图形.
旋转对称图形顺时针或逆时针旋转一定角度后，均能与原图形重合，因此可以淡化旋转方向.旋转角度可以在0°到360°之间.
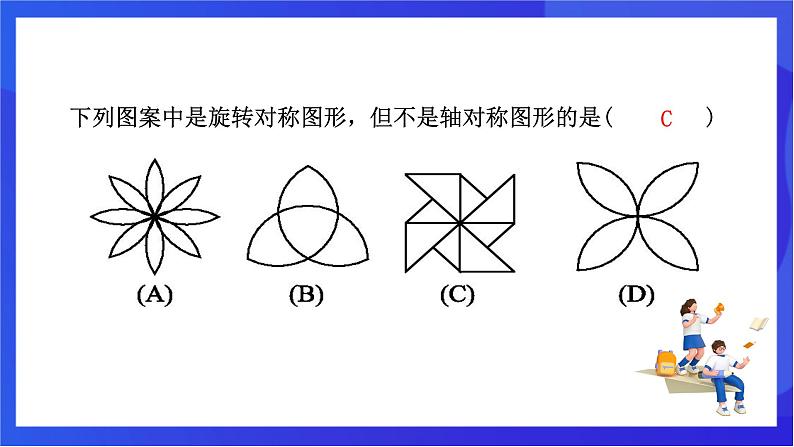
下列图案中是旋转对称图形，但不是轴对称图形的是(　 　)
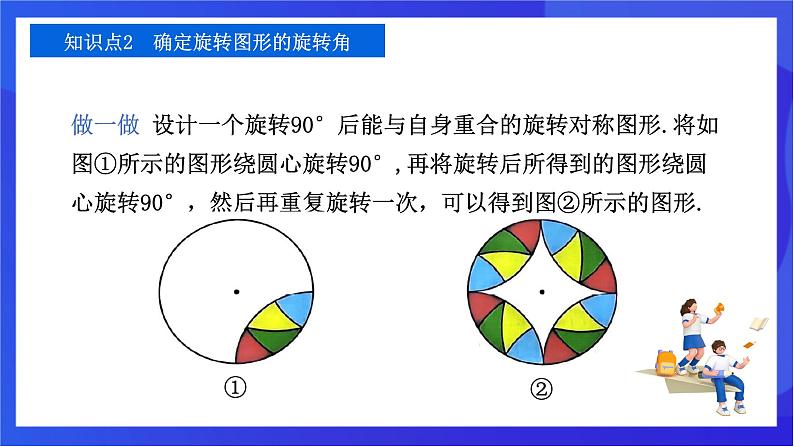
做一做 设计一个旋转90°后能与自身重合的旋转对称图形.将如图①所示的图形绕圆心旋转90°,再将旋转后所得到的图形绕圆心旋转90°，然后再重复旋转一次，可以得到图②所示的图形.
知识点2 确定旋转图形的旋转角
将如图所示的图形绕圆心旋转90°后，可以发现旋转以后的图形能与原来位置上的原图形重合，因此该图形是旋转对称图形.当然该图形绕圆心旋转180或270°后的图形也能与原图形重合，也可得出该图形是旋转对称图形.
☀归纳 旋转的度数称为旋转角度.
例1 下列各图形是不是旋转对称图形？如果是，请找出旋转中心在何处.旋转角度是多少？这些图形是轴对称图形吗？
答：这些图形都是旋转对称图形；旋转中心和其中一个旋转角度如图所示；这些图形都是轴对称图形.
☀归纳(1)绕着某一点转动一定角度后，能与自身重合的图形称为旋转对称图形.其中这一点就是旋转中心，这个角度就是旋转角度；(2)如果一个图形既是旋转对称图形，又是轴对称图形，那么它的旋转中心就是对称轴的交点；(3)正n边形既是旋转对称图形，又是轴对称图形，所以它的旋转中心就是对称轴的交点，并且其中一个旋转角度等于360°除于n所得的商.
下图可以看做是一个或几个菱形通过多次旋转得到的.
由一个菱形通过6次旋转得到，每次旋转60度.
由两个菱形旋转3次得到，每次旋转120度.
由三个菱形旋转2次得到，旋转180度.
1.如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n的最小值为( )A. 45B. 60 C. 72D. 144
2. 如图，在图 ①～④ 中是旋转对称图形的有( )A. 4 个B. 3 个 C. 2 个D. 1 个
3. 如图，其中不是旋转对称图形的是( )A. ①B. ② C. ③D. ④
4.下列多边形中，旋转60°后可以和原图形重合的是( )A. 正六边形B. 正五边形C. 正方形D. 正三角形5.等边△ABC绕着它的中心旋转，要使其与本身重合，至少旋转( )A. 60°B. 120°C. 180°D. 360°6.正方形绕它的________________旋转____度与自身重合；正六边形至少旋转____度，才能与自身重合.
旋转一定角度后能与自身重合的图形.
确定旋转对称图形的旋转角度