初中数学华东师大版（2024）七年级下册（2024）9.4 中心对称一等奖ppt课件

这是一份初中数学华东师大版（2024）七年级下册（2024）9.4 中心对称一等奖ppt课件，共22页。PPT课件主要包含了温馨提示，是中心对称图形，同一条直线，平行且等于CB，观察图形，OA′，OB′，OC′，A′O，B′O等内容，欢迎下载使用。
1. 理解中心对称图形与成中心对称的两个图形的概念，并且知道两者之间的区别与联系.（重点）2. 掌握它们的性质，会判断两个图形是否成中心对称，会画一个图形关于一个点成中心对称的图形.（难点）
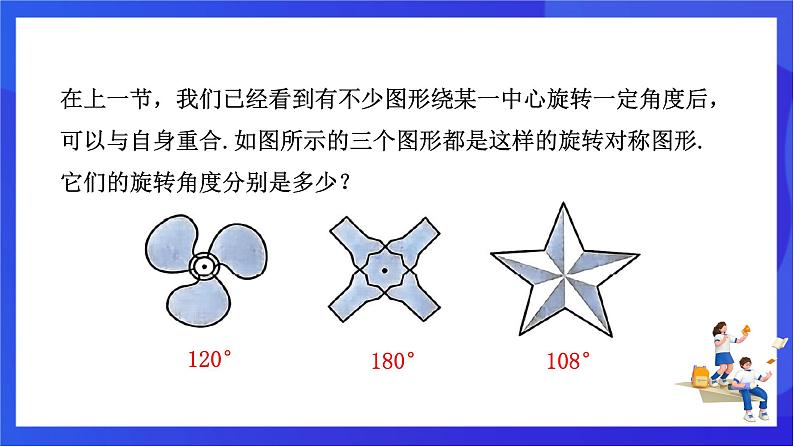
在上一节，我们已经看到有不少图形绕某一中心旋转一定角度后，可以与自身重合.如图所示的三个图形都是这样的旋转对称图形.它们的旋转角度分别是多少？
像中间的图形绕着中心旋转180°后能与自身重合，我们把这种图形叫做中心对称图形.这个中心叫做对称中心.所以，中心对称图形是旋转角度为180°的旋转对称图形.
你能举出日常生活中旋转 180°后能与自身重合的例子吗？
知识点1 中心对称图形
线段、三角形、平行四边形、正方形、圆分别是中心对称图形吗？如果是，那么对称中心又分别在哪里？
线段是中心对称图形，对称中心是线段的中点.
平行四边形是中心对称图形，对称中心是对角线的交点.
正方形是中心对称图形，对称中心是对角线的交点.
圆形是中心对称图形，对称中心是圆心.
☀(1) 中心对称图形的对称中心一定在图形内；(2) 中心对称图形是针对一个图形而言的；(3) 中心对称图形上所有的点关于对称中心的对称点都在这个图形本身上；(4) 中心对称图形一定是旋转对称图形，但旋转对称图形不一定是中心对称图形.
你能根据两个图形成轴对称的定义总结一下什么叫两个图形成中心对称吗？
把一个图形绕着某一点旋转180°，如果它能够和另一个图形重合，那么我们就说这两个图形成中心对称，这个点叫做对称中心，这两个图形中的对应点，叫做关于中心的对称点.
知识点2 两个图形成中心对称
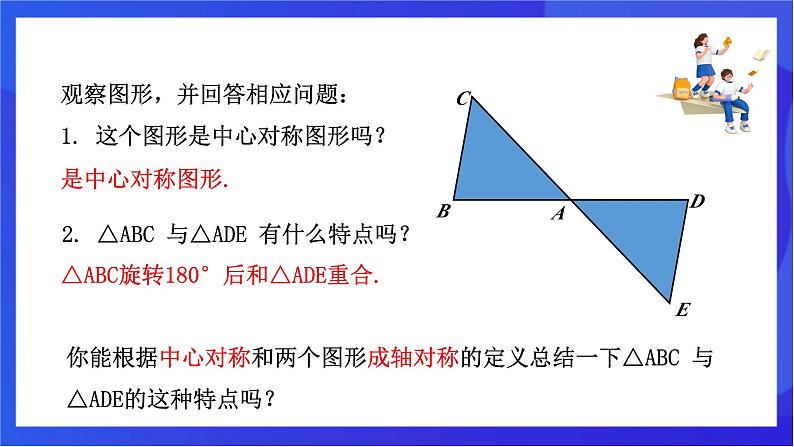
观察图形，并回答相应问题：1. 这个图形是中心对称图形吗？
2. △ABC 与△ADE 有什么特点吗？
△ABC旋转180°后和△ADE重合.
你能根据中心对称和两个图形成轴对称的定义总结一下△ABC 与△ADE的这种特点吗？
☀归纳 把一个图形绕着某一点旋转180°，如果它能够和另一个图形重合，那么我们就说这两个图形成中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点.
如图，△ABC与△ADE是成中心对称的两个三角形，点A是对称中心，点B关于对称中心A的对称点为_____，点C关于对称中心A的对称点是_____，点A关于对称中心A的对称点为_____，B、A、D 在___________上，AD=_____，C、A、E在___________上，AC =_____，ED______________.
可以发现，点A绕中心O旋转180°后到点A′,于是_________在同一直线上,并且AO=_____.另外分别在同一条直线上的三点还有________和________；并且BO=_____，CO=_____，AB=_____，AC=_____，BC=_____.
△ABC 与△A′B′C′关于点O成中心对称.你能从图中找到哪些等量关系？
知识点3 成中心对称的图形的特征
☀归纳 在成中心对称的两个图形中，连结对称点的线段都经过对称中心，并且被对称中心平分.反之，如果两个图形的对应点连成的线段都经过某一点，并且都被该点平分，那么这两个图形关于这一点成中心对称.
②成中心对称的两个图形的对称点分别在两个图形上，中心对称图形的对称点在一个图形上.
若把中心对称图形的两部分看成两个图形，则它们成中心对称；若把成中心对称的两个图形看成一个整体，那么这个整体也就是中心对称图形.
①成中心对称是指两个图形的关系，中心对称图形是指具有某种性质的图形.
例 如图，已知△ABC和点O，作△DEF，使△DEF和△ABC关于点O成中心对称.
知识点4 中心对称作图
解：(1) 连结AO并延长AO到点D，使OD = OA，于是得到点A关于点O的对称点D；(2)同样作出点B和点C关于点O的对称点E和F；(3)顺次连结DE、EF、FD.如图，△DFF即为所求的三角形.
如图，已知△ABC与△A′B′C′中心对称，找出它们的对称中心O.
解法1：根据观察，B、B′应是对应点，连接BB′，用尺规作图找出BB′的中点O，则点O即为所求（如图）.
解法2：根据观察，B、B′及C、C′应是两组对应点，连接BB′、CC′，BB′、CC′相交于点O，则点O即为所求（如图）.
注意：如果限制只用直尺作图，我们用解法2.
1.如下所示的4组图形中，左边数字与右边数字成中心对称的有 （ ） A.1组 B.2组 C.3组 D.4组
2.如图，已知△AOB与△DOC成中心对称，△AOB的面积是6，AB＝3，则△DOC中CD边上的高是（　　） A.2　　　 B.4　　　　　　 C.6　　 D.8
3.如图，已知四边形ABCD和点O，画四边形A′B′C′D′，使四边形 A′B′C′D′和四边形ABCD关于点O成中心对称.
如图，四边形A′B′C′D′即为所求.
旋转180°后与自身重合
1.对称中心与两对称点三点共线；2.成中心对称的两个图形是全等形.
应用1：作中心对称图形；应用2：找出对称中心.