初中数学北师大版（2024）七年级下册（2024）2 探索直线平行的条件同步测试题

这是一份初中数学北师大版（2024）七年级下册（2024）2 探索直线平行的条件同步测试题，共7页。试卷主要包含了2 等内容，欢迎下载使用。
一、选择题（每题5分，共25分）
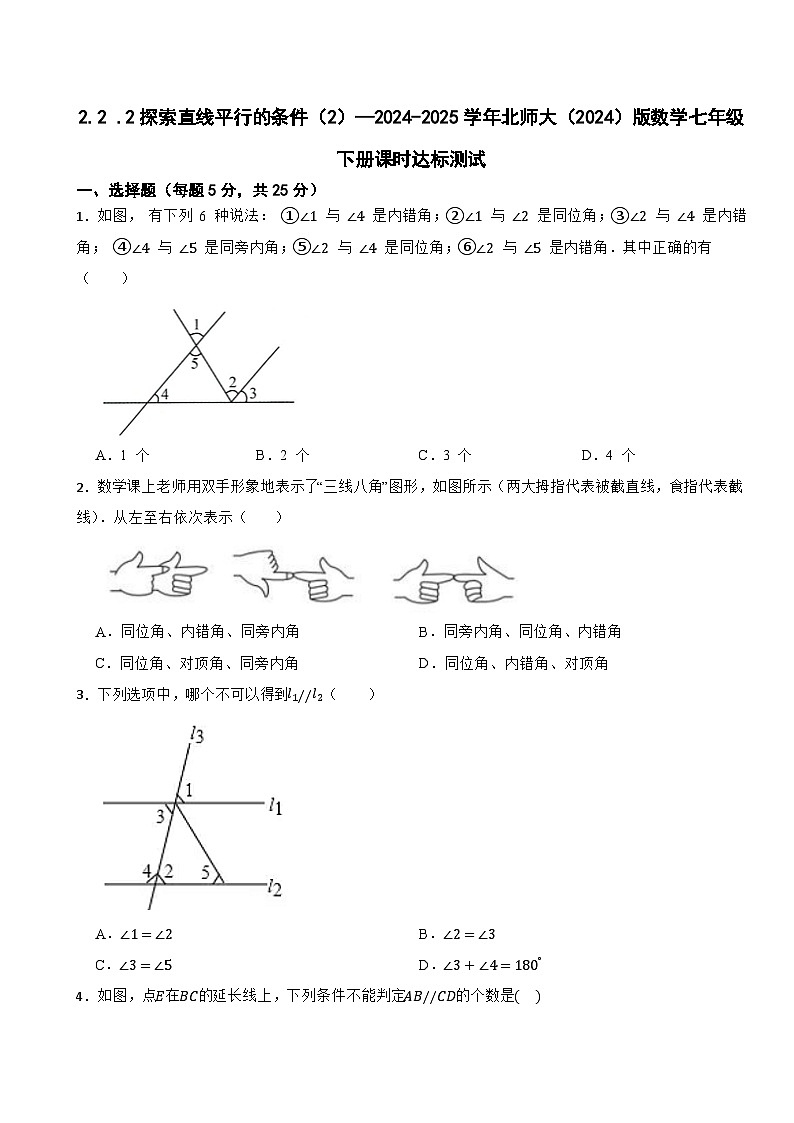
1．如图， 有下列 6 种说法： ①∠1 与 ∠4 是内错角；②∠1 与 ∠2 是同位角；③∠2 与 ∠4 是内错角； ④∠4 与 ∠5 是同旁内角；⑤∠2 与 ∠4 是同位角；⑥∠2 与 ∠5 是内错角．其中正确的有（ ）
A．1 个B．2 个C．3 个D．4 个
2．数学课上老师用双手形象地表示了“三线八角”图形，如图所示（两大拇指代表被截直线，食指代表截线）．从左至右依次表示（ ）
A．同位角、内错角、同旁内角B．同旁内角、同位角、内错角
C．同位角、对顶角、同旁内角D．同位角、内错角、对顶角
3．下列选项中，哪个不可以得到l1//l2（ ）
A．∠1=∠2B．∠2=∠3
C．∠3=∠5D．∠3+∠4=180°
4．如图，点E在BC的延长线上，下列条件不能判定AB//CD的个数是( )
①∠1=∠2 ②∠3=∠4
③∠DAB+∠B=180° ④∠D=∠5
A．1个B．2个C．3个D．4个
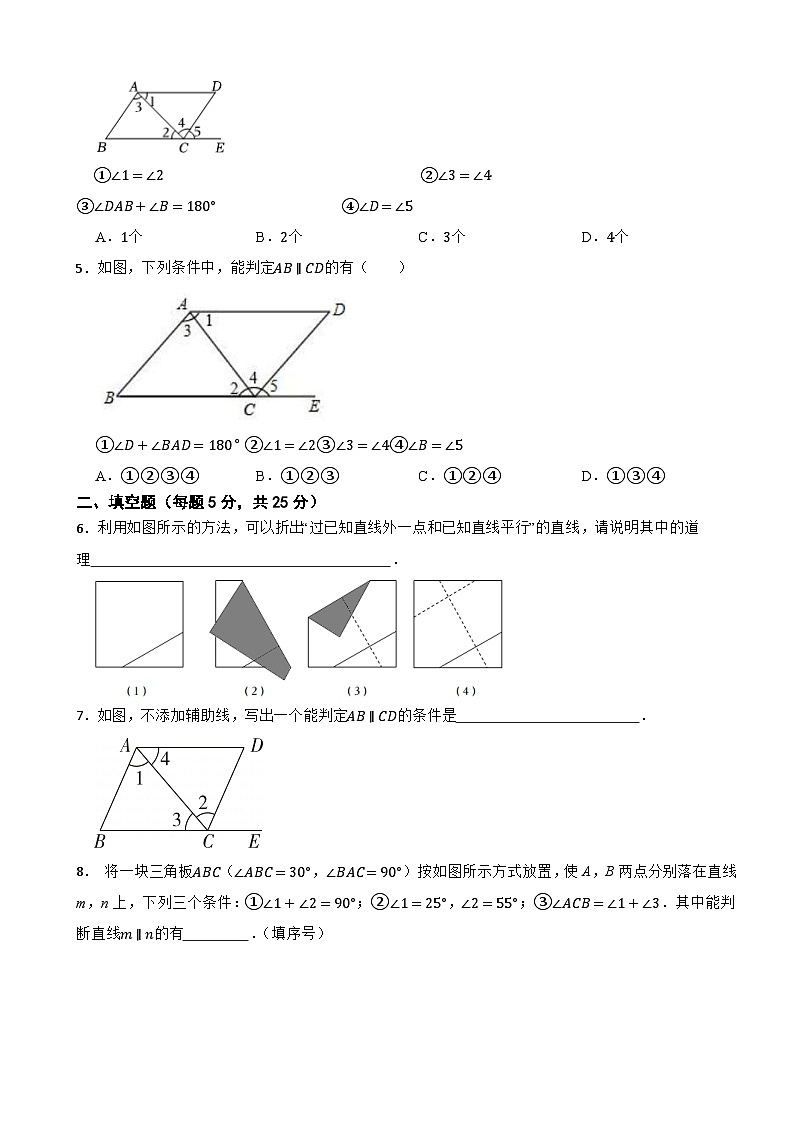
5．如图，下列条件中，能判定AB∥CD的有（ ）
①∠D+∠BAD=180∘ ②∠1=∠2③∠3=∠4④∠B=∠5
A．①②③④B．①②③C．①②④D．①③④
二、填空题（每题5分，共25分）
6．利用如图所示的方法，可以折出“过已知直线外一点和已知直线平行”的直线，请说明其中的道理 ．
7．如图，不添加辅助线，写出一个能判定AB∥CD的条件是 ．
8． 将一块三角板ABC（∠ABC=30°，∠BAC=90°）按如图所示方式放置，使A，B两点分别落在直线m，n上，下列三个条件：①∠1+∠2=90°；②∠1=25°，∠2=55°；③∠ACB=∠1+∠3．其中能判断直线m∥n的有 ．（填序号）
9．如图，给出下列结论：①∠1与∠2是同旁内角；②∠1与∠3是同位角；③∠1与∠4是内错角；④∠1与∠5是同位角；⑤∠2与∠4是对顶角．其中说法正确的是 ．（填序号）
10．如图， 点 E 在 CD 的延长线上， 在下列条件： ①∠C=∠5； ②∠C+∠BDC=180∘； ③∠1=∠2； ④∠3 =∠4． 其中能判定 AC∥BD 的是 (将所有正确的序号都填入)
三、解答题（共5题，共50分）
11．如图，根据图形填空(括号内填依据).
（1）已知∠ABD=∠BDC，则 ∥ （ ）
（2）已知∠CBE=∠A，则 ∥ （ ）
（3）已知∠A+∠ADC=180°，则 ( ∥ )
（4）由 ，可得DB∥CE(同位角相等，两直线平行).
（5）由 ，可得DB∥CE(内错角相等，两直线平行).
（6）由 ，可得DB∥CE(同旁内角互补，两直线平行).
12．如图，点O在直线AB上，F是DE上一点，连接OF，OC平分∠AOF，OD平分∠BOF交DE于点D.
（1）试说明OC⊥OD；
（2）若∠D与∠1互余，试说明ED∥AB.
13． 如图，直线CD、EF交于点O，OA,OB分别平分∠COE和∠DOE，已知∠1+∠2=90°．
（1）若∠2:∠3=2:5，求∠BOF的度数．
（2）试判断AB与CD的位置关系，并说明理由；
14． 将一副三角板中的两个直角顶点 C 叠放在一起 (如图)， 其中 ∠A=30∘，∠B=60∘， ∠D=∠E=45∘．
（1） 若 ∠BCD=150∘， 求 ∠ACE 的度数．
（2） 若按住三角板 ABC 不动， 绕顶点 C 转动三角板 DCE， 试探究 ∠BCD 等于多少度时， CD∥AB， 并简要说明理由．
15． 如图，直线EF与CD交于点O，OA平分∠COE交直线l于点A，OB平分∠DOE交直线l于点B，且∠1+∠2=90°．
（1）求∠AOB的度数：
（2）求证：AB∥CD；
（3）若∠2：∠3=2：5，求∠AOF的度数．
答案解析部分
1．【答案】B
2．【答案】A
3．【答案】C
4．【答案】C
5．【答案】D
6．【答案】内错角相等，两直线平行（答案不唯一）
7．【答案】∠1=∠2，答案不唯一
8．【答案】②③
9．【答案】①②⑤
10．【答案】①②③
11．【答案】（1）AB；CD；内错角相等，两直线平行
（2）AD；BC；同位角相等，两直线平行
（3）AB；CD；同旁内角互补，两直线平行
（4）∠DBA=∠E
（5）∠DBC=∠BCE
（6）∠DBE+∠E=180°(或∠BDC+∠DCE=180°)
12．【答案】（1）解：因为OC平分∠AOF，OD平分∠BOF
所以∠COF=12∠AOF，∠DOF=12∠BOF.
因为∠AOF+∠BOF=180°，
所以∠COD=∠COF+∠DOF=12(∠AOF+∠BOF)=90°，
所以OC⊥OD.
（2）解：由（1）知∠COD=90°，
所以∠1+∠DOB=90°
因为∠D与∠1互余，
所以∠D+∠1=90°，
所以∠D=∠DOB，
所以ED∥AB.
13．【答案】（1）解：∵OB平分∠DOE，
∴∠BOE=∠2，
∵∠2:∠3=2:5，
∴设∠2=2α，则：∠BOE=2α,∠3=5α，
∴∠BOF=∠2+∠3=7α，
∵∠BOE+∠BOF=2α+7α=9α=180°，
∴α=20°，
∴∠BOF=7α=140°；
（2）解：AB∥CD，理由如下：
∵OA,OB分别平分∠COE和∠DOE，
∴∠COE=2∠AOC,∠DOE=2∠2，
∵∠COE+∠DOE=2(∠AOC+∠2)=180°，
∴∠2+∠AOC=90°，
∵∠1+∠2=90°，
∴∠1=∠AOC，
∴AB∥CD．
14．【答案】（1）解：∵∠BCA=∠ECD=90∘，∠BCD=150∘，
∴∠DCA=∠BCD−∠BCA=150∘−90∘=60∘，
∴∠ACE=∠ECD−∠DCA=90∘−60∘=30∘．
（2）解：当 ∠BCD=120∘ 或 60∘ 时， CD∥AB．
如图 1 ， 根据同旁内角互补， 两直线平行，
当 ∠B+∠BCD=180∘ 时， CD∥AB，
此时 ∠BCD=180∘−∠B=180∘−60∘=120∘．
如图 2， 根据内错角相等， 两直线平行，
当 ∠B=∠BCD=60∘ 时， CD∥AB．
15．【答案】（1）解：∵OA，OB分别平分∠COE和∠DOE，
∴∠AOE=12∠COE,∠BOE=12∠DOE，
∴∠AOB=∠AOE+∠BOE=12∠COE+12∠DOE=12×180°=90°.
（2）解：由（1）知∠AOC+∠2=180°−∠AOB=180°−90°=90°，
∵∠1+∠2=90°，
∴∠AOC=∠1
∴AB∥CD．
（3）解：
∵∠2:∠3=2:5，∠2=12∠DOE，
∴∠DOE:∠3=4:5，
∵∠DOE+∠3=180°，
∴∠DOE=180°×49=80°,∠3=180°×59=100°，
∴∠COE=∠3=100°，
∵OA平分∠COE，
∴∠AOE=12∠COE=50°，
∴∠AOF=180°−∠AOE=130°
∴∠AOF的度数为130°．