2025年新高考数学精析考点考点15函数模型的应用(3种核心题型+基础保分练+综合提升练+拓展冲刺练)(原卷版+解析)

这是一份2025年新高考数学精析考点考点15函数模型的应用(3种核心题型+基础保分练+综合提升练+拓展冲刺练)(原卷版+解析)，文件包含2025年新高考数学精析考点考点15函数模型的应用3种核心题型+基础保分练+综合提升练+拓展冲刺练原卷版docx、2025年新高考数学精析考点考点15函数模型的应用3种核心题型+基础保分练+综合提升练+拓展冲刺练解析版docx等2份试卷配套教学资源，其中试卷共73页， 欢迎下载使用。
1.了解指数函数、对数函数与一次函数增长速度的差异.
2.理解“指数爆炸”“对数增长”“直线上升”等术语的含义
3.能选择合适的函数模型刻画现实问题的变化规律，了解函数模型在社会生活中的广泛应用
【知识点】
1．三种函数模型的性质
2．常见的函数模型
【核心题型】
题型一 用函数图象刻画变化过程
判断函数图象与实际问题变化过程相吻合的两种方法
(1)构建函数模型法：当根据题意易构建函数模型时，先建立函数模型，再结合模型选择函数图象．
(2)验证法：根据实际问题中两变量的变化快慢等特点，结合函数图象的变化趋势，验证是否吻合，从中排除不符合实际的情况，选择出符合实际情况的答案．
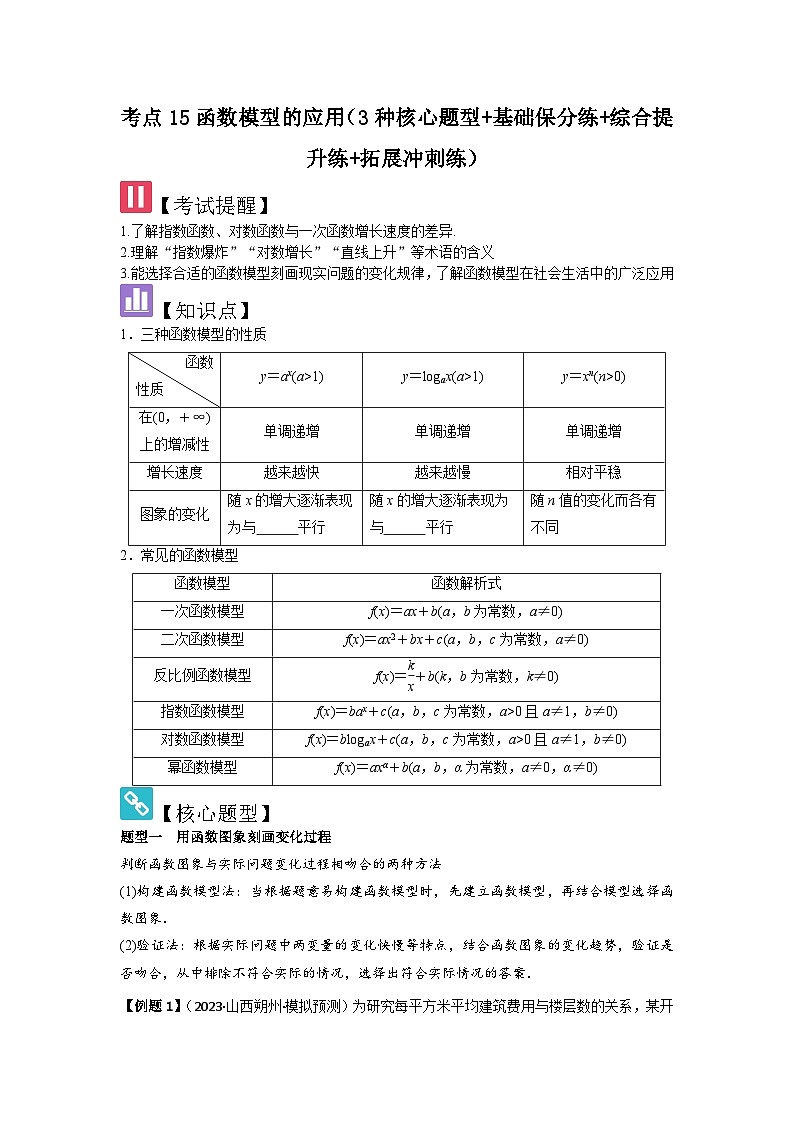
【例题1】（2023·山西朔州·模拟预测）为研究每平方米平均建筑费用与楼层数的关系，某开发商收集了一栋住宅楼在建筑过程中，建筑费用的相关信息，将总楼层数与每平米平均建筑成本（单位：万元）的数据整理成如图所示的散点图：
则下面四个回归方程类型中最适宜作为每平米平均建筑费用和楼层数的回归方程类型的是（ ）
A．B．
C．D．
【答案】C
【分析】通过观察散点图并结合选项函数的类型得出结果.
【详解】观察散点图，可知是一个单调递减的曲线图，结合选项函数的类型可得回归方程类型是反比例类型，故C正确.
故选：C
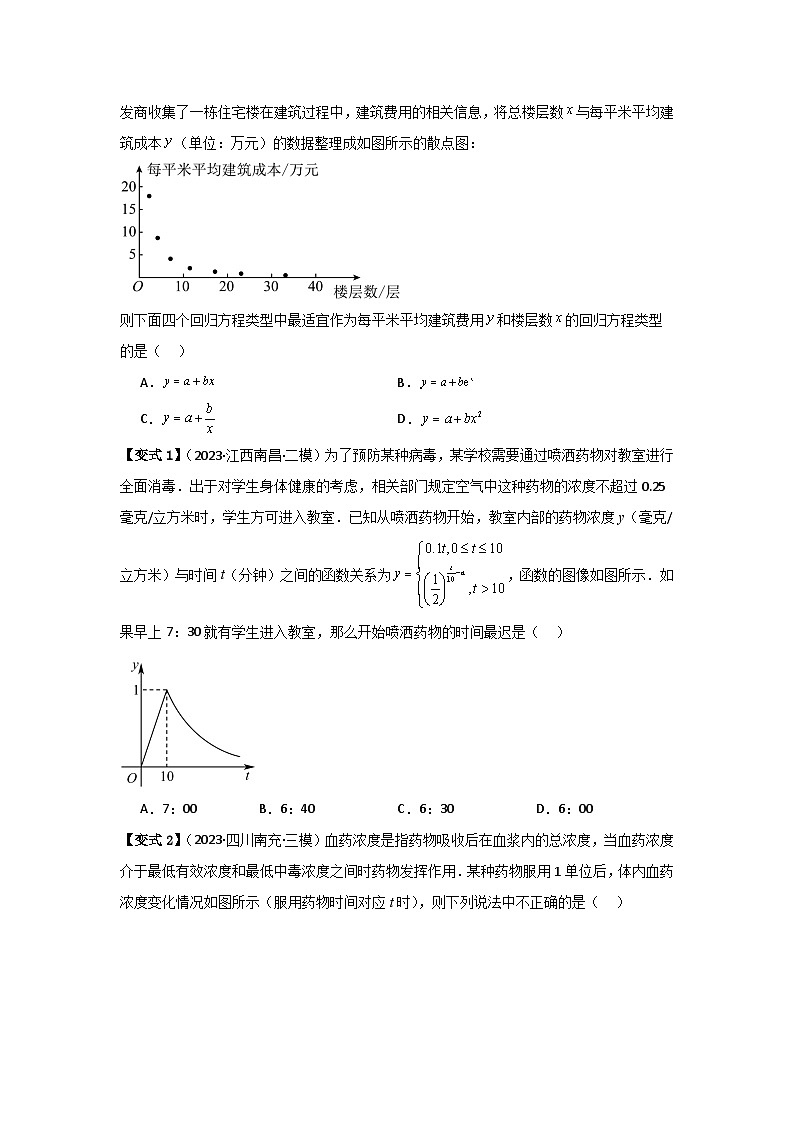
【变式1】（2023·江西南昌·二模）为了预防某种病毒，某学校需要通过喷洒药物对教室进行全面消毒．出于对学生身体健康的考虑，相关部门规定空气中这种药物的浓度不超过0.25毫克/立方米时，学生方可进入教室．已知从喷洒药物开始，教室内部的药物浓度y（毫克/立方米）与时间t（分钟）之间的函数关系为，函数的图像如图所示．如果早上7：30就有学生进入教室，那么开始喷洒药物的时间最迟是（ ）
A．7：00B．6：40C．6：30D．6：00
【答案】A
【分析】函数的图像过点，代入函数的解析式求得未知系数a，解函数不等式即可.
【详解】根据函数的图像，可得函数的图像过点，
由函数图像连续，代入函数的解析式，可得，解得，
所以，
令，可得或，
解得或．
所以如果7：30学生进入教室，那么开始喷洒药物的时间最迟是7：00．
故选：A
【变式2】（2023·四川南充·三模）血药浓度是指药物吸收后在血浆内的总浓度，当血药浓度介于最低有效浓度和最低中毒浓度之间时药物发挥作用．某种药物服用1单位后，体内血药浓度变化情况如图所示（服用药物时间对应t时），则下列说法中不正确的是（ ）
A．首次服药1单位后30分钟时，药物已经在发挥疗效
B．若每次服药1单位，首次服药1小时药物浓度达到峰值
C．若首次服药1单位，3小时后再次服药1单位，一定不会发生药物中毒
D．每间隔5.5小时服用该药物1单位，可使药物持续发挥治疗作用
【答案】C
【分析】根据所给图象及最低有效浓度、最低中毒浓度，逐项判断即可得解.
【详解】由图象知，当服药半小时后，血药浓度大于最低有效浓度，故药物已发挥疗效，故A正确；
由图象可知，首次服药1小时药物浓度达到峰值，故B正确；
首次服药1单位，3小时后再次服药1单位，经过1小时后，血药浓度超过，会发生药物中毒，故C错误；
服用该药物5.5小时后血药浓度达到最低有效浓度，再次服药可使血药浓度超过最低有效浓度且不超过最低中毒浓度，药物持续发挥治疗作用，故D正确.
故选：C
【变式3】（23-24高三下·江苏镇江·开学考试）函数的图象如图所示，则（ ）
A．B．
C．D．
【答案】D
【分析】由函数的定义域可判断的符号，分别令可判断的符号.
【详解】由，得，所以的定义域为，
由图可知，得，
令，则，得，
由图可知，得，
令，得，由图可知，得，
所以，
综上，，，，
故选：D
题型二 已知函数模型的实际问题
已知函数模型解决实际问题的关键
(1)认清所给函数模型，弄清哪些量为待定系数．
(2)根据已知利用待定系数法，确定模型中的待定系数．
(3)利用该函数模型，借助函数的性质、导数等求解实际问题，并进行检验．
【例题1】．（2024高三·全国·专题练习）中国茶文化博大精深，茶水的口感与茶叶类型和水的温度有关，经验表明，某种绿茶用的开水泡制，再等茶水温度降至时饮用，可以产生最佳口感，如果茶水原来的温度是，经过一定时间后的温度T(单位：)可由公式求得，其中表示室温，k是一个随着物体与空气的接触状况而定的正常数．现有一杯的绿茶放在室温为的房间中，如果茶温降到需要 ，那么在室温下，用的开水泡制，刚泡好的茶水要达到最佳饮用口感，大约需要放置（ ）(参考数据：)
A．B．C．D．
【答案】C
【分析】一杯的绿茶放在室温为的房间中，茶温降到需要 代入公式得；茶温降到需要代入公式得，结合题中数据可求得.
【详解】因为一杯的绿茶放在室温为的房间中，如果茶温降到需要 ，
则，整理得，解得，
一杯的绿茶放在室温为的房间中，如果茶温降到需要，
则，整理得，解得，
所以大约需要.
故选：C
【变式1】（2024·四川德阳·三模）如今我国物流行业蓬勃发展，极大地促进了社会经济发展和资源整合．已知某类果蔬的保鲜时间y(单位：小时)与储藏温度x(单位：℃)满足函数关系．(a，b．为常数)，若该果蔬在7℃的保鲜时间为288小时，在21℃ 的保鲜时间为32小时，且该果蔬所需物流时间为4天，则物流过程中果蔬的储藏温度(假设物流过程中恒温)最高不能超过（ ）
A．14℃B．15℃C．13℃D．16℃
【答案】A
【分析】根据给定的函数模型建立方程组，再列出不等式即可求解.
【详解】依题意，，则，即，显然，
设物流过程中果蔬的储藏温度为t℃，于是，
解得，因此，
所以物流过程中果蔬的储藏温度最高不能超过14℃.
故选：A
【变式2】（2023·贵州铜仁·模拟预测）牛顿曾经提出了在常温环境下的温度冷却模型（t为时间，单位：分钟，为环境温度，为物体初始温度，为冷却后温度），假设一杯开水温度，环境温度，常数，大约经过 分钟水温降为30℃（参考数据：）．
【答案】
【分析】代入数据，结合指数与对数性质运算即可得.
【详解】由题意，则，所以分钟．
故答案为：.
【变式3】（2024高三·全国·专题练习）环保部门为了研究某池塘里某种植物生长面积S(单位：)与时间t(单位：月)之间的关系，通过观察建立了函数模型，且.已知第一个月该植物的生长面积为，第三个月该植物的生长面积为.
(1)求证：若，则；
(2)若该植物的生长面积达到100 以上，则至少要经过多少个月？
【答案】(1)证明见解析
(2)8个月
【分析】（1）先根据条件求出参数，利用指数的运算可得答案；
（2）根据题意可得，求解指数不等式即可.
【详解】（1）证明：∵，∴.
∴.
由，得，∴.
（2）令，又，，
∴，即至少需要经过8个月
题型三 构造函数模型的实际问题
构建函数模型解决实际问题的步骤
(1)建模：抽象出实际问题的数学模型；
(2)推理、演算：对数学模型进行逻辑推理或数学运算，得到问题在数学意义上的解；
(3)评价、解释：对求得的数学结果进行深入讨论，作出评价、解释，然后返回到原来的实际问题中去，得到实际问题的解．
【例题1】（23-24高三上·江苏南通·期末）某中学开展劳动实习，学生制作一个矩形框架的工艺品．要求将一个边长分别为10cm和20cm的矩形零件的四个顶点分别焊接在矩形框架的四条边上，则矩形框架周长的最大值为（ ）
A．B．C．D．
【答案】D
【分析】由已知作图如图所示，设，利用三角函数表示各边长，借助三角函数性质计算可得结果.
【详解】如图所示，，
令，则，则，
，则
周长
，
故选：D．
【点睛】关键点睛：本题解决的关键是利用三角函数的定义表示出所求周长，再利用三角恒等变换即可得解
【变式1】（2023·陕西商洛·模拟预测）净水机通过分级过滤的方式使自来水逐步达到纯净水的标准，其工作原理中有多次的棉滤芯过滤，其中第一级过滤一般由孔径为5微米的棉滤芯（聚丙烯熔喷滤芯）构成，其结构是多层式，主要用于去除铁锈、泥沙、悬浮物等各种大颗粒杂质，假设每一层棉滤芯可以过滤掉三分之一的大颗粒杂质，若过滤前水中大颗粒杂质含量为80mg/L，现要满足过滤后水中大颗粒杂质含量不超过2mg/L，则棉滤芯的层数最少为（参考数据：，）（ ）
A．9B．8C．7D．6
【答案】A
【分析】首先由条件抽象出经过层棉滤芯过滤后的大颗粒杂质含量的函数，再结合指对运算，解不等式.
【详解】设经过层棉滤芯过滤后的大颗粒杂质含量为，则，
令，解得，两边取常用对数得，即
即，因为，，
所以，解得，因为，所以的最小值为9．
故选：A
【变式2】2023·上海闵行·三模）珠穆朗玛峰高达8848.86米，但即使你拥有良好的视力，你也无法在上海看到它．一个观察者距离珠穆朗玛峰多远，才能在底面上看到它呢？为了能够通过几何方法解决这个问题，需要利用简单的几何模型表示这个问题情境，在此过程中，有下列假设：①珠穆朗玛峰的形状为等腰梯形；②地球的形状是一个球体；③太阳光线沿直线传播；④没有事物可以阻碍人们看到珠穆朗玛峰的视线．你认为最不重要的一个假设是 ．
【答案】①
【分析】由数学建模时，假设针对问题的主要因素，忽略次要因素的原则，即可得出答案．
【详解】数学建模时，针对问题的主要因素，忽略次要因素，这里我们需要测量观察者距离珠穆朗玛峰多远，主要关注的应该是珠穆朗玛峰的高度，此时，珠穆朗玛峰的形状对于测量结果影响很小，故假设①最不重要，
故答案为：①．
【变式3】（23-24高三上·福建宁德·期中）为了减少碳排放，某企业采用新工艺，将生产中产生的二氧化碳转化为一种化工产品.已知该企业每月的处理量最少为30吨，最多为400吨.月处理成本（元）与月处理量（吨）之间的函数关系近似地表示为.
(1)该企业每月处理量为多少吨时，才能使月处理成本最低?月处理成本最低是多少元?
(2)该企业每月处理量为多少吨时，才能使每吨的平均处理成本最低?每吨的平均处理成本最低是多少元?
【答案】(1)企业每月处理量为300吨时，成本最低，最低为19800元
(2)企业每月处理量为360吨时，每吨的平均处理成本最低，最低60元
【分析】（1）由函数单调性得到最值；
（2）得到每吨的平均处理成本，利用基本不等式求出最值.
【详解】（1）该企业的月处理成本，
因为，在上单调递减，在上单调递增，
所以该企业每月处理量为300吨时，才能使月处理成本最低，月处理成本最低是19800元.
（2）因为，
所以每吨的平均处理成本.
因为，当且仅当时，等号成立，
所以，
即该企业每月处理量为360吨时，每吨的平均处理成本最低，为60元
【课后强化】
基础保分练
一、单选题
1．（2024·江苏·一模）德国天文学家约翰尼斯·开普勒根据丹麦天文学家第谷·布拉赫等人的观测资料和星表，通过本人的观测和分析后，于1618年在《宇宙和谐论》中提出了行星运动第三定律——绕以太阳为焦点的椭圆轨道运行的所有行星，其椭圆轨道的长半轴长a与公转周期T有如下关系：，其中M为太阳质量，G为引力常量．已知火星的公转周期约为水星的8倍，则火星的椭圆轨道的长半轴长约为水星的（ ）
A．2倍B．4倍C．6倍D．8倍
【答案】B
【分析】根据已知的公式，由周期的倍数关系求出长半轴长的倍数关系即可.
【详解】设火星的公转周期为，长半轴长为，火星的公转周期为，长半轴长为，
则，，且
得： ，
所以，，即：.
故选：B．
2．（2024·广东韶关·二模）在工程中估算平整一块矩形场地的工程量W（单位：平方米）的计算公式是，在不测量长和宽的情况下，若只知道这块矩形场地的面积是10000平方米，每平方米收费1元，请估算平整完这块场地所需的最少费用（单位：元）是（ ）
A．10000B．10480C．10816D．10818
【答案】C
【分析】设矩形场地的长为米，则，结合基本不等式计算即可求解.
【详解】设矩形场地的长为米，则宽为米，
，
当且仅当，即时，等号成立.
所以平整这块场地所需的最少费用为元.
故选：C
3．（2024·上海奉贤·二模）已知函数，其中，，其中，则图象如图所示的函数可能是（ ）．
A．B．
C．D．
【答案】A
【分析】根据函数图象和的奇偶性判断.
【详解】易知是偶函数， 是奇函数，给出的函数图象对应的是奇函数，
A. ，定义域为R，
又，所以是奇函数，符合题意，故正确；
B. ，，不符合图象，故错误；
C. ，定义域为R，
但，故函数是非奇非偶函数，故错误；
D. ，定义域为R，
但，故函数是非奇非偶函数，故错误，
故选：A
4．（2024·河南新乡·二模）某工厂产生的废气经过滤后排放，过滤过程中废气的污染物含量P（单位：）与时间t（单位：h）之间的关系式为，其中是正的常数，若在前消除了的污染物，则常数k所在的区间为（ ）
A．B．C．D．
【答案】B
【分析】首先由题意列式，再利用指对互化，求解方程，再确定范围.
【详解】由条件可知，当时，，由题意可知，，
得，即，
因为，，所以，
所以.
故选：B
5．（2024·内蒙古赤峰·一模）在下列四个图形中，点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O、P两点连线的距离y与点P走过的路程x的函数关系如图，那么点P所走的图形是（ ）
A．B．
C．D．
【答案】D
【分析】由点在第二条边上运动时，的单调性可排除A，由图象的对称性可排除，由一开始与是线性的可排除C，对于D，当图形是正方形时，可以验证它满足题意.
【详解】对于A，点在第一条边上时，，
但点在第二条边上运动时，是随的增大先减小（减到最小时即为三角形的第二条边上的高的长度），然后再增大，
对比图象可知，A错误；
对于B，y与x的函数图形一定不是对称的，B错误；
对于C，一开始与的关系不是线性的，C错误；
对于D，因为函数图象对称，所以D选项应为正方形，不妨设边长为，
点在第一条边上时（即时），，
点在第二条边上运动时（即时），，依然单调递增，
点在第三条边上运动时（即时），，单调递减，
点在第四条边上运动时（即时），，单调递减，
且已知与的图象关于（其中）对称，D正确.
故选：D.
二、多选题
6．（2024·全国·模拟预测）某地下车库在排气扇发生故障的情况下测得空气中一氧化碳含量达到了危险状态，经抢修排气扇恢复正常，排气4分钟后测得车库内的一氧化碳浓度为，继续排气4分钟后又测得浓度为．由检验知该地下车库一氧化碳浓度（单位：）与排气时间（单位：分钟）之间满足函数关系（为常数，是自然对数的底数）．若空气中一氧化碳浓度不高于，人就可以安全进入车库了，则下列说法正确的是（ ）
A．
B．
C．排气12分钟后浓度为
D．排气32分钟后，人可以安全进入车库
【答案】ACD
【分析】由题意列式，求出，即可判断A，B；可得函数解析式，将代入，即可判断C；结合解析式列出不等关系，求出人可以安全进入车库的排气时间，判断D.
【详解】设，代入，得,
解得，A正确，B错误．
此时，所以，C正确．
当时，即，得，所以，
所以排气32分钟后，人可以安全进入车库，D正确．
故选:ACD．
7．（2023·广东广州·三模）已知函数的图象与直线有三个交点，记三个交点的横坐标分别为，且，则下列说法正确的是（ ）
A．存在实数，使得
B．
C．
D．为定值
【答案】BCD
【分析】化简方程，令，得，构造，则，利用函数的单调性，结合函数的图象，要使关于x的方程三个不相等的实数解，且，结合图象可得关于的方程一定有两个实根， ，结合韦达定理，推出所求表达式的关系式，然后对选项一一判断即可得出答案．
【详解】由方程，可得．
令，则有，即．
令函数，则，
令，解得，令，解得，
所以在上单调递增，在上单调递减，
所以，作出图象如图所示，
要使关于的方程有三个不相等的实数解，且，
结合图象可得关于的方程一定有两个实根，，
且，或，，
令，若，，
则故．
若，，则，无解，
综上：，故C正确；
由图结合单调性可知，故B正确；
若，则，又，故A不正确；，
故D正确，
故选：BCD．
【点睛】关键点点睛：构造，判断出函数的单调性，结合图象将，转化成关于t的函数即可求解.
三、填空题
8．（22-23高三下·上海闵行·阶段练习）一般的数学建模包含如下活动过程：①建立模型；②实际情境；③提出问题；④求解模型；⑤实际结果；⑥检验结果，请写出正确的序号顺序 ．
【答案】②③①④⑥⑤
【分析】根据给定条件，利用数学建模的活动过程及顺序写出结论作答.
【详解】数学建模活动，根据实际情境，提出问题，基于问题，建立模型，通过模型的求解，以检验模型解决问题的结果，
若结果不符合实际，还需重新建立模型；若结果符合实际，问题的回答便有了实际的结果，
所以正确的序号顺序是②③①④⑥⑤.
故答案为：②③①④⑥⑤
9．（2024·上海长宁·二模）甲、乙、丙三辆出租车2023年运营的相关数据如下表：
出租车空驶率；依据以述数据，小明建立了求解三辆车的空驶率的模型，并求得甲、乙、丙的空驶率分别为，则 （精确到0.01）
【答案】
【分析】根据题意得到出租车空驶率的模型，检验甲、乙两辆出租车的空驶率，满足题意，从而利用该模型求得丙的空驶率，从而得解.
【详解】依题意，因为出租车行驶的总里程为，出租车有载客时行驶的里程为，
所以出租车空驶率，
对于甲，，满足题意；
对于乙，，满足题意；
所以上述模型满足要求，
则丙的空驶率为，即.
故答案为：.
四、解答题
10．（2024·浙江温州·二模）红旗淀粉厂2024年之前只生产食品淀粉，下表为年投入资金（万元）与年收益（万元）的8组数据：
(1)用模拟生产食品淀粉年收益与年投入资金的关系，求出回归方程；
(2)为响应国家“加快调整产业结构”的号召，该企业又自主研发出一种药用淀粉，预计其收益为投入的．2024年该企业计划投入200万元用于生产两种淀粉，求年收益的最大值．（精确到0.1万元）
附：①回归直线中斜率和截距的最小二乘估计公式分别为：，
②
③
【答案】(1)
(2)36.5
【分析】（1）利用回归直线的公式求和的值，可得回归方程.
（2）建立函数关系，利用导数分析函数单调性，求出函数的最大值.
【详解】（1）
∴回归方程为：
（2）2024年设该企业投入食品淀粉生产x万元，预计收益（万元）
，
，得
∴其在上递增，上递减
11．（2024·江西上饶·一模）机动车辆保险即汽车保险（简称车险），是指对机动车辆由于自然灾害或意外事故所造成的人身伤亡或财产损失负赔偿责任的一种商业保险．机动车辆保险一般包括交强险和商业险两部分，其中商业险包括基本险和附加险．经验表明商业险保费（单位：元）由过去三年的出险次数决定了下一年的保费倍率，上饶市某机动车辆保险公司对于购买保险满三年的汽车按如下表格计算商业险费用．（假设每年出险次数2次及以上按2次计算）
(1)汽车的基准保费由车的价格决定，假定王先生的汽车基准保费为3000元，且过去8年都没有出险，近期发生轻微事故，王先生到汽车维修店询价得知维修费为1000元，理赔人员根据王先生过去一直安全行车的习惯，建议王先生出险理赔，王先生是否该接受建议？（假设接下来三年王先生汽车基准保费不变，且都不出险）
(2)张先生有多年驾车经验，用他过去的驾车出险频率估计概率，得知平均每年不出险的概率为0.8，出一次险的概率为0.1，出两次险的概率为0.1（两次及以上按两次算）．张先生近期买了一辆新车，商业险基准保费为3000元（假设基准保费不变），求张先生新车刚满三年时的商业险保费分布列及期望．
【答案】(1)接受建议
(2)分布列见解析；期望为（元）
【分析】（1）计算出险和不出险两种情况的缴费情况，将差值与1000计较即可得结论；
（2）列出的可能值，分别计算概率再计算期望即可.
【详解】（1）由于王先生过去三年都没有出险，
若不出险，王先生接下来三年只需按最低标准1800元缴费，共需5400元．
若进行理赔，则接下来三年每年需2100元，共需6300元
，故出险理赔更划算.
（2）设商业险保费数额为随机变量，
则的可能值为5400，4500，3600，3000，2400，2100，1800．
则
则
（元）
综合提升练
一、单选题
1．（2023·河南郑州·模拟预测）水雾喷头布置的基本原则是：保护对象的水雾喷头数量应根据设计喷雾强度、保护面积和水雾喷头特性，按水雾喷头流量q（单位：L/min）计算公式为和保护对象的水雾喷头数量N计算公式为计算确定，其中P为水雾喷头的工作压力（单位：MPa），K为水雾喷头的流量系数（其值由喷头制造商提供），S为保护对象的保护面积，W为保护对象的设计喷雾强度（单位：）．水雾喷头的布置应使水雾直接喷射和完全覆盖保护对象，如不能满足要求时应增加水雾喷头的数量．当水雾喷头的工作压力P为0.35MPa，水雾喷头的流量系数K为24.96，保护对象的保护面积S为，保护对象的设计喷雾强度W为时，保护对象的水雾喷头的数量N约为（参考数据：）（ ）
A．4个B．5个C．6个D．7个
【答案】C
【分析】把给定的数据代入公式计算即可作答.
【详解】依题意，，，，，
由，，得，
所以保护对象的水雾喷头的数量N约为6个.
故选：C
2．（23-24高三上·河南·阶段练习）设某批产品的产量为（单位：万件），总成本（单位：万元），销售单价（单位：元/件）．若该批产品全部售出，则总利润（总利润销售收入-总成本）最大时的产量为（ ）
A．7万件B．8万件C．9万件D．10万件
【答案】B
【分析】表达出总利润关于的关系式，变形后利用基本不等式求出最值，得到答案.
【详解】总利润
，当且仅当，
即时，最大，故总利润最大时的产量为8万件．
故选：B．
3．（2024·北京丰台·一模）按国际标准，复印纸幅面规格分为系列和系列，其中系列以，，…等来标记纸张的幅面规格，具体规格标准为：
①规格纸张的幅宽和幅长的比例关系为；
②将（）纸张平行幅宽方向裁开成两等份，便成为规格纸张（如图）．

某班级进行社会实践活动汇报，要用规格纸张裁剪其他规格纸张．共需规格纸张40张，规格纸张10张，规格纸张5张．为满足上述要求，至少提供规格纸张的张数为（ ）
A．6B．7C．8D．9
【答案】C
【分析】设一张规格纸张的面积为，从而得到一张、、纸的面积，再求出所需要的纸的总面积，即可判断.
【详解】依题意张规格纸张可以裁剪出张，或张或张，
设一张规格纸张的面积为，
则一张规格纸张的面积为，
一张规格纸张的面积为，
一张规格纸张的面积为，
依题意总共需要的纸张的面积为，
所以至少需要提供张规格纸张，
其中将张裁出张和张；将张裁出张；
将剩下的张裁出张，
即共可以裁出张、张、张.
故选：C
4．（2024·河北沧州·模拟预测）某企业的废水治理小组积极探索改良工艺，致力于使排放的废水中含有的污染物数量逐渐减少．已知改良工艺前排放的废水中含有的污染物数量为，首次改良工艺后排放的废水中含有的污染物数量为，第n次改良工艺后排放的废水中含有的污染物数量满足函数模型（，），其中为改良工艺前排放的废水中含有的污染物数量，为首次改良工艺后排放的废水中含有的污染物数量，n为改良工艺的次数．假设废水中含有的污染物数量不超过时符合废水排放标准，若该企业排放的废水符合排放标准，则改良工艺的次数最少为（ ）（参考数据：，）
A．12B．13C．14D．15
【答案】D
【分析】由题意，根据指数幂和对数运算的性质可得，由，解不等式即可求解.
【详解】由题意知，，
当时，，故，解得，
所以．
由，得，即，
得，又，
所以，
故若该企业排放的废水符合排放标准，则改良工艺的次数最少要15次．
故选：D
5．（2024·北京怀柔·模拟预测）“绿水青山就是金山银山”的理念已经提出18年，我国城乡深化河道生态环境治理，科学治污.现有某乡村一条污染河道的蓄水量为v立方米，每天的进出水量为k立方米，已知污染源以每天r个单位污染河水，某一时段t（单位：天）河水污染质量指数（每立方米河水所含的污染物）满足（为初始质量指数），经测算，河道蓄水量是每天进出水量的50倍.若从现在开始停止污染源，要使河水的污染水平下降到初始时的，需要的时间大约是（参考数据：，）（ ）
A．1个月B．3个月C．半年D．1年
【答案】B
【分析】由题意可知，，利用指数与对数的运算性质进行化简求解，即可得到答案．
【详解】由题意可知，，故，
则，即，
所以，则要使河水的污染水平下降到初始时的，需要的时间大约是90天，即三个月．
故选：B．
6．（2024·北京西城·一模）德国心理学家艾·宾浩斯研究发现，人类大脑对事物的遗忘是有规律的，他依据实验数据绘制出“遗忘曲线”．“遗忘曲线”中记忆率随时间（小时）变化的趋势可由函数近似描述，则记忆率为时经过的时间约为（ ）（参考数据：）
A．2小时B．0.8小时C．0.5小时D．0.2小时
【答案】C
【分析】根据题设得到，两边取对数求解，即可得出结果.
【详解】根据题意得，整理得到，两边取以为底的对数，
得到，即，又，
所以，得到，
故选：C.
7．（2023·湖北武汉·模拟预测）一个半球体状的雪堆，假设在融化过程中雪堆始终保持半球体状，其体积变化的速率与半球面面积成正比，已知半径为的雪堆在开始融化的3小时，融化了其体积的，则该雪堆全部融化需要（ ）小时
A．B．4C．5D．6
【答案】D
【分析】设雪堆在时刻的体积为，侧面积，依题意令，即可求出，令（为常数），求出，再根据求出，即可得解．
【详解】设雪堆在时刻的体积为，侧面积．
令，即于是，
令（为常数），由，得，故．
又，即，得，从而，
因雪堆全部融化时，，故，即雪堆全部融化需小时．
故选：D．
8．（2024·陕西商洛·三模）近年来商洛为了打造康养之都，引进了先进的污水、雨水过滤系统．已知过滤过程中废水的污染物数量与时间（小时）的关系为（为最初的污染物数量）．如果前3小时消除了的污染物，那么污染物消除至最初的还需要（ ）
A．2.6小时B．6小时C．3小时D．4小时
【答案】C
【分析】由题意可得，再令，即可得解.
【详解】由题意可得，可得，
设，
，解得，
因此，污染物消除至最初的还需要3小时．
故选：C.
二、多选题
9．（2024·重庆·模拟预测）放射性物质在衰变中产生辐射污染逐步引起了人们的关注，已知放射性物质数量随时间的衰变公式，表示物质的初始数量，是一个具有时间量纲的数，研究放射性物质常用到半衰期，半衰期指的是放射性物质数量从初始数量到衰变成一半所需的时间，已知，右表给出了铀的三种同位素τ的取值：若铀234、铀235和铀238的半衰期分别为，，，则（ ）
A．B．与成正比例关系
C．D．
【答案】BD
【分析】A选项，根据半衰期的定义得到，从而得到方程，求出；B选项，由A选项得到结论；C选项，由B选项可得C错误；D选项，计算出，作商得到D正确.
【详解】A选项，由题意得，
又，故，两边取对数得，，
，A错误；
B选项，由A可知，与成正比例关系，B正确；
C选项，由B可知，与成正比例关系，由于铀234的值小于铀235的值，
故，C错误；
D选项，，
，
故，D正确.
故选：BD
10．（2024·安徽蚌埠·模拟预测）科学研究表明，物体在空气中冷却的温度变化是有规律的．如果物体的初始温度为，空气温度保持不变，则t分钟后物体的温度（单位：）满足：．若空气温度为，该物体温度从（）下降到，大约所需的时间为，若该物体温度从，下降到，大约所需的时间分别为，则（ ）（参考数据：）
A．B．C．D．
【答案】BC
【分析】当时，可求得，继而求得，逐项判定即可.
【详解】有题意可知，，
当，则，
即，，
则，
其是关于的单调递增函数，
当时，，
当时，，
则，故B正确；
当时，，
故A错误；
当时，，
此时满足， ，故C正确，D错误，
故选：BC.
11．（2023·全国·模拟预测）第31届世界大学生夏季运动会在四川成都举行，大运会吉祥物“蓉宝”备受人们欢迎．某大型超市举行抽奖活动，推出“单次消费满1000元可参加抽奖”的活动，奖品为若干个大运会吉祥物“蓉宝”．抽奖结果分为五个等级，等级与获得“蓉宝”的个数的关系式为，已知三等奖比四等奖获得的“蓉宝”多2个，比五等奖获得的“蓉宝”多3个，且三等奖获得的“蓉宝”数是五等奖的2倍，则（ ）
A．B．
C．D．二等奖获得的“蓉宝”数为10
【答案】ABD
【分析】依题意，得出关于的方程组，解方程组得的值，从而得到关于的方程组，解方程组得的值，即可判断选项A，B，C是否正确，由的值推出的解析式，求出的值，即可判断选项D是否正确．
【详解】依题意，得，解得即：
对于选项A，由可得： ，（依题意知，，故）
得，所以，故A项正确；
对于选项B，因可得：，由选项A结论可知，
所以，所以，解得，故B项正确；
对于选项C，因可得：，由选项B结论，有，
解得，故C项错误；
对于选项D，由选项A，B，C可得，即，所以，
即二等奖获得的“蓉宝”数为10，故D项正确．
故选：ABD.
三、填空题
12．（2023·海南·模拟预测）新能源汽车是未来汽车的发展方向之一，一个新能源汽车制造厂引进了一条新能源汽车整车装配流水线，这条流水线生产的新能源汽车数量（辆）与创造的价值（万元）之间满足一次函数关系.已知产量为时，创造的价值也为；当产量为辆时，创造的价值达到最大，为万元.若这家工厂希望利用这条流水线创收达到万元，则它应该生产的新能源汽车数量是 .
【答案】
【分析】设，根据已知条件可求得，代入即可求得结果.
【详解】由题意可设：，则，解得：，，
则当时，，即应生产的新能源汽车辆.
故答案为：.
13．（2024·全国·模拟预测）药物的半衰期指的是血液中药物浓度降低到一半所需时间．在特定剂量范围内，（单位，h）内药物在血液中浓度由（单位，）降低到（单位，），则药物的半衰期．已知某时刻测得药物甲、乙在血液中浓度分别为和，经过一段时间后再次测得两种药物在血液中浓度都为，设药物甲、乙的半衰期分别为，，则 ．
【答案】2
【分析】根据题意代入即可求解.
【详解】由题意得，．
故答案为：2
14．（2023·上海崇明·二模）在一个十字路口，每次亮绿灯的时长为30秒，那么，每次绿灯亮时，在一条直行道路上能有多少汽车通过？这个问题涉及车长、车距、车速、堵塞的干扰等多种因素，不同型号车的车长是不同的，驾驶员的习惯不同也会使车距、车速不同，行人和非机动车的干扰因素则复杂且不确定．面对这些不同和不确定，需要作出假设．例如小明发现虽然通过路口的车辆各种各样，但多数是小轿车，因此小明给出如下假设：通过路口的车辆长度都相等，请写出一个你认为合理的假设 ．
【答案】①等待时，前后相邻两辆车的车距都相等（或②绿灯亮后，汽车都是在静止状态下匀加速启动；或③前一辆车启动后，下一辆车启动的延时时间相等；或④车辆行驶秩序良好，不会发生堵塞，等等）；（答案不唯一，只要写出一个即可）
【分析】利用数学建模，根据题意这次建模就只考虑小轿车的情况，根据小轿车的长度差距不大，对相关因素进行分析，从而可以作出有利于建立模型、基本符合实际情况的假设即可.
【详解】根据题意可知和相关因素的分析，可以作出有利于建立模型、基本符合实际情况的假设，例如①等待时，前后相邻两辆车的车距都相等；
②绿灯亮后，汽车都是在静止状态下匀加速启动；
③前一辆车启动后，下一辆车启动的延时时间相等；
④车辆行驶秩序良好，不会发生堵塞，等等；
故答案为：等待时，前后相邻两辆车的车距都相等（不唯一）.
四、解答题
15．（2024高三·全国·专题练习）某科研团队在培养基中放入一定量的某种细菌进行研究．经过2分钟菌落的覆盖面积为48 mm2，经过3分钟覆盖面积为64 mm2，后期其蔓延速度越来越快；菌落的覆盖面积y（单位：mm2）与经过时间x（单位：min）的关系现有三个函数模型：①y＝kax（k＞0，a＞1）；②y＝lgbx（b＞1）；③y＝p＋q（p＞0）可供选择．（参考数据：lg 2≈0.301，lg 3≈0.477）
(1)选出你认为符合实际的函数模型，说明理由，并求出该模型的解析式．
(2)在理想状态下，至少经过多少分钟培养基中菌落的覆盖面积能超过300 mm2？（结果保留到整数）
【答案】(1)应选函数模型y＝kax（k＞0，a＞1），y＝27×（）x（x≥0）
(2)9 min
【详解】解：（1）因为y＝kax（k＞0，a＞1）的增长速度越来越快，
y＝lgbx（b＞1）和y＝p＋q（p＞0）的增长速度越来越慢，
所以应选函数模型y＝kax（k＞0，a＞1）.
由题意得解得
所以该函数模型为y＝27×（）x（x≥0）.
（2）由题意得27×（）x＞300，即（）x＞，所以x＞lg.
又lg＝＝≈≈8.368，
所以至少经过9 min培养基中菌落的覆盖面积能超过300 mm2.
16．（2024高三·全国·专题练习）为了节能环保、节约材料，定义建筑物的“体形系数” ，其中为建筑物暴露在空气中的面积（单位：平方米），为建筑物的体积（单位：立方米）．
(1)若有一个圆柱体建筑的底面半径为，高度为，暴露在空气中的部分为上底面和侧面，试求该建筑体的“体形系数” ；（结果用含、的代数式表示）
(2)定义建筑物的“形状因子”为，其中为建筑物底面面积，为建筑物底面周长，又定义为总建筑面积，即为每层建筑面积之和（每层建筑面积为每一层的底面面积）．设为某宿舍楼的层数，层高为3米，则可以推导出该宿舍楼的“体形系数”为．当，时，试求当该宿舍楼的层数为多少时，“体形系数”最小．
【答案】(1)
(2)
【分析】（1）根据圆柱体的表面积和体积公式及求出答案；
（2）表达出，，构造函数，求导得到其单调性，进而得到S的最小值在或7取得，代入比较后得到结论.
【详解】（1）由圆柱体的表面积和体积公式可得：，，
所以；
（2）由题意可得，，
令，，
所以，
令，解得，
所以在单调递减，在单调递增，
所以S的最小值在或7取得，
当时，，
当时，，
所以在时，该建筑体S最小．
17．（2024·浙江金华·模拟预测）太阳能板供电是节约能源的体现，其中包含电池板和蓄电池两个重要组件，太阳能板通过电池板将太阳能转换为电能，再将电能储存于蓄电池中．已知在一定条件下，入射光功率密度（E为入射光能量且为入射光入射有效面积），电池板转换效率与入射光功率密度成反比，且比例系数为k．
(1)若平方米，求蓄电池电能储存量Q与E的关系式；
(2)现有铅酸蓄电池和锂离子蓄电池两种蓄电池可供选择，且铅酸蓄电池的放电量，锂离子蓄电池的放电量．设，给定不同的Q，请分析并讨论为了使得太阳能板供电效果更好，应该选择哪种蓄电池？
注：①蓄电池电能储存量；
②当S，k，Q一定时，蓄电池的放电量越大，太阳能板供电效果越好．
【答案】(1)
(2)答案见解析
【分析】（1）利用题目所给公式及数据计算即可得；
（2）用S，k，Q表示出两种蓄电池的放电量后作差比大小即可得.
【详解】（1），
若平方米，则；
（2）由，即，
铅酸蓄电池的放电量为：，
锂离子蓄电池的放电量为：，
则
，
令，可得，
即时，，此时应选择铅酸蓄电池，
当时，，此时应选择锂离子蓄电池，
当时，，两种电池都可以.
18．（2024·四川南充·二模）已知某科技公司的某型号芯片的各项指标经过全面检测后，分为Ⅰ级和Ⅱ级，两种品级芯片的某项指标的频率分布直方图如图所示：
若只利用该指标制定一个标准，需要确定临界值K，按规定须将该指标大于K的产品应用于A型手机，小于或等于K的产品应用于B型手机．若将Ⅰ级品中该指标小于或等于临界值K的芯片错误应用于A型手机会导致芯片生产商每部手机损失800元；若将Ⅱ级品中该指标大于临界值K的芯片错误应用于B型手机会导致芯片生产商每部手机损失400元；假设数据在组内均匀分布，以事件发生的频率作为相应事件发生的概率．
(1)设临界值时，将2个不作该指标检测的Ⅰ级品芯片直接应用于A型手机，求芯片生产商的损失（单位：元）的分布列及期望；
(2)设且，现有足够多的芯片Ⅰ级品、Ⅱ级品，分别应用于A型手机、B型手机各1万部的生产：
方案一：将芯片不作该指标检测，Ⅰ级品直接应用于A型手机，Ⅱ级品直接应用于B型手机；
方案二：重新检测该芯片Ⅰ级品，Ⅱ级品的该项指标，并按规定正确应用于手机型号，会避免方案一的损失费用，但检测费用共需要130万元；
请求出按方案一，芯片生产商损失费用的估计值（单位：万元）的表达式，并从芯片生产商的成本考虑，选择合理的方案．
【答案】(1)分布列见解析，
(2)，，方案二
【分析】（1）首先求出Ⅰ级品中该指标小于或等于的频率，依题意的可能取值为，，，求出所对应的概率，即可得到分布列与数学期望；
（2）首先求出Ⅰ级品该指标小于或等于临界值的频率，Ⅱ级品中该指标大于或等于临界值K的频率，即可求出损失费用的估计值的解析式，再求出值域，即可判断.
【详解】（1）当临界值时，Ⅰ级品中该指标小于或等于的频率为，
所以将个不作该指标检测的Ⅰ级品芯片直接应用于型手机，每部手机损失元的概率为，
所以芯片生产商的损失的可能取值为，，，
所以，，
，
所以的分布列为：
所以.
（2）当临界值且时，
若采用方案一：
Ⅰ级品中该指标小于或等于临界值的频率为，
所以可以估计部型手机中有部手机芯片应用错误；
Ⅱ级品中该指标大于或等于临界值的频率为，
所以可以估计部型手机中有部手机芯片应用错误；
所以可以估计芯片生产商的损失费用，
即，，
因为，所以，
又采用方案二需要检测费用共万元，
故从芯片生产商的成本考虑，应选择方案二.
19．（2024高三·全国·专题练习）将连续正整数1，2，，从小到大排列构成一个数，为这个数的位数如当时，此数为123456789101112，共有15个数字，，现从这个数中随机取一个数字，为恰好取到0的概率.
(1)求
(2)当时，求的表达式.
(3)令为这个数中数字0的个数，为这个数中数字9的个数，，，求当时的最大值.
【答案】(1)
(2)
(3)
【分析】（1）计算，数字0的个数为11，得到概率.
（2）考虑，，，四种情况，依次计算得到答案.
（3）考虑时，当时，当时三种情况，得到和的解析式，得到，再计算概率的最值得到答案.
【详解】（1）当时，，
即这个数中共有个数字，其中数字的个数为，
则恰好取到的概率为；
（2）当时，这个数有位数组成，；
当时，这个数有个一位数组成，个两位数组成，则；
当时，这个数有个一位数组成，个两位数组成，个三位数组成，；
当时，这个数有个一位数组成，个两位数组成，个三位数组成个四位数组成，；
综上所述：，
（3）当时，，
当时，；
当时，，
即，
同理有，
由，可知，
所以当时，，
当时，，
当时，，
当时，，
由关于单调递增，
故当时，有的最大值为，
又，
所以当时，的最大值为．
【点睛】关键点点睛：函数的解析式，概率的计算，最值问题，意在考查学生的计算能力，转化能力和综合应用能力，其中分类讨论的思想是解题的关键
拓展冲刺练
一、单选题
1．（2023·浙江·二模）绍兴某乡村要修建一条100米长的水渠，水渠的过水横断面为底角为120°的等腰梯形（如图）水渠底面与侧面的修建造价均为每平方米100元，为了提高水渠的过水率，要使过水横断面的面积尽可能大，现有资金3万元，当过水横断面面积最大时，水果的深度（即梯形的高）约为（ ）（参考数据：）
A．0.58米B．0.87米C．1.17米D．1.73米
【答案】B
【分析】如图设横截面为等腰梯形，于，求出资金3万元都用完时，设，再根据梯形的面积公式结合二次函数的性质即可得解.
【详解】如图设横截面为等腰梯形，于，，
要使水横断面面积最大，则此时资金3万元都用完，
则，解得米，
设，则，故，且，
梯形的面积，
当时，，
此时，
即当过水横断面面积最大时，水果的深度（即梯形的高）约为0.87米.
故选：B.
2．（2024·全国·模拟预测）北斗卫星导航系统是中国自行研制的全球卫星导航系统．已知卫星运行轨道近似为以地球为圆心的圆形，运行周期与轨道半径之间关系为（K为常数）．已知甲、乙两颗卫星的运行轨道所在平面互相垂直，甲的周期是乙的8倍，且甲的运行轨道半径为，分别是甲、乙两颗卫星的运行轨道上的动点，则之间距离的最大值为（ ）
A．B．
C．D．
【答案】B
【分析】根据题设条件得到，再根据图形，利用，当且仅当三点共线时取等号即可求出结果.
【详解】如图，设卫星乙的运行轨道半径为，因为，且，所以，
设地球的球心为，则，当且仅当与共线且位于两侧时取得等号，
故选：B．
3．（2024·全国·模拟预测）药物的半衰期指的是血液中药物浓度降低一半所需要的时间，在特定剂量范围内，药物的半衰期，其中是药物的消除速度常数，不同药物的消除速度常数一般不同，若内药物在血液中浓度由降低到，则该药物的消除速度常数．已知某药物半衰期为，首次服用后血药浓度为，当血药浓度衰减到时需要再次给药，则第二次给药与首次给药时间间隔约为（ ）
A．B．C．D．
【答案】B
【分析】由题意结合对数运算即可得.
【详解】因为，所以，
由题意，得，
所以．
故选：B.
4．（23-24高三上·湖北·阶段练习）已知把物体放在空气中冷却时，若物体原来的温度是，空气的温度是，则后物体的温度满足公式（其中是一个随着物体与空气的接触状况而定的正常数）.某天小明同学将温度是的牛奶放在空气中，冷却后牛奶的温度是，则下列说法正确的是（ ）
A．
B．
C．牛奶的温度降至还需
D．牛奶的温度降至还需
【答案】D
【分析】运用代入法，结合对数的运算逐一判断即可.
【详解】由，得，
即，故，A、B错误；
又由，，得，
故牛奶的温度从降至需，
从降至还需.
故选：D
5．（2024·陕西咸阳·模拟预测）某军区红、蓝两方进行战斗演习，假设双方兵力（战斗单位数）随时间的变化遵循兰彻斯特模型：，其中正实数，分别为红、蓝两方的初始兵力，为战斗时间；，分别为红、蓝两方时刻的兵力；正实数，分别为红方对蓝方、蓝方对红方的战斗效果系数；和分别为双曲余弦函数和双曲正弦函数．规定：当红、蓝两方任何一方兵力为0时战斗演习结束，另一方获得战斗演习胜利，并记战斗持续时长为．则下列结论不正确的是（ ）
A．若且，则
B．若且，则
C．若，则红方获得战斗演习胜利
D．若，则红方获得战斗演习胜利
【答案】C
【分析】对于A根据已知条件利用作差法比较大小即可得出，对于B，利用A中结论可得蓝方兵力先为0，即解得；对于C和D，若要红方获得战斗演习胜利，分别解出红、蓝两方兵力为0时所用时间、，比较大小即可.
【详解】对于A，若且，则，
即，所以，
由可得，即A正确；
对于B，当时根据A中的结论可知，所以蓝方兵力先为，
即，化简可得，
即，两边同时取对数可得，
即，所以战斗持续时长为，所以B正确；
对于C，若红方获得战斗演习胜利，则红方可战斗时间大于蓝方即可，
设红方兵力为时所用时间为，蓝方兵力为时所用时间为，
即，可得
同理可得，即，解得，
又因为都为正实数，所以可得，红方获得战斗演习胜利；
所以可得C错误，D正确.
故选：C.
【点睛】关键点点睛：本题给的信息比较多，关键是理解题意，然后利用相应的知识（作差法、指数函数的性质）进行判断.
二、多选题
6．（23-24高三下·重庆·阶段练习）吸光度是指物体在一定波长范围内透过光子的能量占收到光能量的比例.透光率是指光子通过物体的能量占发出光能量的比例.在实际应用中，通常用吸光度和透光率来衡量物体的透光性能，它们之间的换算公式为，如表为不同玻璃材料的透光率：
设材料1､材料2､材料3的吸光度分别为，则（ ）
A．B．
C．D．
【答案】BCD
【分析】由对数式与指数式的互化，得，由的值，结合对数式的运算规则和对数函数的单调性，判断选项中的不等式是否成立.
【详解】由，得，则，，，
，，，即，A选项错误；
，B选项正确；
，C选项正确；
，，
，
，
，
所以，则有，
又，则，D选项正确；
故选：BCD
7．（22-23高三上·重庆万州·阶段练习）某摩天轮共有32个乘坐舱，按旋转顺序依次为1~33号（因忌讳，没有13号），并且每相邻两个乘坐舱与旋转中心所成的圆心角均相等，已知乘客在乘坐舱距离底面最近时进入，在后距离地面的高度，已知该摩天轮的旋转半径为60m，最高点距地面135m，旋转一周大约30min，现有甲乘客乘坐11号乘坐舱，当甲乘坐摩天轮15min时，乙距离地面的高度为，则乙所乘坐的舱号为（ ）
A．6B．7C．15D．16
【答案】BD
【分析】先由最小正周期求出，进而由最高点和最低点与地面的距离求出，由甲乘坐摩天轮15min时，距底面为最大高度，求出，得到解析式，令求出min或min，求出每相邻两个乘坐舱旋转到同一高度的时间间隔，分别求出min和min时，甲乙相差的乘坐舱个数，得到答案.
【详解】由题意得：min，故，
摩天轮最低点距底面m，
故，解得：，
故，
由于min，故甲乘坐摩天轮15min时，距地面为最大高度，
即，
故，
因为，所以，故，
解得：，
故，
令，其中，
解得：，
令，，解得：，，
因为，所以，解得：，
此时
令，，解得：，，
因为，所以，解得：，
此时
综上：min或min，
每相邻两个乘坐舱与旋转中心所成的圆心角为，故每相邻两个乘坐舱旋转到同一高度的时间间隔为，
当min时，乙比甲晚出发min，甲乙相差个乘坐舱，
由于没有13号乘坐舱，故乙在16号乘坐舱，
当min时，乙比甲早出发min，甲乙相差个乘坐舱，
故乙在7号乘坐舱.
故选：BD
三、填空题
8．（2023高三上·全国·专题练习）考古学家对四川广汉“三星堆古墓”进行考古发据，科学家通过古生物中某种放射性元素的存量来估算古生物的年代，已知某放射性元素的半衰期约为4200年（即：每经过4200年，该元素的存量为原来的一半），已知古生物中该元素的初始存量为a，经检测古生物中该元素现在的存量为，请推算古生物距今大约 年（参考数据：lg2≈0.3）.
【答案】5600
【分析】根据给定条件，求出元素的存量y与时间x（年）的关系式，列出方程并结合对数运算即得结果.
【详解】由半衰期的定义可知，每年古生物中该元素的存量是上一年该元素存量的，
因此该元素的存量y与时间x（年）的关系式为，x≥0，
由，得，则，
解得≈5600，
所以该古生物距今大约5600年.
故答案为：5600
9．（2023·北京·模拟预测）农业技术员进行某种作物的种植密度试验，把一块试验田划分为8块面积相等的区域（除了种植密度，其它影响作物生长的因素都保持一致），种植密度和单株产量统计如下：

根据上表所提供信息，第 号区域的总产量最大．
【答案】5
【分析】分别求出种植密度函数和单株产量函数的解析式，再求总产量的函数解析式，由此确定其最大值及取最大值的条件即可.
【详解】设区域代号为，种植密度为，单株产量为，则，
由图象可得种植密度是区域代号的一次函数，
故设，，
由已知函数的图象经过点,，
所以，解得，
所以，
由图象可得单株产量是区域代号的一次函数，
故可设，，
观察图象可得当时，，当时，，
所以，解得，
所以，
所以总产量
当时，函数有最大值，即号区域总产量最大，最大值为.
故答案为：5.
四、解答题
10．（2024高三·全国·专题练习）随着神舟十五号载人飞船顺利发射，人们对航天事业愈发关注，航天周边产品销量也逐渐提高．某商场准备购进一批火箭模型进行售卖，已知一个B款火箭模型比一个A款贵15元，用1 600元购入的A款火箭模型与2 200元购入的B款火箭模型数量相同．
(1)这两款火箭模型的进货单价各是多少元？
(2)已知商场准备购进这两款火箭模型共100个，后将这批火箭模型以A款每个70元，B款每个90元的价格出售．求可获得的总利润y(元)与其中A款火箭模型的数量x(个)之间的关系式．
【答案】(1)A款火箭模型的进价为40元，B款火箭模型的进价为55元
(2)
【详解】（1）设一个A款火箭模型的进价为x元，
则一个B款火箭模型的进价为(x＋15)元，
则有＝，解得x＝40，经检验，x＝40是原方程的解，
所以A款火箭模型的进价为40元，B款火箭模型的进价为55元．
（2）因为A款火箭模型的数量为x个，
则B款火箭模型的数量为(100－x)个，
所以y＝(70－40)x＋(90－55)(100－x)＝3 500－5x(0≤x≤100).
11．（2024·山东·模拟预测）如图①，将个完全一样质量均匀长为的长方体条状积木，一个叠一个，从桌子边缘往外延伸，最多能伸出桌缘多远而不掉下桌面呢？这就是著名的“里拉斜塔问题”．
解决方案如下：如图②，若，则当积木与桌缘垂直且积木重心恰与桌缘齐平时，其伸出桌外部分最长为，如图③，若，欲使整体伸出桌缘最远，在保证所有积木最长棱与桌缘垂直的同时，可先将上面积木的重心与最下方的积木伸出桌外的最远端齐平，然后设最下方积木伸出桌外的长度为，将最下方积木看成一个杠杆，将桌缘看成支点，由杠杆平衡原理可知，若积木恰好不掉下桌面，则上面积木的重力乘以力臂，等于最下方积木的重力乘以力臂，得出方程，求出．所以当叠放两个积木时，伸出桌外最远为，此时将两个积木看成整体，其重心恰与桌缘齐平．如图④，使前两块积木的中心与下方的第三块积木伸出桌外的最远端齐平，便可求出时积木伸出桌外的最远距离．依此方法，可求出4个、5个直至个积木堆叠伸出桌外的最远距离．（参考数据：，为自然常数）
(1)分别求出和时，积木伸出桌外的最远距离．（用表示）；
(2)证明：当时，积木伸出桌外最远超过；
(3)证明：当时，积木伸出桌外最远不超过．
【答案】(1)当时，最远距离为，当时，最远距离为
(2)证明见解析
(3)证明见解析
【分析】（1）将前个看成一个整体，结合题意列式计算即可得；
（2）将前个看成一个整体，设第个积木伸出桌外的长度为，可得，即有当时，积木堆叠伸出桌外的最远距离为，构造函数，结合导数研究函数单调性可得，即可得，将代入即可得证；
（3）构造函数，结合导数研究函数单调性可得，故有，将代入即可得证.
【详解】（1）当时，有，则，，
当时，有，则，故，
故当时，积木伸出桌外的最远距离为，
当时，积木伸出桌外的最远距离为，
（2）当个积木堆叠伸出桌外时，前个看成一个整体，
设第个积木伸出桌外的长度为，则有，解得，
故当时，积木堆叠伸出桌外的最远距离为：
，
令，则，
故在上单调递增，故，
令，则有，即，
故，
即，又，故，
故，
即当时，积木伸出桌外最远超过；
（3）由（2）知，当时，积木堆叠伸出桌外的最远距离为：
，
令，
则，
故在上单调递增，故，
即有在上恒成立，
令，则有，
故，
即，则，
要证当时，积木伸出桌外最远不超过，
只需证， 即证，
由，故，
即只需证，由，
故，即得证.
【点睛】关键点点睛：本题关键点有两个，一个是由题意得到第个积木伸出桌外的长度为时，有，可得，即可得个积木堆叠伸出桌外的最远距离为，第二个是证明（2）、（3）问时，构造对应函数及，通过研究函数单调性，得到及.
函数
性质
y＝ax(a>1)
y＝lgax(a>1)
y＝xn(n>0)
在(0，＋∞)上的增减性
单调递增
单调递增
单调递增
增长速度
越来越快
越来越慢
相对平稳
图象的变化
随x的增大逐渐表现为与y轴平行
随x的增大逐渐表现为与x轴平行
随n值的变化而各有不同
函数模型
函数解析式
一次函数模型
f(x)＝ax＋b(a，b为常数，a≠0)
二次函数模型
f(x)＝ax2＋bx＋c(a，b，c为常数，a≠0)
反比例函数模型
f(x)＝eq \f(k,x)＋b(k，b为常数，k≠0)
指数函数模型
f(x)＝bax＋c(a，b，c为常数，a>0且a≠1，b≠0)
对数函数模型
f(x)＝blgax＋c(a，b，c为常数，a>0且a≠1，b≠0)
幂函数模型
f(x)＝axα＋b(a，b，α为常数，a≠0，α≠0)
甲
乙
丙
接单量t（单）
7831
8225
8338
油费s（元）
107150
110264
110376
平均每单里程k（公里）
15
15
15
平均每公里油费a（元）
0.7
0.7
0.7
10
20
30
40
50
60
70
80
12.8
16.5
19
20.9
21.5
21.9
23
25.4
161
29
20400
109
603
出险情况
商业险折扣
若基准保费3000元时对应保费
三年内6赔
1.8
5400
三-年内5赔
1.5
4500
三年内4赔
1.2
3600
三年内3赔
1
3000
三年内2赔
0.8
2400
三年内1赔
0.7
2100
三年内0赔
0.6
1800
物质
τ的量纲单位
τ的值
铀234
万年
35.58
铀235
亿年
10.2
铀238
亿年
64.75
玻璃材料
材料1
材料2
材料3
0.6
0.7
0.8