2025年新高考数学精析考点考点29解三角形及其应用举例(2种核心题型+基础保分练+综合提升练+拓展冲刺练)(原卷版+解析)

这是一份2025年新高考数学精析考点考点29解三角形及其应用举例(2种核心题型+基础保分练+综合提升练+拓展冲刺练)(原卷版+解析)，文件包含2025年新高考数学精析考点考点29解三角形及其应用举例2种核心题型+基础保分练+综合提升练+拓展冲刺练原卷版docx、2025年新高考数学精析考点考点29解三角形及其应用举例2种核心题型+基础保分练+综合提升练+拓展冲刺练解析版docx等2份试卷配套教学资源，其中试卷共81页， 欢迎下载使用。
1.能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题
2.能利用正弦定理、余弦定理解决三角形中的最值和范围问题.
3.通过解决实际问题，培养学生的数学建模、直观想象和数学运算素养．
【知识点】
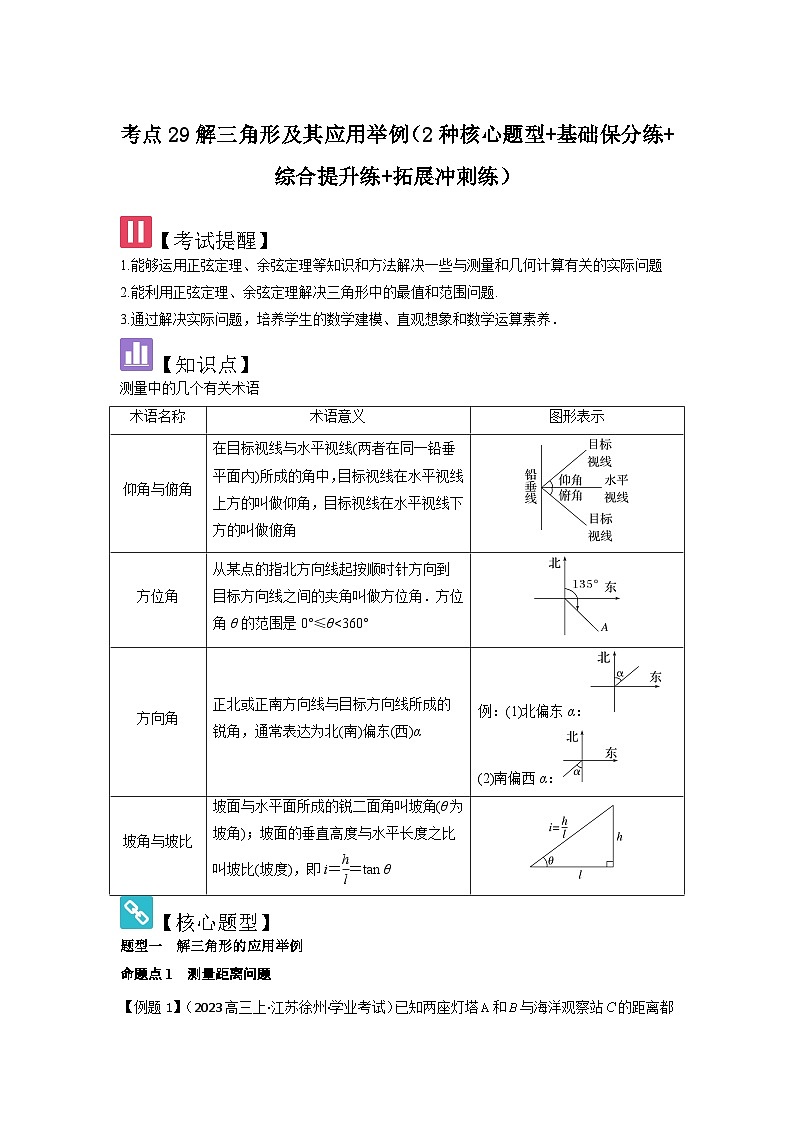
测量中的几个有关术语
【核心题型】
题型一 解三角形的应用举例
命题点1 测量距离问题
【例题1】（2023高三上·江苏徐州·学业考试）已知两座灯塔和与海洋观察站的距离都等于，灯塔在观察站的北偏东，灯塔在观察站的南偏东，则灯塔与灯塔的距离为（）
A．B．C．D．
【答案】D
【分析】利用余弦定理求得正确的.
【详解】依题意，
所以.
故选：D
【变式1】（2023·河南郑州·模拟预测）如图，某景区为方便游客，计划在两个山头M，N间架设一条索道．为测量M，N间的距离，施工单位测得以下数据：两个山头的海拔高度，在BC同一水平面上选一点A，测得M点的仰角为，N点的人仰角为，以及， 则M，N间的距离为（ ）

A．B．120mC．D．200m
【答案】A
【分析】根据题意，在直角和直角中，分别求得和，再在中，利用余弦定理，即可求解.
【详解】由题意，可得，
且，
在直角中，可得，
在直角中，可得，
在中，由余弦定理得，
所以.
故选：A.
【变式2】（2022·山东青岛·二模）如图所示，A，B，C为三个村庄，，，，则 ；若村庄D在线段BC中点处，要在线段AC上选取一点E建一个加油站，使得该加油站到村庄A，B，C，D的距离之和最小，则该最小值为 .
【答案】 60°/ /
【分析】利用余弦定理以及点关于线的对称点进行处理.
【详解】在中，由余弦定理有：

又，所以.
如图，作D关于AC的对称点F，则DE=FE，DC=FC=4，
，所以，当且仅当
B，E，F三点共线时，BE+EF最小.
.
所以，所以AE+CE+BE+DE=AC+BE+EF，
当且仅当B，E，F三点共线时，等号成立.
故答案为：，.
【变式3】（2023高三上·全国·专题练习）如图，A、B两点都在河的对岸(不可到达)，若在河岸选取相距20米的C、D两点，测得∠BCA＝60°，∠ACD＝30°，∠CDB＝45°，∠BDA＝60°，那么此时A，B两点间的距离是多少？
【答案】米
【分析】根据正弦定理，分别在和中求出AC，BC，然后在中，由余弦定理求得AB.
【详解】根据正弦定理，
在中，有(米)，
在中，有(米)．
在中，由余弦定理得AB＝＝(米)．
所以A，B两点间的距离为米
命题点2 测量高度问题
【例题2】（2024·广东·二模）在一堂数学实践探究课中，同学们用镜而反射法测量学校钟楼的高度.如图所示，将小镜子放在操场的水平地面上，人退后至从镜中能看到钟楼顶部的位置，此时测量人和小镜子的距离为，之后将小镜子前移，重复之前的操作，再次测量人与小镜子的距离为，已知人的眼睛距离地面的高度为，则钟楼的高度大约是（ ）

A．B．C．D．
【答案】D
【分析】设钟楼的高度为，根据相似得到，代入数据计算得到答案.
【详解】如下图，设钟楼的高度为，
由，可得：，
由，可得：，
故，
故，
故选：D.

【变式1】（2024·湖南岳阳·二模）岳阳楼地处岳阳古城西门城墙之上，下瞰洞庭，前望君山．因范仲淹的《岳阳楼记》著称于世，自古有“洞庭天下水，岳阳天下楼”之美誉．小明为了测量岳阳楼的高度，他首先在处，测得楼顶的仰角为，然后沿方向行走22.5米至处，又测得楼顶的仰角为，则楼高为 米．
【答案】
【分析】在中，用表示，在中，用表示，根据的长，可求解.
【详解】中，，，，
中，，，，
因为米，所以，
解得：
故答案为：
【变式2】（2024·广东湛江·二模）财富汇大厦坐落在广东省湛江市经济技术开发区，是湛江经济技术开发区的标志性建筑，同时也是已建成的粤西第一高楼.为测量财富汇大厦的高度，小张选取了大厦的一个最高点A，点A在大厦底部的射影为点O，两个测量基点B、C与O在同一水平面上，他测得米，，在点B处测得点A的仰角为（），在点C处测得点A的仰角为45°，则财富汇大厦的高度 米.
【答案】204
【分析】根据仰角设出长度，再根据余弦定理列出的边长关系，解方程求解即可.
【详解】设米，因为在点B处测得点A的仰角为，所以，所以.
因为在点C处测得点A的仰角为45°，所以米.
由余弦定理，可得，
即，解得.
故答案为：204
【变式3】（2022·贵州安顺·模拟预测）如图，为测量某雕像AB的高度（B，C，D，F在同一水平面上，雕像垂直该水平面于点B，且B，C，D三点共线），某校研究性学习小组同学在C，D，F三点处测得顶点A的仰角分别为，，，米．

(1)求雕像AB的高度；
(2)当观景点C与F之间的距离为多少米时，△CDF的面积最大？并求出最大面积．
【答案】(1)
(2)时，的面积最大，最大值为
【分析】（1）根据已知条件，在中，可求出.然后在中，根据已知即可求得答案；
（2）根据（1）可求出.由已知可得出.进而根据面积公式表示出的面积.即可得出面积的最大值以及，由勾股定理即可求出.
【详解】（1）由已知可得，
在中，有，，，
所以，，
所以，为等腰三角形，.
在中，有，，，
所以，，
所以，.
（2）由（1）可得，，
在中，，所以.
因为的边上的高，
且的边上的高也等于，
所以的面积为.
当，即时，面积最大，最大值为.
此时有.
命题点3 测量角度问题
【例题3】（2024·上海嘉定·二模）嘉定某学习小组开展测量太阳高度角的数学活动．太阳高度角是指某时刻太阳光线和地平面所成的角．测量时，假设太阳光线均为平行的直线，地面为水平平面．如图，两竖直墙面所成的二面角为120°，墙的高度均为3米．在时刻，实地测量得在太阳光线照射下的两面墙在地面的阴影宽度分别为1米、1.5米．在线查阅嘉定的天文资料，当天的太阳高度角和对应时间的部分数据如表所示，则时刻最可能为（ ）
A．B．C．D．
【答案】B
【分析】作出示意图形，在四边形中利用正弦定理与余弦定理，算出四边形的外接圆直径大小，然后在中利用锐角三角函数定义，算出的大小，即可得到本题的答案.
【详解】如图所示，
设两竖直墙面的交线为，点被太阳光照射在地面上的影子为点，
点分别是点在两条墙脚线上的射影，连接 ，，，
由题意可知就是太阳高度角.
∵四边形中，，，
∴ ，
∴中，，
可得，
∵四边形是圆内接四边形，是其外接圆直径，
∴设的外接圆半径为，则，
在中，，
所以，
对照题中表格，可知时刻时，太阳高度角为，与最接近.
故选：B.
【变式1】（2023·四川绵阳·三模）《孔雀东南飞》中曾叙“十三能织素，十四学裁衣，十五弹箜篌，十六诵诗书.”箜篌历史悠久、源远流长，音域宽广、音色柔美清撤，表现力强.如图是箜篌的一种常见的形制，对其进行绘制，发现近似一扇形，在圆弧的两个端点，处分别作切线相交于点，测得切线，，，根据测量数据可估算出该圆弧所对圆心角的余弦值为（ ）
A．0.62B．0.56C．D．
【答案】A
【分析】由图形可知，由余弦定理求出，可得.
【详解】由题意，，所以，
切线，，由切线长定理，不妨取，
又，由余弦定理，
有， .
故选：A
【变式2】（2023·河北·模拟预测）如图是一款订书机，其内部结构可简化为如图模型.使用时将B下压，E接触平台，D紧邻E，此时钝角增大了（ ）（参考数据：，，.）
A．B．C．D．
【答案】D
【分析】根据题意结合余弦定理运算求解.
【详解】如图1，过点A作，，垂足为，，则，
故，
连接，在中，由余弦定理可得：，即，
∵，即此时为锐角，
如图2 ，设平台，即三点重合，则，
连接，在中，由余弦定理可得：，
在中，由余弦定理可得：，
则，
整理得，即，
又∵，则，
此时钝角增大的值大于，符合题意的只有D选项.
故选：D.
【变式3】（2022·河北衡水·模拟预测）瀑布是庐山的一大奇观，唐代诗人李白曾在《望庐山瀑布中》写道：日照香炉生紫烟，遥看瀑布挂前川，飞流直下三千尺，疑是银河落九天.为了测量某个瀑布的实际高度，某同学设计了如下测量方案：沿一段水平山道步行至与瀑布底端在同一水平面时，在此位置测得瀑布顶端的仰角正切值为，沿山道继续走20，测得瀑布顶端的仰角为.已知该同学沿山道行进的方向与他第一次望向瀑布底端的方向所成角为.根据这位同学的测量数据，可知该瀑布的高度为 ；若第二次测量后，继续行进的山道有坡度，坡角大小为，且两段山道位于同一平面内，若继续沿山道行进，则该同学望向瀑布顶端与底端的视角正切值为 .（此人身高忽略不计）
【答案】 60 3
【分析】根据题意画出图形，设高度为，则可表示出，在中利用余弦
定理即可求出的值；由已知数据易知，则，则可得到
，再由两角和的正切公式计算出结果.
【详解】如图，设瀑布顶端为，底端为，高为，
该同学第一次测量的位置为，第二次测量的位置为，
则，,
所以，
在中由余弦定理可知：
即，
解得：;
如图，两段山道为,过作于点，
由题意知：，，
所以，
在中，即，
所以，
所以，
所以，
又，
所以，
，
所以.
故答案为：60；3.
题型二 解三角形中的最值和范围问题
解三角形中最值(范围)问题的解题策略
利用正弦、余弦定理以及面积公式化简整理，构造关于某一个角或某一条边的函数或不等式，利用函数的单调性或基本不等式等求最值(范围)．
【例题4】（2024·江西南昌·三模）如图，在扇形OAB中，半径，，C在半径OB上，D在半径OA上，E是扇形弧上的动点（不包含端点），则平行四边形BCDE的周长的取值范围是（ ）
A．B．
C．D．
【答案】A
【分析】由于点E在弧上运动，引入恰当的变量，从而表达，再利用正弦定理来表示边，来求得周长关于角的函数，然后求出取值范围；也可以建立以圆心为原点的坐标系，同样设出动点坐标，用坐标法求出距离，然后同样把周长转化为关于角的函数，进而求出取值范围.
【详解】
（法一）如图，连接设，则，，
故．在中，由正弦定理可得，
则．
在中，由正弦定理可得，则．
平行四边形的周长为
．
因为，所以，所以，所以，
所以，则，
即平行四边形BCDE的周长的取值范围是．
（法二）以O为原点，所在直线分别为x，y轴，建立平面直角坐标系．
设，则，，
从而，，，
，
故平行四边形的周长为．
因为，所以，所以，
则，即平行四边形的周长的取值范围是．
故选：A.
【变式1】（2024·重庆·模拟预测）已知的内角所对的边分别为，满足，，且，则边 ．
【答案】
【分析】利用正弦定理结合余弦定理可得，由面积公式可得，由正弦定理得，化简可得结果.
【详解】因为，由正弦定理可得：，
所以，由余弦定理可得：，
因为，所以，
因为，所以，
由正弦定理可得：，，
所以，即
故答案为：
【变式2】（2024·山西·三模）已知的内角A，B，C的对边分别为a，b，c，满足．
(1)试判断的形状；
(2)若的外接圆半径为2，求周长的最大值．
【答案】(1)为等腰三角形
(2)
【分析】（1）根据题意结合三角恒等变换可得，结合分析求解；
（2）利用正弦定理可得周长，构建函数，利用导数求最值，即可得结果.
【详解】（1）由题意可知：
，
整理得，
且，则，可知，即，
所以为等腰三角形.
（2）由正弦定理，可得，
则周长，
由（1）可知：，
可得，
构建函数，
则，
因为，则，
当时，，则；
当时，，则；
可知在内单调递增，在内单调递减，
则，
所以当且仅当为等边三角形时，周长取到最大值.
【变式3】（2024·山东济宁·三模）在△ABC中，角A，B，C所对的边分别为，已知.
(1)求证:；
(2)若，求面积的取值范围.
【答案】(1)证明见解析
(2)
【分析】（1）根据两角和差的正弦公式、二倍角的余弦公式化简计算可得，结合诱导公式计算即可证明；
（2）由（1）得且，根据正弦定理、三角形的面积公式和三角恒等变换化简可得，结合正切函数的性质即可求解.
【详解】（1），
，
，又，
则，
，
，即，
又，所以，即，
又，所以；
（2）由（1）知，，得，
由，得，由正弦定理得，
得，
所以，
又，所以，又在上单调递增，
则，所以，
即的面积我取值范围为.
【课后强化】
【基础保分练】
一、单选题
1．（2022·吉林·模拟预测）位于灯塔A处正西方向相距n mile的B处有一艘甲船需要海上救援，位于灯塔A处北偏东45°相距n mile的C处的一艘乙船前往营救，则乙船的目标方向线（由观测点看目标的视线）的方向是南偏西（ ）
A．30°B．60°C．75°D．45°
【答案】B
【分析】根据已知条件作出图形，找出要求的角为，运用解三角形的知识进行求解.
【详解】依题意，过点作的延长线交于点，如图，
则，，，
在中，，
在中，，，
又
，
则乙船的目标方向线（由观测点看目标的视线）的方向是南偏西60°.
故选：B.
2．（2024·内蒙古赤峰·模拟预测）为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度，通常采用人工攀登的方式进行，测量人员从山脚开始，直到到达山顶分段测量过程中，已知竖立在点处的测量觇标高米，攀登者们在处测得，到觇标底点和顶点的仰角分别为，则的高度差约为（ ）
A．7.32米B．7.07米C．27.32米D．30米
【答案】A
【分析】画出示意图，结合三角函数的定义和正切展开式求解即可.
【详解】
模型可简化为如上图，在中，，
所以，而，
代入上式并化简可得米，
故选：A.
3．（2024·云南昆明·一模）早期天文学家常采用“三角法”测量行星的轨道半径．假设一种理想状态：地球E和某小行星M绕太阳S在同一平面上的运动轨道均为圆，三个星体的位置如图所示．地球在位置时，测出；行星M绕太阳运动一周回到原来位置，地球运动到了位置，测出，．若地球的轨道半径为R，则下列选项中与行星M的轨道半径最接近的是（参考数据：）（ ）

A．B．C．D．
【答案】A
【分析】连接，根据给定条件，在中利用正弦定理求出，再在中利用余弦定理求解即得.
【详解】连接，在中，，又，则是正三角形，，
由，，得，，
在中，，由正弦定理得，则，
在中，由余弦定理得.
故选：A

4．（2024·陕西西安·模拟预测）在高的楼顶处，测得正西方向地面上两点与楼底在同一水平面上）的俯角分别是和，则两点之间的距离为（ ）．
A．B．C．D．
【答案】D
【分析】根据图形，利用直角三角形求解即可.
【详解】由题意，
而，
所以.
故选：D
二、多选题
5．（2023·重庆·三模）如图，为了测量障碍物两侧A，B之间的距离，一定能根据以下数据确定AB长度的是（ ）
A．a，b，B．，，
C．a，，D．，，b
【答案】ACD
【分析】由三角形全等的条件或者正、余弦定理即可判定.
【详解】法一、根据三角形全等的条件可以确定A、C、D三项正确，它们都可以唯一确定三角形；
法二、对于A项，由余弦定理可知，可求得，即A正确；
对于B项，知三个内角，此时三角形大小不唯一，故B错误；
对于C项，由正弦定理可知，即C正确；
对于D项，同上由正弦定理得，即D正确；
故选：ACD.
6．（2024·河北邯郸·三模）已知的三个内角A，B，C的对边分别是a，b，c，面积为，则下列说法正确的是（ ）
A．的取值范围是
B．若为边的中点，且，则的面积的最大值为
C．若是锐角三角形，则的取值范围是
D．若角的平分线与边相交于点，且，则的最小值为10
【答案】ABC
【分析】借助面积公式与余弦定理由题意可得，对A：借助三角恒等变换公式可将其化为正弦型函数，借助正弦型函数的单调性即可得；对B：借助向量数量积公式与基本不等式即可得；对C：借助正弦定理可将其化为与角有关的函数，结合角度范围即可得解；对D：借助等面积法及基本不等式计算即可得.
【详解】由题意知，整理得，
由余弦定理知，，，．
对A，
，
，，，
的取值范围为，故A正确；
对B，为边的中点，，
则，
，当且仅当时，等号成立，
，故B正确；
对于C，，
是锐角三角形，，
，，故C正确；
对于D，由题意得，
即，
整理得，即，
，
当且仅当时，等号成立，故D错误．
故选：ABC.
【点睛】关键点点睛：本题考查三角形中的最值与范围问题，主要思考方向有两个，一个是借助余弦定理得到边之间的关系，从而通过基本不等式求解，一个是借助正弦定理将边化为角，通过三角形中角的关系将多个变量角化为单变量，借助函数性质得到范围或最值.
三、填空题
7．（2022·全国·模拟预测）如图，为测量山高，选择A和另一座山的山顶C为测量观测点，从点A测得点M的仰角，点C的仰角，以及.从点C测得,已知山高，则山高 m.
【答案】
【分析】在中，求得，再在中，利用那个正弦定理，求得，进而在直角中，即可求解.
【详解】在中，因为，所以，
在中，因为，，可得，
因为，所以，
在直角中，可得.
故答案为：.
8．（2024·江苏扬州·模拟预测）《海岛算经》是魏晋时期数学家刘徽所著的测量学著作，书中有一道测量山上松树高度的题目，受此题启发，小李同学打算用学到的解三角形知识测量某建筑物上面一座信号塔的高度．把塔底与塔顶分别看作点C，D，CD与地面垂直，小李先在地面上选取点A，B，测得，在点A处测得点C，D的仰角分别为，，在点B处测得点D的仰角为，则塔高CD为 m．
【答案】20
【分析】确定每个角的大小，可得均为等腰三角形，在中，设，通过余弦定理计算即可.
【详解】在中，延长与的延长线交于点E，如图所示.
由题意可知，，
因为小李同学根据课本书中有一道测量山上松树高度的题目受此题启发，
所以三点在同一条直线上.
所以，
所以为等腰三角形，
即.
设，即，，
在中，由余弦定理得
,
即，，
所以，
又因为，
所以.
故答案为：.
9．（2024·宁夏·一模）在中，，，点D与点B分别在直线AC的两侧，且，，则BD的长度的最大值是 ．
【答案】
【分析】先判断为直角三角形，设，，由正弦定理得到与之间的数量关系，由余弦定理得到与之间的数量关系，最后在中，由余弦定理及所得结论得到，利用正弦型函数的值域即得BD的长度的最大值.
【详解】
如图，在中，由正弦定理：可得：，因，则，即.
设，则，在中，设，由正弦定理，，则得：，
由余弦定理可得：，即.
在中，由余弦定理，,
因，则，则当时，即时，，此时.
故答案为：.
【点睛】思路点睛：本题主要考查利用正、余弦定理求边长的最大值问题，属于难题.
解决此类题型的思路就是，要善于在图形中选设与已知条件和所求结论都相关的角，借助于正、余弦定理将所求量表示成关于角的三角函数式，最后根据三角函数的值域求得最值.
四、解答题
10．（2023·辽宁抚顺·模拟预测）如图，某乡镇绿化某一座山体，以地面为基面，在基面上选取A，B，C，D四个点，使得，测得，，．
(1)若B，D选在两个村庄，两村庄之间有一直线型隧道，且，，求A，C两点间距离；
(2)求的值．
【答案】(1)
(2)
【分析】（1）由正弦定理证得为等腰直角三角形，再由余弦定理求即可；
（2）设，利用正弦定理可得，展开化简即可得其正切值.
【详解】（1）在中，由正弦定理得，
即，
解得，所以，
则为等腰直角三角形，所以，
则．
在中，由余弦定理得
，
故．
故A，C两点间距离为．
（2）设，则由题意可知，，．
在中，由正弦定理得，即，
在中，由正弦定理得，即，
又，所以，
解得，所以．
11．（2024·四川·三模）三角形中，角的对边分别为，且 .
(1)求；
(2)若边上的中线长为2，求的最小值.
【答案】(1)
(2)
【分析】（1）利用二倍角的正余弦公式化简即可得解；
（2）利用向量化及余弦定理结合基本不等式即可得解.
【详解】（1）由，
得，即，
所以，即，
又，所以；
（2）设的中点为，
则，
平方得，即，
所以，当且仅当时取等号，
由余弦定理得，
因为，所以，
即的最小值为，当且仅当时取等号.
【综合提升练】
一、单选题
1．（2022·北京通州·一模）太阳高度角是太阳光线与地面所成的角（即太阳在当地的仰角）．设地球表面某地正午太阳高度角为，为此时太阳直射点纬度，为当地纬度值，那么这三个量满足．通州区某校学生科技社团尝试估测通州区当地纬度值（取正值），选择春分当日（）测算正午太阳高度角．他们将长度为1米的木杆垂直立于地面，测量木杆的影长．分为甲、乙、丙、丁四个小组在同一场地进行，测量结果如下：
则四组中对通州区当地纬度估测值最大的一组是（ ）
A．甲组B．乙组C．丙组D．丁组
【答案】D
【分析】根据题意得到，设木杆的影长为，得到，根据表格中的数据得到当时，取得最小值，此时求得最大值，即可求解.
【详解】如图所示，地球表面某地正午太阳高度角为，为此时太阳直射点纬度，为当地纬度值，那么这三个量满足，
当且为正值，可得，即，
设木杆的影长为，可得，
因为甲、乙、丙、丁四个小组在同一场地进行，得到影长分别为，
所以当时，取得最小值，此时求得最大值，
所以四组中对通州区当地纬度估测值最大的一组是丁组.
故选：D.
2．（2024·贵州·模拟预测）如图，甲秀楼位于贵州省贵阳市南明区甲秀路，是该市的标志性建筑之一.甲秀楼始建于明朝，后楼毁重建，改名“凤来阁”，清代甲秀楼多次重修，并恢复原名、现存建筑是宣统元年（1909年）重建.甲秀楼上下三层，白石为栏，层层收进.某研究小组将测量甲秀楼最高点离地面的高度，选取了与该楼底在同一水平面内的两个测量基点与，现测得，，，在点测得甲秀楼顶端的仰角为，则甲秀楼的高度约为（参考数据：，）（ ）
A．B．C．D．
【答案】C
【分析】利用正弦定理在中取得的长，根据正切函数的定，可得答案.
【详解】由题意可知，，，所以，又因，
由正弦定理，可得：，解得，
又因为，所以，
故选:C.
3．（2023·陕西宝鸡·二模）在锐角△ABC中，角A，B，C的对边分别为a，b，c，且，，则a的取值范围为（ ）
A．B．
C．D．
【答案】C
【分析】确定角范围后，由正弦定理表示出，再利用三角函数性质得结论．
【详解】因为是锐角三角形，所以，，所以，，
由正弦定理得，所以．
故选：C．
4．（2024·吉林·二模）如图，位于某海域处的甲船获悉，在其北偏东 方向处有一艘渔船遇险后抛锚等待营救. 甲船立即将救援消息告知位于甲船北偏东，且与甲船相距的处的乙船，已知遇险渔船在乙船的正东方向，那么乙船前往营救遇险渔船时需要航行的距离为（ ）
A．B．
C．D．
【答案】B
【分析】由图可知，由正弦定理即可求出BC的值.
【详解】由题意知，，
由正弦定理得，
所以.
故乙船前往营救遇险渔船时需要航行的距离为.
故选：B.
5．（2024·湖南·模拟预测）湖南省衡阳市的来雁塔，始建于明万历十九年（1591年），因鸿雁南北迁徙时常在境内停留而得名.1983年被湖南省人民政府公布为重点文物保护单位.为测量来雁塔的高度，因地理条件的限制，分别选择C点和一建筑物DE的楼顶E为测量观测点，已知点A为塔底，在水平地面上，来雁塔AB和建筑物DE均垂直于地面（如图所示）.测得，在C点处测得E点的仰角为30°，在E点处测得B点的仰角为60°，则来雁塔AB的高度约为（ ）（，精确到）
A．B．C．D．
【答案】B
【分析】现从四棱锥中提取两个直角三角形和的边角关系，进而分别解出两个三角形边的长，求出来雁塔AB的高度即可.
【详解】过点作，交于点，
在直角三角形中，因为，
所以，
在直角三角形中，因为，
所以，
则.
故选：B.
6．（2022·黑龙江哈尔滨·模拟预测）在中，角的对边分别为，若，，则面积的最大值为（ ）
A．B．C．D．
【答案】B
【分析】利用正弦定理边化角可化简已知等式求得，进而得到；利用余弦定理和基本不等式可求得，代入三角形面积公式即可求得结果.
【详解】由正弦定理得：，
，
，，，，，
，解得：；
由余弦定理得：，
（当且仅当时取等号），，
.
故选：B.
7．（2024·陕西·模拟预测）在中，角所对的边分别为，已知，则面积的最大值为（ ）
A．B．C．12D．15.
【答案】C
【分析】先利用正弦定理化边为角，可得出的关系，再利用余弦定理求出，进而可得出，再根据三角形的面积公式结合二次函数的性质即可得解.
【详解】由，由正弦定理得，即，
所以，
由余弦定理得，
所以，
所以，
当，即时，取得最大值.
故选：C.
8．（2024·全国·模拟预测）已知外接圆的半径为，为边的中点，，为钝角，则的取值范围是（ ）
A．B．C．D．
【答案】C
【分析】解法一：利用正弦定理和外接圆的半径可求得，设，利用正弦定理将，用角的三角函数表示出来，再利用三角恒等变换及三角函数的值域即可求解；
解法二：利用正弦定理和外接圆的半径可求得，利用向量可得，令，再由关于的方程至少有1个正根，利用判别式可得其范围；
解法三：利用正弦定理和外接圆的半径可求得，在和中，分别利用余弦定理可得，令，再由关于的方程至少有1个正根，利用判别式可得其范围.
【详解】解法一：
根据正弦定理得，所以，
因为为钝角，所以；
延长到，使得，连接，如下图所示：
易知四边形为平行四边形，且．
设，则，所以，
即，
所以，，
所以，
因为，所以，所以，
所以，
可得的取值范围是．
解法二：
根据正弦定理得，
所以，因为为钝角，所以
因为为边的中点，所以，可得，
设，则①．
设，则，
将其代入①得②，
所以关于的方程至少有1个正根；
当，即，
经检验，当时，方程②即，解得，则，不合题意；
当时，方程②即，解得，不符合题意；
所以或，解得，
故的取值范围是．
解法三：
根据正弦定理得，
所以，因为为钝角，所以；
设，根据余弦定理得，
在中易知，
又在中可得，
所以可得，即，
将代入，得①，
设，则，
将其代入①得②，
所以关于的方程至少有1个正根；
当，即，
经检验，当时，方程②即，解得，则，不合题意；
当时，方程②即，解得，不符合题意；
所以或，解得，
故的取值范围是．
故选：C
【点睛】解三角形中的最值或范围问题主要有两种解决方法：
一是将所求量表示为与边有关的形式，利用函数知识或基本不等式求得最值或范围；
二是将所求量用三角形的某一个角的三角函数表示，结合角的范围确定最值或范围．
二、多选题
9．（2024·甘肃兰州·一模）某学校开展测量旗杆高度的数学建模活动，学生需通过建立模型、实地测量，迭代优化完成此次活动．在以下不同小组设计的初步方案中，可计算出旗杆高度的方案有
A．在水平地面上任意寻找两点，，分别测量旗杆顶端的仰角，，再测量，两点间距离
B．在旗杆对面找到某建筑物（低于旗杆），测得建筑物的高度为，在该建筑物底部和顶部分别测得旗杆顶端的仰角和
C．在地面上任意寻找一点，测量旗杆顶端的仰角，再测量到旗杆底部的距离
D．在旗杆的正前方处测得旗杆顶端的仰角，正对旗杆前行5m到达处，再次测量旗杆顶端的仰角
【答案】BCD
【分析】根据各选项的描述，结合正余定理的边角关系判断所测数据是否可以确定旗杆高度即可.
【详解】对于A：如果，两点与旗杆底部不在一条直线上时，就不能测量出旗杆的高度，故A不正确．
对于B：如下图， 中由正弦定理求，则旗杆的高，故B正确；
对于C：在直角三角形直接利用锐角三角函数求出旗杆的高，故C正确；
对于D：如下图，中由正弦定理求，则旗杆的高，故D正确；
故选：BCD.
10．（2023·安徽亳州·模拟预测）已知三个内角、、的对应边分别为、、，且，.则下列结论正确的是（ ）
A．面积的最大值为
B．
C．的最大值为
D．的取值范围为
【答案】ACD
【分析】利用基本不等式、余弦定理可求得的最大值，结合三角形的面积公式可判断A选项；利用余弦定理可判断B选项；利用正弦定理、平面向量数量积的定义、三角恒等变换化简，结合正弦函数的基本性质可判断C选项；利用三角恒等变换可得出，结合正切函数的基本性质可判断D选项.
【详解】对于A选项，因为，，由余弦定理和基本不等式可得
，即，
当且仅当时，等号成立，
故，
所以，的面积的最大值为，A对；
对于B选项，，B错；
对于C选项，由正弦定理可得，则，
因为，则，所以，，
由平面向量数量积的定义可得
，
当且仅当时，即当时，等号成立，
故的最大值为，C对；
对于D选项，因为，则，
由题意可知，，所以，，
，
当时，，则；
当时，，则.
综上所述，的取值范围为，D对.
故选：ACD.
11．（2024·贵州黔南·二模）已知锐角的三个内角，，的对边分别是，，，且的面积为.则下列说法正确的是（ ）
A．
B．的取值范围为
C．若，则的外接圆的半径为2
D．若，则的面积的取值范围为
【答案】ABD
【分析】对A：借助面积公式与余弦定理计算即可得；对B：借助锐角三角形定义与三角形内角和计算即可得；对C：借助正弦定理计算即可得；对D：借助正弦定理，结合面积公式将面积用单一变量表示出来，结合的范围即可得解.
【详解】对A：由题意可得，由余弦定理可得，
即有，即，
由，故，即，故A正确；
对B：则，，解得，故B正确；
对C：由正弦定理可得，即，故C错误；
对D：若，则，
由正弦定理可得，即，
即
，
由，则，故，故D正确.
故选：ABD.
【点睛】关键点点睛：D选项关键点在于借助正弦定理，结合面积公式将面积用单一变量表示出来，结合的范围即可得解.
三、填空题
12．（2024·全国·模拟预测）已知在锐角三角形ABC中，角A，B，C所对的边分别是a，b，c，且，则的面积S的取值范围为 ．
【答案】
【分析】利用正弦定理解三角形，利用三角函数的单调性求三角形的面积的取值范围.
【详解】由题意及正弦定理，得．
因为，所以．
因为，所以，所以．
因为，所以，
由正弦定理，得，
所以，
因为是锐角三角形，所以解得，
所以，所以，从而．
13．（2024·上海金山·二模）某临海地区为保障游客安全修建了海上救生栈道，如图，线段、是救生栈道的一部分，其中，，在的北偏东方向，在的正北方向，在的北偏西方向，且．若救生艇在处载上遇险游客需要尽快抵达救生栈道，则最短距离为 m．(结果精确到1 m)
【答案】
【分析】先在中求出AC，再利用正弦定理，在中求出，进而转化到中求解即可.
【详解】解：作交于E，由题意可得如图：
，
所以，
，
在中，由正弦定理可得：
，
所以，
所以，
，
在直角中，，
故答案为：475.
14．（2024·福建莆田·二模）如图，点是边长为1的正六边形的中心，是过点的任一直线，将此正六边形沿着折叠至同一平面上，则折叠后所成图形的面积的最大值为 ．

【答案】
【分析】根据正六边形的性质和对称性，可将问题转化为求三角形面积最大值问题，结合基本不等式求出最值即可.
【详解】
如图，由对称性可知，折叠后的图形与另外一半不完全重合时比完全重合时面积大，
此时，折叠后面积为正六边形面积的与面积的3倍的和.
由正六边形的性质和对称性知，，，
在中，由余弦定理可得：
，
得，
由基本不等式可知，则，
故，
因，，解得，
当且仅当时等号成立，
故，
又正六边形的面积，
所以折叠后的面积最大值为：.
故答案为：.
【点睛】关键点点睛：本题解决的关键是，分析得折叠后所成图形的面积要取得最大值时的状态，从而得解.
四、解答题
15．（2024·福建漳州·模拟预测）如图，在四边形中，，，且的外接圆半径为4.
(1)若，，求的面积；
(2)若，求的最大值.
【答案】(1)4；
(2).
【分析】（1）在三角形中，根据正弦定理求得，再在三角形中，利用三角形面积公式即可求得结果；
（2）设，在三角形中分别用正弦定理表示，从而建立关于的三角函数，进而求三角函数的最大值，即可求得结果.
【详解】（1）因为，的外接圆半径为4，所以，解得.
在中，，则，解得.
又，所以；
在中，，，，
所以.
（2）设，.
又，所以.
因为，所以.
在中，，由正弦定理得，
即，解得
.
在中，，由正弦定理得，
即，解得，
所以.
又，所以，
当且仅当，即时，取得最大值1，
所以的最大值为.
16．（2023·湖北孝感·模拟预测）汾阳文峰塔建于明末清初，位于山西省汾阳市城区以东2公里的建昌村，该塔共十三层，雄伟挺拔，高度位于中国砖结构古塔之首.如图，某测绘小组为了测量汾阳文峰塔的实际高度AB，选取了与塔底B在同一水平面内的三个测量基点C，D，E，现测得，，，，，在点C测得塔顶A的仰角为.参考数据：取，，.

(1)求；
(2)求塔高（结果精确到1m）.
【答案】(1)
(2)85m
【分析】（1）在中，由余弦定理即可得解；
（2）在中，先利用正弦定理求出，再解即可.
【详解】（1）在中，由余弦定理得，
则
；
（2）在中，由正弦定理得，
则，
在中，，
所以，
故塔高为85m.
17．（2024·重庆·模拟预测）如图，某班级学生用皮尺和测角仪（测角仪的高度为1.7m）测量重庆瞰胜楼的高度，测角仪底部A和瞰胜楼楼底O在同一水平线上，从测角仪顶点C处测得楼顶M的仰角，（点E在线段MO上）．他沿线段AO向楼前进100m到达B点，此时从测角仪顶点D处测得楼顶M的仰角，楼尖MN的视角（N是楼尖底部，在线段MO上）．
(1)求楼高MO和楼尖MN；
(2)若测角仪底在线段AO上的F处时，测角仪顶G测得楼尖MN的视角最大，求此时测角仪底到楼底的距离FO．
参考数据：，，，
【答案】(1)，
(2)FO为37．4m
【分析】（1）法一：在中，由正弦定理得，可得，进而求得MO，进而求得CE，计算可求得楼离MO和楼尖MN；
法二：利用，，可求得ME，进而计算可求得楼离MO和楼尖MN；
（2）设，，，进而可得，利用基本不等式可求得楼尖MN的视角最大时x的值．
【详解】（1）法一：，，∴．
在中，由正弦定理得，，
又，∴．
∴，
∴．
（m）．
∴．
∵，∴，．
法二：，，
∴，
即，∴，
∴．
m．
∴．
∵，∴，．
（2）设，，，
∴
，
当且仅当，即时，等号成立．
∴测角仪底到楼底的距离FO为37．4m处时，测得楼尖MN的视角最大．
18．（2024·四川德阳·二模）的内角的对边分别为，已知.
(1)求；
(2)若为锐角三角形，且，求面积的取值范围.
【答案】(1)
(2)
【分析】（1）利用二倍角公式以及同角三角函数关系化简已知等式，可得，即可求得答案；
（2）利用正弦定理求出a的表达式，并结合恒等变换公式化简，利用为锐角三角形，求出角C的范围，即可求得a的取值范围，再利用三角形面积公式，即可求得答案.
【详解】（1）因为中，，即，
而，故，
故，又，
则；
（2）由（1）以及题设可得；
由正弦定理得
，
因为为锐角三角形，，，
则，
则，则，
即，则，
即面积的取值范围为.
19．（2024·全国·模拟预测）记锐角三角形的内角，，的对边分别为，，，已知，.
(1)求.
(2)求面积的取值范围.
【答案】(1)；
(2).
【分析】（1）方法一：由余弦定理角化边求解；方法二：由正弦定理边化角求解.
（2）利用正弦定理得，结合为锐角三角形，求得，进而求得，即可求解.
【详解】（1）方法一：由余弦定理，得，解得.
又，所以由正弦定理，得.
又为锐角三角形，所以.
方法二：由题意知，.
由正弦定理得，
所以，
所以，即；
又因为，所以，又因为，所以.
（2）由正弦定理，得；
因为为锐角三角形，所以，
解得，所以，所以.
因为，所以，所以.
故面积的取值范围为.
【拓展冲刺练】
一、单选题
1．（23-24高三上·安徽铜陵·阶段练习）镇国寺塔亦称西塔，是一座方形七层楼阁式砖塔，顶端塔刹为一青铜铸葫芦，葫芦表面刻有“风调雨顺､国泰民安”八个字，是全国重点文物保护单位､国家3A级旅游景区，小胡同学想知道镇国寺塔的高度MN，他在塔的正北方向找到一座建筑物AB，高为7.5，在地面上点C处（B，C，N在同一水平面上且三点共线）测得建筑物顶部A，镇国寺塔顶部M的仰角分别为15°和60°，在A处测得镇国寺塔顶部M的仰角为30°，则镇国寺塔的高度约为（ ）（参考数据：）

A．B．C．D．
【答案】C
【分析】由已知，在中应用正弦定理得，再由倍角余弦公式求，进而求镇国寺塔的高度.
【详解】在中，则，
所以，而，，
所以，又，
则.
故选：C
2．（2023·贵州·二模）镜面反射法是测量建筑物高度的重要方法，在如图所示的模型中．已知人眼距离地面高度，某建筑物高，将镜子（平面镜）置于平地上，人后退至从镜中能够看到建筑物的位置，测量人与镜子的距离，将镜子后移a米，重复前面中的操作，则测量人与镜子的距离，则镜子后移距离a为（ ）
A．6mB．5mC．4mD．3m
【答案】A
【分析】设建筑物底部到第一次观察时镜面位置之间的距离为，根据光线反射性质列出关于的方程组，求解即可.
【详解】
如图：设建筑物最高点为A，建筑物底部为，第一次观察时镜面位置为，第一次观察时人眼睛位置为C处，第二次观察时镜面位置为，
设到之间的距离为，
由光线反射性质得，所以，即，①
同理可得，②
①②两式相比得，解得，
代入①得，
故选：A．
3．（2023·广西柳州·模拟预测）在中，角、、所对的边分别为、、，已知，，则面积的最大值为（ ）
A．B．C．D．
【答案】B
【分析】利用余弦定理结合基本不等式可求得的最大值，再利用三角形的面积公式可求得面积的最大值.
【详解】由余弦定理可得，即，
当且仅当时，等号成立，故.
因此，面积的最大值为.
故选：B.
4．（2024·全国·模拟预测）已知是锐角三角形，内角A，B，C所对应的边分别为a，b，c．若，则的取值范围是（ ）
A．B．C．D．
【答案】C
【分析】由余弦定理和正弦定理，结合正弦和角公式得到，结合为锐角三角形，得到，故，再利用正弦定理得到，求出取值范围即可.
【详解】因为，得．
由余弦定理得，
所以，即．
由正弦定理得，
因为，则，
所以，即．
因为是锐角三角形，所以，，所以．
又在上单调递增，所以，则．
因为是锐角三角形，所以，，，
所以，
由正弦定理得
，
令，因为，所以．
在上单调递增，
当时，，当时，，
故
故选：C．
【点睛】解三角形中最值或范围问题，通常涉及与边长，周长有关的范围问题，与面积有关的范围问题，或与角度有关的范围问题，
常用处理思路：①余弦定理结合基本不等式构造不等关系求出答案；
②采用正弦定理边化角，利用三角函数的范围求出最值或范围，如果三角形为锐角三角形，或其他的限制，通常采用这种方法；
③巧妙利用三角换元，实现边化角，进而转化为正弦或余弦函数求出最值.
二、多选题
5．（2022·广东佛山·一模）在中，、、所对的边为、、，设边上的中点为，的面积为，其中，，下列选项正确的是（ ）
A．若，则B．的最大值为
C．D．角的最小值为
【答案】ABC
【分析】利用余弦定理结合三角形的面积公式可判断A选项的正误；利用基本不等式结合三角形的面积公式可判断B选项的正误；利用余弦定理可判断C选项的正误；利用余弦定理结合基本不等式可判断D选项的正误.
【详解】对于A，由余弦定理可得，得，
故，A对；
对于B，由基本不等式可得，即，
当且仅当时，等号成立，
由余弦定理可得，
则，B对；
对于C，，则，
由余弦定理可得，，
所以，，整理可得，
则，C对；
对于D，由余弦定理可得，
当且仅当时，等号成立，
因为且函数在上单调递减，故，D错.
故选：ABC.
6．（2022·河北沧州·模拟预测）在中，三边长分别为a，b，c，且，则下列结论正确的是（ ）
A．B．
C．D．
【答案】ABC
【分析】根据题意得，结合边的关系即可判断A；根据边的关系及基本不等式即可判断BC；用边长为的三角形的周长判断D
【详解】对于A，，即，也就是，
另一方面，在中，，则成立，故A正确；
对于B，，故B正确；
对于C，，当且仅当时取等号，故C正确；
对于D，边长为的三角形，满足，但，故D错误．
故选：ABC．
三、填空题
7．（2024·福建漳州·模拟预测）如图，某城市有一条公路从正西方向通过路口后转向西北方向，围绕道路打造了一个半径为的扇形景区，现要修一条与扇形景区相切的观光道，则的最小值为 ．
【答案】
【分析】在中，利用余弦定理结合基本不等式可得，利用正弦定理可得，利用三角函数的有界性建立不等式，即可求解.
【详解】如图，设切点为，连接．由题意得，
设，
在中，
,
当且仅当时取等号．
设，则，
所以，
故
（当且仅当时取等号），
所以，
解得，所以的最小值为．
故答案为：.
8．（2023·陕西西安·模拟预测）在平面四边形中，，则四边形的面积的最大值为 ．
【答案】6
【分析】在中，利用正弦定理可得，进而可求得的面积，在中，由余弦定理可得，进而可得的面积，即可得结果.
【详解】在中，由正弦定理，可得，
所以的面积；
在中，由余弦定理，
当且仅当时，等号成立，
即，且，则，
所以的面积；
显然当B、D位于直线AC的两侧时，四边形ABCD的面积较大，
此时四边形的面积.
所以四边形的面积的最大值为.
故答案为：6.
【点睛】方法点睛：与解三角形有关的交汇问题的关注点
（1）根据条件恰当选择正弦、余弦定理完成边角互化；
（2）结合三角恒等变换、三角函数以及基本不等式分析运算．
四、解答题
9．（2024·山西·一模）中角所对的边分别为，其面积为，且.
(1)求；
(2)已知，求的取值范围.
【答案】(1)
(2)
【分析】（1）根据面积公式以及余弦定理即可求解，进而可求解，
（2）根据余弦定理结合不等式即可求解.
【详解】（1）因为三角形的面积为，
则，
所以，又，则；
（2）由于，所以，
即，取等号，
故，
故
10．（2024·全国·模拟预测）在①；②两个条件中任选一个，补充在下面的问题中，并解答该问题．在中，内角所对的边分别是，且______．
(1)求角的大小；
(2)若点满足，且线段，求面积的最大值．
【答案】(1)
(2)
【分析】（1）①由三角恒等变换可得；②由正弦定理和正弦展开式可得；
（2）由余弦定理和基本不等式求出，再求出面积最值即可.
【详解】（1）选①，，
所以．
因为，所以，即，
所以．
选②．由及正弦定理得，
所以．
因为，，所以，
所以，
所以．
（2）如图，
点满足，则，故，又，
故，
即，即，当且仅当时，取等号，
故，即面积的最大值为．
11．（2023·四川达州·二模）在中，角、、所对的边分别为、、，.
(1)求；
(2)若，求面积的最小值.
【答案】(1)
(2)
【分析】（1）利用正弦定理结合两角和的余弦公式化简可得出，即可求得的值；
（2）分析可知、均为锐角，利用两角和的正切公式结合基本不等式可得出，求出的最小值，即可求得的最小值.
【详解】（1）解：，
.
由正弦定理得.
.
因为，则，
，，
则，
所以，，即，
所以，，
，即.
（2）解：由（1）得.
若，则、均为钝角，则，矛盾，
所以，，，此时、均为锐角，合乎题意，
，
当且仅当时，等号成立，且为钝角.
，则，且为锐角，
由，解得，即，
当且仅当时，等号成立，
，.
因此，面积的最小值为
术语名称
术语意义
图形表示
仰角与俯角
在目标视线与水平视线(两者在同一铅垂平面内)所成的角中，目标视线在水平视线上方的叫做仰角，目标视线在水平视线下方的叫做俯角
方位角
从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角．方位角θ的范围是0°≤θ