2025年新高考数学精析考点考点49直线与圆、圆与圆的位置关系(3种核心题型+基础保分练+综合提升练+拓展冲刺练)(原卷版+解析)

这是一份2025年新高考数学精析考点考点49直线与圆、圆与圆的位置关系(3种核心题型+基础保分练+综合提升练+拓展冲刺练)(原卷版+解析)，文件包含2025年新高考数学精析考点考点49直线与圆圆与圆的位置关系3种核心题型+基础保分练+综合提升练+拓展冲刺练原卷版docx、2025年新高考数学精析考点考点49直线与圆圆与圆的位置关系3种核心题型+基础保分练+综合提升练+拓展冲刺练解析版docx等2份试卷配套教学资源，其中试卷共73页， 欢迎下载使用。
【考试提醒】
1.能根据给定直线、圆的方程，判断直线与圆、圆与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题．
【知识点】
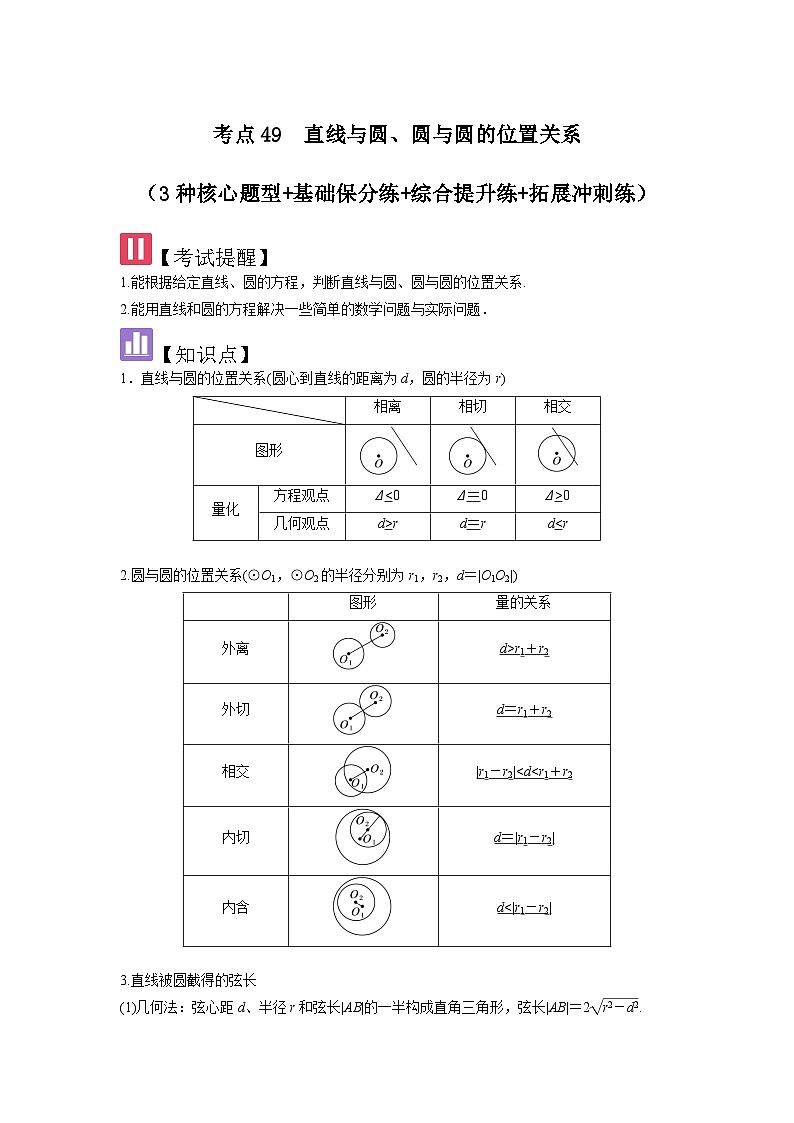
1．直线与圆的位置关系(圆心到直线的距离为d，圆的半径为r)
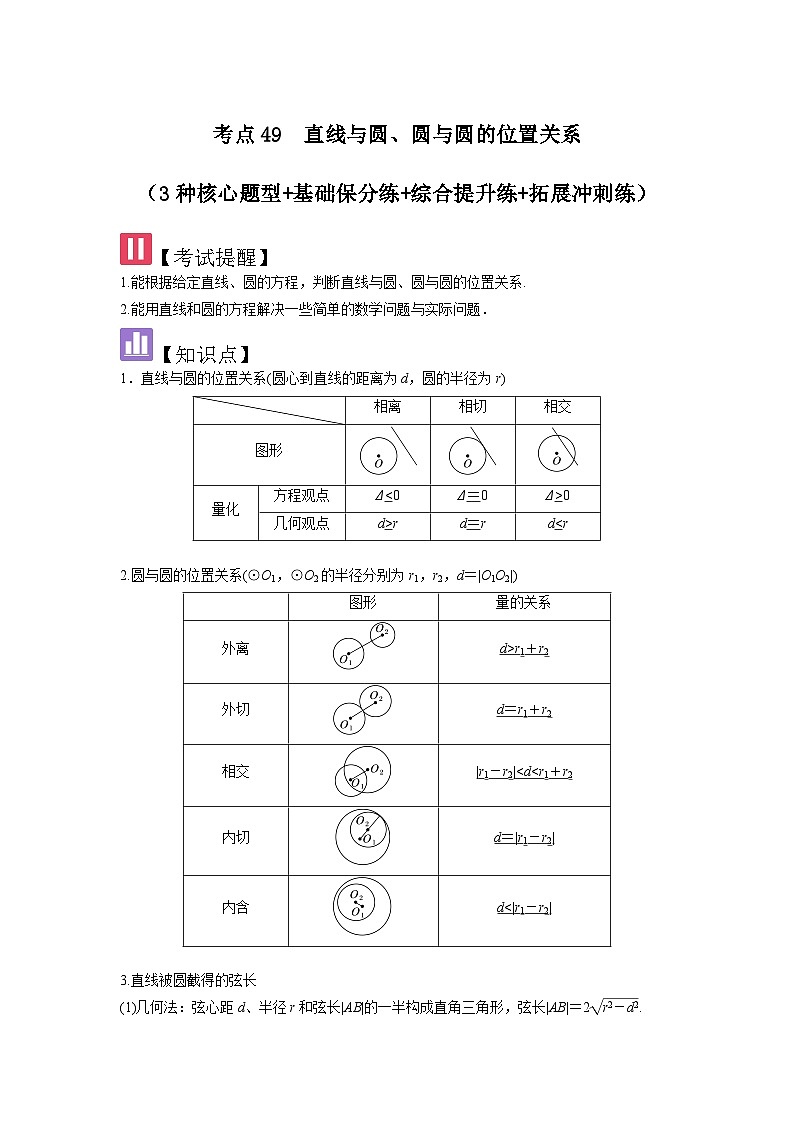
2.圆与圆的位置关系(⊙O1，⊙O2的半径分别为r1，r2，d＝|O1O2|)
3.直线被圆截得的弦长
(1)几何法：弦心距d、半径r和弦长|AB|的一半构成直角三角形，弦长|AB|＝2eq \r(r2－d2).
(2)代数法：设直线y＝kx＋m与圆x2＋y2＋Dx＋Ey＋F＝0相交于点M，N，代入，消去y，得关于x的一元二次方程，则|MN|＝eq \r(1＋k2)·eq \r(xM＋xN2－4xMxN).
常用结论
1．圆的切线方程常用结论
(1)过圆x2＋y2＝r2上一点P(x0，y0)的圆的切线方程为x0x＋y0y＝r2.
(2)过圆x2＋y2＝r2外一点M(x0，y0)作圆的两条切线，则两切点所在直线方程为x0x＋y0y＝r2.
2．圆与圆的位置关系的常用结论
(1)两圆相交时，其公共弦所在的直线方程由两圆方程相减得到．
(2)两个圆系方程
①过直线Ax＋By＋C＝0与圆x2＋y2＋Dx＋Ey＋F＝0交点的圆系方程为x2＋y2＋Dx＋Ey＋F＋λ(Ax＋By＋C)＝0(λ∈R)；
②过圆C1：x2＋y2＋D1x＋E1y＋F1＝0和圆C2：x2＋y2＋D2x＋E2y＋F2＝0交点的圆系方程为x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2)＝0(λ≠－1)(其中不含圆C2，所以注意检验C2是否满足题意，以防丢解)
【核心题型】
题型一 直线与圆的位置关系
命题点1 位置关系的判断
判断直线与圆的位置关系的常见方法
(1)几何法：利用d与r的关系判断．
(2)代数法：联立方程之后利用Δ判断．
(3)点与圆的位置关系法：若直线恒过定点且定点在圆内，可判断直线与圆相交．
【例题1】（2024·安徽·模拟预测）已知直线，圆，则该动直线与圆的位置关系是（ ）
A．相离B．相切C．相交D．不确定
【变式1】（2024·全国·模拟预测）已知D，E为正实数，则直线与圆的位置关系是（ ）
A．相离B．相切C．相交且不过圆心D．相交且过圆心
【变式2】（2024·山西临汾·一模）已知点在圆内，则直线与圆的位置关系是 .
【变式3】（2022·江苏南京·模拟预测）已知动点是曲线上任一点，动点到点的距离和到直线的距离相等，圆的方程为．
(1)求的方程，并说明是什么曲线；
(2)设、、是上的三个点，直线、均与圆相切，判断直线与圆的位置关系，并说明理由．
命题点2 弦长问题
弦长的两种求法
(1)代数法：将直线和圆的方程联立方程组，根据弦长公式求弦长．
(2)几何法：若弦心距为d，圆的半径长为r，则弦长l＝2eq \r(r2－d2).
【例题2】（2024·江苏扬州·模拟预测）圆被直线所截线段的长度为（ ）
A．2B．4C．D．
【变式1】（2024·贵州六盘水·三模）已知直线与圆相交于A，B两点，若，则（ ）
A．B．1C．D．﹣2
【变式2】（2024·四川自贡·三模）已知圆的圆心是抛物线的焦点，直线与圆相交于，两点，，则圆的半径为 ．
【变式3】（2023·陕西咸阳·三模）直线（t为参数），圆（极轴与x轴的非负半轴重合，且单位长度相同）．
(1)求圆心C到直线l的距离；
(2)若直线l被圆C截得的弦长为，求a的值．
命题点3 切线问题
当切线方程斜率存在时，圆的切线方程的求法
(1)几何法：设切线方程为y－y0＝k(x－x0)，利用点到直线的距离公式表示出圆心到切线的距离d，然后令d＝r，进而求出k.
(2)代数法：设切线方程为y－y0＝k(x－x0)，与圆的方程组成方程组，消元后得到一个一元二次方程，然后令判别式Δ＝0进而求得k.
注意验证斜率不存在的情况
【例题3】（2024·山东菏泽·模拟预测）过点向圆作两条切线，切点分别为，若，则（ ）
A．或B．或C．或D．或
【变式1】（2024·浙江·模拟预测）过点作圆：的两条切线，切点分别为，，则原点到直线的距离为（ ）
A．B．C．D．
【变式2】（2024·江苏扬州·模拟预测）已知圆C与两坐标轴及直线都相切，且圆心在第二象限，则圆C的方程为 ．
【变式3】（2023高三上·全国·专题练习）已知点,直线及圆．
(1)若直线与圆相切,求的值．
(2)求过点的圆的切线方程．
命题点4 直线与圆位置关系中的最值(范围)问题
涉及与圆的切线有关的线段长度范围(最值)问题，解题关键是能够把所求线段长度表示为关于圆心与直线上的点的距离的函数的形式，利用求函数值域的方法求得结果．
【例题4】（23-24高三下·广东深圳·期中）已知直线与圆相交于两点，则当取最小值时，实数的值为（ ）
A．2B．1C．-1D．-2
【变式1】（2024·湖北·模拟预测）在平面直角坐标系中，已知圆，若正三角形的一边为圆的一条弦，则的最大值为（ ）
A．1B．C．D．2
【变式2】（2024·四川泸州·三模）动直线l：被圆C：截得弦长的最小值为 ．
【变式3】（2024·河南·三模）在平面直角坐标系中，已知点，点（不位于轴左侧）到轴的距离为．
(1)求点的轨迹方程；
(2)若圆与点的轨迹有且仅有一个公共点，求的最大值；
(3)在（2）的条件下，当取最大值，且时，过作圆的两条切线，分别交轴于两点，求面积的最小值．
题型二 圆与圆的位置关系
(1)判断两圆的位置关系时常用几何法，即利用两圆圆心之间的距离与两圆半径之间的关系，一般不采用代数法．
(2)若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差消去x2，y2项得到
【例题5】（2024·山东·模拟预测）已知圆的圆心到直线的距离是，则圆与圆的位置关系是（ ）
A．相离B．相交C．内切D．内含
【变式1】（2024·吉林长春·模拟预测）已知圆，圆，则这两圆的位置关系为（ ）
A．内含B．相切C．相交D．外离
【变式2】（2024·新疆喀什·二模）已知圆和圆，则两圆公共弦所在直线的方程为 ．
【变式3】（2023·全国·模拟预测）在平面直角坐标系中，圆．以坐标原点为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方程为．
(1)判断圆与圆的位置关系；
(2)若直线的极坐标方程为，直线与轴交于点，与圆交于两点，求的值．
【课后强化】
【基础保分练】
一、单选题
1．（2024·河北石家庄·三模）已知圆和圆，则两圆公切线的条数为（ ）
A．1B．2C．3D．4
2．（2024·安徽·三模）直线：与圆：的公共点的个数为（ ）
A．0B．1C．2D．1或2
3．（2024·陕西铜川·模拟预测）已知，，若圆上存在点P满足，则a的取值范围是（ ）
A．B．C．D．
4．（2024·北京·三模）已知直线，圆，下列说法错误的是（ ）
A．对任意实数，直线与圆有两个不同的公共点；
B．当且仅当时，直线被圆所截弦长为；
C．对任意实数，圆不关于直线对称；
D．存在实数，使得直线与圆相切．
二、多选题
5．（2024·广东茂名·一模）已知圆，则（ ）
A．圆的圆心坐标为
B．圆的周长为
C．圆与圆外切
D．圆截轴所得的弦长为3
6．（2024·福建南平·二模）已知圆：，直线：，则（ ）
A．直线过定点
B．圆被轴截得的弦长为
C．当时，圆上恰有2个点到直线距离等于4
D．直线被圆截得的弦长最短时，的方程为
三、填空题
7．（2024·天津武清·模拟预测）已知直线与圆C：相交于A，B两点，且，则实数 .
8．（2024·河北邢台·一模）已知，过点恰好只有一条直线与圆E：相切，则 ，该直线的方程为 ．
9．（2024·广东汕头·三模）已知圆经过，，三点，
（i）则圆的标准方程为 ；
（ii）若直线关于对称的直线与圆有公共点，则的取值范围是 .
四、解答题
10．（2024·全国·模拟预测）已知点在抛物线上，点是抛物线上的两个动点，直线与的倾斜角互补．
(1)求抛物线的方程和直线的斜率；
(2)设的外接圆为圆，过点作抛物线的切线，证明：直线与圆相切．
11．（2024·山西晋中·模拟预测）已知椭圆 过点，且离心率为.
(1)求椭圆的方程；
(2)已知圆方程为，过圆上任意一点作圆的切线，切线与椭圆交于，两点，为坐标原点，设为的中点，当取最大值时，求直线的方程.
【综合提升练】
一、单选题
1．（2024·四川成都·一模）圆：与直线：的位置关系为（ ）
A．相切B．相交C．相离D．无法确定
2．（2024·河南·模拟预测）直线被圆截得的弦长为（ ）
A．B．C．D．
3．（2024·河南·模拟预测）直线，圆.则直线被圆所截得的弦长为（ ）
A．2B．C．D．
4．（2024·江西·模拟预测）已知实数满足，则的最小值为（ ）
A．B．2C．D．4
5．（2024·全国·模拟预测）已知圆，直线都经过原点，且，若与被圆所截得的弦长之比为，则直线的斜率为（ ）
A．B．C．D．
6．（2024·陕西安康·模拟预测）已知直线与圆相交于两点，若的面积为50，则的值为（ ）
A．或B．或
C．或D．或
7．（2024·辽宁·模拟预测）过点作圆的切线，为切点，，则的最大值是（ ）
A．B．C．D．
8．（2023·陕西榆林·模拟预测）已知直线与圆相切，交曲线于点，若是坐标原点，则以为圆心，以为半径的圆与圆的位置关系为（ ）
A．相交B．内含C．外离D．外切
二、多选题
9．（2023·全国·模拟预测）在平面直角坐标系中，，，点满足，记动点的轨迹为曲线，直线：，，则下列结论中正确的是（ ）
A．曲线的周长为
B．直线与曲线的位置关系无法确定
C．的最大值为3
D．若直线与曲线相交，其弦长为4，则
10．（2023·福建·模拟预测）已知，，则下列说法正确的是（ ）
A．若，两圆的公切线过点
B．若，两圆的相交弦长为
C．若两圆的一个交点为，分别过点的两圆的切线相互垂直，则
D．若时，两圆的位置关系为内含
11．（2024·山西晋中·模拟预测）已知圆，直线是直线上的动点，过点作圆的切线，切点为，则当切线长取最小值时，下列结论正确的是（ ）
A．B．点的坐标为
C．的方程可以是D．的方程可以是
三、填空题
12．（2022·上海·模拟预测）已知圆，则直线和圆的位置关系为 .
13．（2024·四川绵阳·模拟预测）直线，与圆相交于、两点，点为直线上一动点，则的最小值是 .
14．（2023·安徽马鞍山·模拟预测）在平面直角坐标系中，已知点，，若直线：上存在点使得，实数的取值范围是 .
四、解答题
15．（2024·全国·模拟预测）已知在平面直角坐标系xOy中，曲线的参数方程为（为参数），以坐标原点为极点，轴的非负半轴为极轴，建立极坐标系，直线的极坐标方程为，且直线与曲线交于A，B两点.
(1)求曲线C的极坐标方程以及直线的一般方程；
(2)若，求的值以及曲线上的点到直线距离的最大值．
16．（2024·四川南充·二模）已知点是抛物线上的定点，点是上的动点，直线的斜率分别为，且，直线是曲线在点处的切线.
(1)若，求直线的斜率；
(2)设的外接圆为，试判断直线与圆的位置关系，并说明理由.
17．（2024·陕西安康·模拟预测）已知抛物线的准线方程为，直线l与C交于A，B两点，且（其中O为坐标原点），过点O作交AB于点D.
(1)求点D的轨迹E的方程；
(2)过C上一点作曲线E的两条切线分别交y轴于点M，N，求面积的最小值.
18．（2024·福建福州·模拟预测）已知双曲线的上、下顶点分别为．
(1)若直线与交于两点，记直线与的斜率分别为，求的值；
(2)过上一点作抛物线的切线和，切点分别为，证明：直线与圆相切．
19．（2024·福建南平·模拟预测）已知抛物线的准线与圆相切．
(1)求的方程；
(2)点是上的动点，且，过点作圆的两条切线分别与交于两点，求面积的最小值．
【拓展冲刺练】
一、单选题
1．（2023·北京东城·二模）已知点在圆上，过作圆的切线，则的倾斜角为 （ ）
A．B．C．D．
2．（2024·江西宜春·模拟预测）圆与圆的公共弦长为（ ）
A．B．C．D．
3．（2024·四川攀枝花·三模）由直线上的一点向圆引切线，切点为，则的最小值为（ ）
A．B．2C．D．
4．（2023·山东青岛·三模）已知向量，，满足，，，则的最小值为（ ）
A．－1B．C．2D．1
二、多选题
5．（2023·河北沧州·模拟预测）已知点在直线上移动，圆，直线，是圆的切线，切点为，.设，则（ ）
A．存在点，使得
B．存在点，使得
C．当的坐标为时，的方程为
D．点的轨迹长度是
6．（2023·山东聊城·二模）设直线l与抛物线相交于A，B两点，与圆相切于点，且M为的中点．（ ）
A．当时，的斜率为2B．当时，
C．当时，符合条件的直线l有两条D．当时，符合条件的直线l有四条
三、填空题
7．（2024·陕西·模拟预测）圆上总存在两个点到的距离为1，则a的取值范围是 .
8．（2022·湖北十堰·三模）当圆的面积最小时，圆C与圆的位置关系是 .
9．（2023·全国·模拟预测）已知圆的圆心在直线上，点与都在圆上，圆，则与的位置关系是 .
四、解答题
10．（2023·四川遂宁·模拟预测）如图，已知椭圆的方程为，，，，点是椭圆上任一点，是以为直径的圆．
(1)当的面积为时，求所在直线的方程；
(2)当与直线相切时，求的方程；
(3)求证：总与某个定圆相切．
11．（23-24高三上·重庆·期末）已知，B，C是抛物线E：上的三点，且直线与直线的斜率之和为0．
(1)求直线的斜率；
(2)若直线，均与圆M：（）相切，且直线被圆M截得的线段长为，求r的值．
12．（2024·山西朔州·一模）已知抛物线的准线方程为，直线与圆相切于点，且圆心在直线上．
(1)求抛物线和圆的标准方程；
(2)若是轴上的两点，是抛物线上的动点，且直线与圆均相切，，求的周长最小时，点的坐标．
相离
相切
相交
图形
量化
方程观点
Δ0
几何观点
d>r
d＝r
dr1＋r2
外切
d＝r1＋r2
相交
|r1－r2|