新高考数学一轮复习核心考点讲练13空间向量与立体几何（36种题型10个易错考点）（2份，原卷版+解析版）

这是一份新高考数学一轮复习核心考点讲练13空间向量与立体几何（36种题型10个易错考点）（2份，原卷版+解析版），文件包含新高考数学一轮复习核心考点讲练13空间向量与立体几何36种题型10个易错考点原卷版doc、新高考数学一轮复习核心考点讲练13空间向量与立体几何36种题型10个易错考点解析版doc等2份试卷配套教学资源，其中试卷共153页， 欢迎下载使用。
本章内容是高考必考内容之一，多考查空间几何体的表面积与体积，空间中有关平行与垂直的判定，空间角与距离的求解，空间向量的应用等问题。
高考对本章内容的考查比较稳定，针对这一特点，复习时，首先梳理本章重要定理、公式与常用结论，扫清基础知识和公式障碍；然后分题型重点复习，重视向量法求解空间角、距离问题的思路与解题过程
三、 2023真题抢先刷，考向提前知
一．棱柱、棱锥、棱台的体积（共4小题）
1．（2023•新高考Ⅱ）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为 ．
2．（2023•新高考Ⅰ）在正四棱台ABCD﹣A1B1C1D1中，AB＝2，A1B1＝1，AA1＝，则该棱台的体积为 ．
3．（2023•天津）在三棱锥P﹣ABC中，线段PC上的点M满足PM＝PC，线段PB上的点N满足PN＝PB，则三棱锥P﹣AMN和三棱锥P﹣ABC的体积之比为（ ）
A．B．C．D．
（多选）4．（2023•新高考Ⅰ）下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（ ）
A．直径为0.99m的球体
B．所有棱长均为1.4m的四面体
C．底面直径为0.01m，高为1.8m的圆柱体
D．底面直径为1.2m，高为0.01m的圆柱体
二．二面角的平面角及求法（共6小题）
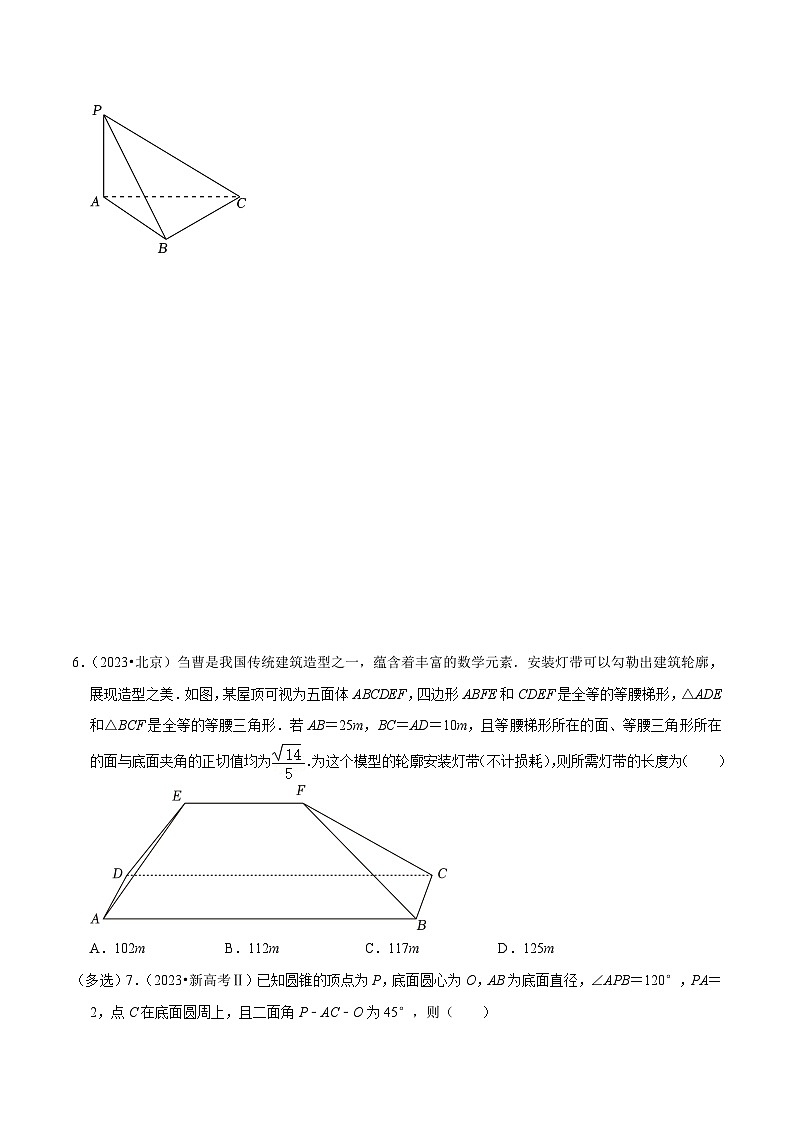
5．（2023•北京）如图，四面体P﹣ABC中，PA＝AB＝BC＝1，PC＝，PA⊥平面ABC．
（Ⅰ）求证：BC⊥平面PAB；
（Ⅱ）求二面角A﹣PC﹣B的大小．
6．（2023•北京）刍曹是我国传统建筑造型之一，蕴含着丰富的数学元素．安装灯带可以勾勒出建筑轮廓，展现造型之美．如图，某屋顶可视为五面体ABCDEF，四边形ABFE和CDEF是全等的等腰梯形，△ADE和△BCF是全等的等腰三角形．若AB＝25m，BC＝AD＝10m，且等腰梯形所在的面、等腰三角形所在的面与底面夹角的正切值均为．为这个模型的轮廓安装灯带（不计损耗），则所需灯带的长度为（ ）
A．102mB．112mC．117mD．125m
（多选）7．（2023•新高考Ⅱ）已知圆锥的顶点为P，底面圆心为O，AB为底面直径，∠APB＝120°，PA＝2，点C在底面圆周上，且二面角P﹣AC﹣O为45°，则（ ）
A．该圆锥的体积为πB．该圆锥的侧面积为4π
C．AC＝2D．△PAC的面积为
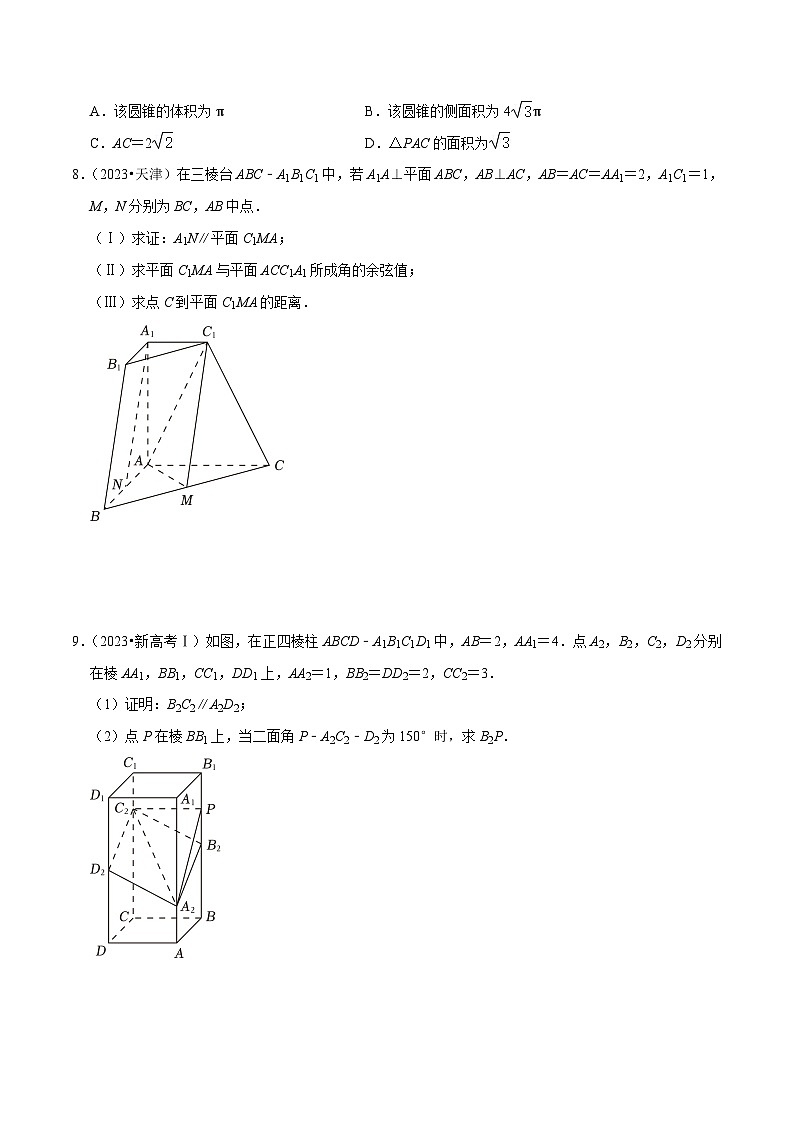
8．（2023•天津）在三棱台ABC﹣A1B1C1中，若A1A⊥平面ABC，AB⊥AC，AB＝AC＝AA1＝2，A1C1＝1，M，N分别为BC，AB中点．
（Ⅰ）求证：A1N∥平面C1MA；
（Ⅱ）求平面C1MA与平面ACC1A1所成角的余弦值；
（Ⅲ）求点C到平面C1MA的距离．
9．（2023•新高考Ⅰ）如图，在正四棱柱ABCD﹣A1B1C1D1中，AB＝2，AA1＝4．点A2，B2，C2，D2分别在棱AA1，BB1，CC1，DD1上，AA2＝1，BB2＝DD2＝2，CC2＝3．
（1）证明：B2C2∥A2D2；
（2）点P在棱BB1上，当二面角P﹣A2C2﹣D2为150°时，求B2P．
10．（2023•新高考Ⅱ）如图，三棱锥A﹣BCD中，DA＝DB＝DC，BD⊥CD，∠ADB＝∠ADC＝60°，E为BC中点．
（1）证明BC⊥DA；
（2）点F满足，求二面角D﹣AB﹣F的正弦值．
四、考点清单
1．特殊的四棱柱
2．球的截面的性质
(1)球的任何截面是圆面；
(2)球心和截面(不过球心)圆心的连线垂直于截面；
(3)球心到截面的距离d与球的半径R及截面的半径r的关系为r＝eq \r(R2－d2).
3．按照斜二测画法得到的平面图形的直观图，其面积与原图形面积的关系如下：
S直观图＝eq \f(\r(2),4)S原图形，S原图形＝2eq \r(2)S直观图．
4．正四面体的表面积与体积
棱长为a的正四面体，其表面积为eq \r(3)a2，体积为eq \f(\r(2),12)a3.
5．几个与球有关的切、接常用结论
(1)正方体的棱长为a，球的半径为R，
①若球为正方体的外接球，则2R＝eq \r(3)a；
②若球为正方体的内切球，则2R＝a；
③若球与正方体的各棱相切，则2R＝eq \r(2)a.
(2)若长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝eq \r(a2＋b2＋c2).
(3)正四面体的外接球与内切球的半径之比为3∶1，棱长为a的正四面体，其内切球半径R内＝eq \f(\r(6),12)a，外接球半径R外＝eq \f(\r(6),4)a.
6．异面直线的判定定理
经过平面内一点的直线与平面内不经过该点的直线互为异面直线．
7．等角定理的引申
(1)在等角定理中，若两角的两边平行且方向相同或相反，则这两个角相等．
(2)在等角定理中，若两角的两边平行且方向一个边相同，一个边相反，则这两个角互补．
8．唯一性定理
(1)过直线外一点有且只有一条直线与已知直线平行．
(2)过直线外一点有且只有一个平面与已知直线垂直．
(3)过平面外一点有且只有一个平面与已知平面平行．
(4)过平面外一点有且只有一条直线与已知平面垂直．
9.线、面平行的性质
(1)两个平面平行，其中一个平面内的任意一条直线平行于另一个平面．
(2)夹在两个平行平面间的平行线段长度相等．
(3)经过平面外一点有且只有一个平面与已知平面平行．
(4)两条直线被三个平行平面所截，截得的对应线段成比例．
(5)如果两个平面分别和第三个平面平行，那么这两个平面互相平行．
(6)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线，那么这两个平面平行．
(7)垂直于同一条直线的两个平面平行．
(8)垂直于同一平面的两条直线平行．
10．若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．
11．一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直．
12．两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．
13．过一点有且只有一条直线与已知平面垂直．
14．过一点有且只有一个平面与已知直线垂直．
15．空间向量加法、减法运算的两个技巧
(1)巧用相反向量：向量减法的三角形法则是解决空间向量加法、减法的关键，灵活运用相反向量可使向量首尾相接．
(2)巧用平移：利用三角形法则和平行四边形法则进行向量加、减法运算时，务必注意和向量、差向量的方向，必要时可采用空间向量的自由平移获得运算结果．
16．利用数乘运算进行向量表示的技巧
(1)数形结合：利用数乘运算解题时，要结合具体图形，利用三角形法则、平行四边形法则，将目标向量转化为已知向量．
(2)明确目标：在化简过程中要有目标意识，巧妙运用中点性质．
17.在几何体中求空间向量的数量积的步骤
1首先将各向量分解成已知模和夹角的向量的组合形式.
2利用向量的运算律将数量积展开，转化成已知模和夹角的向量的数量积.
3根据向量的方向，正确求出向量的夹角及向量的模.
4代入公式a·b＝|a||b|cs〈a，b〉求解.
18.利用空间向量证明或求解立体几何问题时，首先要选择基底或建立空间直角坐标系转化为其坐标运算，再借助于向量的有关性质求解(证).
19.求点到平面的距离的四步骤
20.用坐标法求异面直线所成角的一般步骤
(1)建立空间直角坐标系；
(2)分别求出两条异面直线的方向向量的坐标；
(3)利用向量的夹角公式计算两条直线的方向向量的夹角；
(4)结合异面直线所成角的范围求出异面直线所成的角．
21.利用向量法求两平面夹角的步骤
(1)建立空间直角坐标系；
(2)分别求出二面角的两个半平面所在平面的法向量；
(3)求两个法向量的夹角；
(4)法向量夹角或其补角就是两平面的夹角(不大于90°的角)
五、题型方法
一．构成空间几何体的基本元素（共1小题）
1．（2023•淮北一模）如图所示，在三棱台A′B′C′﹣ABC中，沿A′BC截去三棱锥A′﹣ABC，则剩余的部分是（ ）
A．三棱锥B．四棱锥C．三棱柱D．组合体
二．棱柱的结构特征（共1小题）
（多选）2．（2023•安徽模拟）如图，在直四棱柱ABCD﹣A1B1C1D1中，AB∥CD，AB＝2AD＝2DC＝2CB＝4，E，F，G分别为侧棱BB1，DD1，AA1上一点，BE＝DF＝A1G＝2，则（ ）
A．BD⊥GF
B．
C．∠EGF的最大值为
D．当 时，GE//C1F
三．棱锥的结构特征（共1小题）
3．（2023•天津一模）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥侧面积的一半，那么其侧面三角形底边上的高与底面正方形的边长的比值为（ ）
A．B．C．D．
四．棱台的结构特征（共1小题）
4．（2023•柳南区二模）如图，ABC﹣A1B1C1是一个正三棱台，而且下底面边长为6，上底面边长和侧棱长都为3，则棱台的高为（ ）
A．B．C．D．
五．旋转体（圆柱、圆锥、圆台）（共2小题）
5．（2023•南关区校级模拟）现有一个轴截面是边长为4的等边三角形的倒置圆锥（顶点在下方，底面在上方），将半径为的小球放入圆锥，使得小球与圆锥的侧面相切，过所有切点所在平面将圆锥分割成两个部分，则分割得到的圆台的侧面积为（ ）
A．B．C．D．
6．（2023•潍坊一模）在半径为1的球中作一个圆柱，当圆柱的体积最大时，圆柱的母线长为 ．
六．球内接多面体（共2小题）
7．（2023•山西模拟）在正三棱柱ABC﹣A1B1C1中，AB＝2，AA1＝3，以C1为球心，为半径的球面与侧面ABB1A1的交线长为（ ）
A．B．C．D．
8．（2023•江西模拟）若球O是正三棱锥A﹣BCD的外接球，，点E在线段BA上，BA＝3BE，过点E作球O的截面，则所得的截面中面积最小的截面的面积为（ ）
A．B．2πC．D．π
七．球外切几何体（共2小题）
9．（2023•全国模拟）四个半径为1的球两两相切，则它们的外切四面体棱长为（ ）
A．B．C．D．
（多选）10．（2023•小店区校级模拟）如图，棱长为2的正方体ABCD−A1B1C1D1的内切球球心为O，E、F分别是棱AB、CC1的中点，G在棱BC上移动，则（ ）
A．对于任意点G，OA∥平面EFG
B．存在点G，使OD⊥平面EFG
C．直线EF的被球O截得的弦长为
D．过直线EF的平面截球O所得截面圆面积的最小值为
八．棱柱、棱锥、棱台的侧面积和表面积（共2小题）
11．（2023•深圳模拟）圆锥侧面展开图扇形的圆心角为60°，底面圆的半径为8，则圆锥的侧面积为（ ）
A．384πB．392πC．398πD．404π
12．（2023•漳州模拟）已知某圆锥的底面半径为1，高为，则它的侧面积与底面积之比为（ ）
A．B．1C．2D．4
九．棱柱、棱锥、棱台的体积（共2小题）
13．（2023•贵阳模拟）已知球O的表面积为9π，若球O与正四面体S﹣ABC的六条棱均相切，则此四面体的体积为（ ）
A．9B．C．D．
14．（2023•保定二模）如图，在四面体ABCD中，AD⊥BC，BC＝2，AD＝4，AB+BD＝AC+CD＝6，则四面体ABCD体积的最大值为 ．
​
一十．球的体积和表面积（共2小题）
15．（2023•贵阳模拟）已知一圆锥内接于球，圆锥的表面积是其底面面积的3倍，则圆锥与球的体积之比是（ ）
A．B．C．D．
16．（2023•南江县校级模拟）在三棱锥P﹣ABC中，PA⊥平面ABC，AB＝AC，∠BAC＝90°，且AB+PA＝6，当三棱锥P﹣ABC的体积取最大值时，该三棱锥外接球的体积是（ ）
A．27πB．36πC．54πD．72π
一十一．多面体和旋转体表面上的最短距离问题（共1小题）
17．（2023•南宁模拟）如图，已知圆锥的底面半径为1，母线长SA＝3，一只蚂蚁从A点出发绕着圆锥的侧面爬行一圈回到点A，则蚂蚁爬行的最短距离为（ ）
A．6B．2πC．D．
一十二．三角形五心（共1小题）
18．（2023•河南模拟）已知点O为△ABC所在平面内一点，在△ABC中，满足，，则点O为该三角形的（ ）
A．内心B．外心C．垂心D．重心
一十三．组合几何体的面积、体积问题（共1小题）
19．（2023•东湖区校级一模）在多面体ABCDE中，平面ACDE⊥平面ABC，四边形ACDE为直角梯形，CD∥AE，AC⊥AE，AB⊥BC，CD＝1，AE＝AC＝2，F为DE的中点，且点G满足．
（1）证明：GF∥平面ABC；
（2）求多面体ABCDE的体积最大值．
一十四．平面图形的直观图（共1小题）
20．（2023•弥勒市校级模拟）如图，若斜边长为2的等腰直角△A'B'C'（B'与O'重合）是水平放置的△ABC的直观图，则△ABC的面积为（ ）
A．2B．2C．4D．8
一十五．斜二测法画直观图（共1小题）
21．（2023•建水县校级模拟）水平放置的平行四边形OABC，用斜二测画法画出它的直观图O'A'B'C'，如图所示．此直观图恰好是个边长为的正方形，则原平行四边形OABC的面积为 ．
一十六．平面的基本性质及推论（共1小题）
22．（2023•吉林模拟）已知α，β是两个不同的平面，则下列命题错误的是（ ）
A．若α∩β＝l，A∈α且A∈β，则A∈l
B．若A，B，C是平面α内不共线三点，A∈β，B∈β，则C∉β
C．若直线a⊂α，直线b⊂β，则a与b为异面直线
D．若A∈α且B∈α，则直线AB⊂α
一十七．异面直线及其所成的角（共2小题）
23．（2023•乌鲁木齐模拟）已知四棱柱ABCD﹣A1B1C1D1的底面是边长为2的正方形，侧棱与底面垂直，O为AC的中点，若点O到平面AB1D1的距离为，则直线OD1与直线BC1所成角的余弦值为 （ ）
A．B．C．D．
24．（2023•梅河口市校级一模）直三棱柱ABC﹣A1B1C1如图所示，AB＝4，BC＝3，AC＝5，D为棱AB的中点，三棱柱的各顶点在同一球面上，且球的表面积为61π，则异面直线A1D和B1C所成的角的余弦值为（ ）
A．B．C．D．
一十八．异面直线的判定（共2小题）
（多选）25．（2023•南通模拟）在三棱柱ABC﹣A1B1C1中，AB＝AC，B1C＝BC1，D是BC中点，则（ ）
A．直线AC1与A1D异面B．直线AD∥平面A1BC1
C．直线AA1⊥平面ABCD．直线BC⊥平面A1AD
（多选）26．（2023•西山区校级模拟）已知正方体ABCD﹣A1B1C1D1中，M为DD1的中点，则下列直线中与直线BM是异面直线的有（ ）
A．AA1B．BB1C．CC1D．DD1
一十九．空间中直线与直线之间的位置关系（共2小题）
27．（2023•新余二模）在长方体ABCD﹣A1B1C1D1中，AB＝AA1＝2，AD＝3，点E、F分别是棱AB、AA1的中点，E、F、C1∈平面α，直线A1D1∩平面α＝P，则直线BP与直线CD1所成角的余弦值为（ ）
A．B．C．D．
28．（2023•黄浦区校级三模）如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则（ ）
A．BM＝EN，且直线BM，EN是相交直线
B．BM≠EN，且直线BM，EN是相交直线
C．BM＝EN，且直线BM，EN是异面直线
D．BM≠EN，且直线BM，EN是异面直线
二十．空间中直线与平面之间的位置关系（共1小题）
（多选）29．（2023•沙坪坝区校级模拟）已知α，β是空间中两个不同的平面，m，n是不在平面α，β内的两条不同的直线，则下列推理正确的是（ ）
A．⇒m∥nB．⇒m∥n
C．⇒α∥βD．
二十一．直线与平面平行（共1小题）
30．（2023•白山二模）在正方体ABCD﹣A1B1C1D1中，E，F分别为AB，A1D1的中点，则（ ）
A．EF∥平面BB1D1B．EF∥平面B1CD1
C．EF⊥平面A1BDD．EF⊥平面BC1D
二十二．直线与平面垂直（共2小题）
31．（2023•防城港模拟）一个正三棱台的上、下底面边长分别为3和6，侧棱长为2，则其高为（ ）
A．B．1C．D．
32．（2023•张家口一模）已知正方体ABCD﹣A1B1C1D1，则下列选项不正确的是（ ）
A．直线A1B与B1C所成的角为60°
B．A1B⊥DB1
C．DB1⊥平面ACD1
D．B1C⊥B1D
二十三．平面与平面之间的位置关系（共2小题）
33．（2023•碑林区校级模拟）已知m，n是两条不重合的直线，α，β是两个不重合的平面，下列命题正确的是（ ）
A．若m∥α，m∥β，n∥α，n∥β，则α∥β
B．若m⊥n，m∥α，n⊥β，则α⊥β
C．若m⊥n，m⊂α，n⊂β，则α⊥β
D．若m∥n，m⊥α，n⊥β，则α∥β
34．（2023•汉滨区校级模拟）在正方体ABCD﹣A1B1C1D1中，L，M，N分别为棱A1B1，AD，CC1的中点，则平面LMN与平面CBD1的位置关系是（ ）
A．垂直B．相交不垂直C．平行D．重合
二十四．平面与平面平行（共2小题）
35．（2023•乌鲁木齐模拟）如图，在长方体ABCD﹣A1B1C1D1中，若E，F，G，H分别是棱A1B1，BB1，CC1，C1D1上的动点．且EH∥FG，则必有（ ）
A．BD1⊥EHB．AD∥FG
C．平面BB1D1D⊥平面EFGHD．平面A1BCD1∥平面EFGH
36．（2023•河南模拟）在正方体ABCD﹣A1B1C1D1中，M，N，P分别为A1B，A1C1，A1D的中点，则下列结论中错误的是（ ）
A．MN∥AD1B．平面MNP∥平面BC1D
C．MN⊥CDD．平面MNP⊥平面A1BD
二十五．平面与平面垂直（共2小题）
37．（2023•兴庆区校级模拟）已知直线a，b与平面α，β，γ，能使α⊥β的充分条件是（ ）
A．a∥α，b∥β，a⊥bB．α⊥γ，β⊥γ
C．a∥α，a⊥βD．α∩β＝a，a⊥b，b⊂β
38．（2023•沙坪坝区校级模拟）如图，在五棱锥P﹣ABCDE中，BE∥CD，AB＝BE＝EA＝PD+DE＝PC+CB，∠DEB＝∠CBE＝60°．
（1）证明：BE⊥AP；
（2）若平面PCD⊥平面ABCDE，平面PCB⊥平面PEB，探索：是否为定值？若为定值，请求出的值；若不是定值，请说明理由．
二十六．空间中的点的坐标（共1小题）
39．（2023•东城区校级模拟）在空间直角坐标系O﹣xyz中．正四面体P﹣ABC的顶点A，B分别在x轴，y轴上移动．若该正四面体的棱长是2，则|OP|的取值范围是（ ）
A．[﹣1，+1]B．[1，3]C．[﹣1，2]D．[1，+1]
二十七．空间向量及其线性运算（共2小题）
40．（2023•鼓楼区校级模拟）在三棱锥P﹣ABC中，点O为△ABC的重心，点D，E，F分别为侧棱PA，PB，PC的中点，若，，，则＝（ ）
A．B．
C．D．
41．（2023•湖南模拟）如图，M在四面体OABC的棱BC的中点，点N在线段OM上，且，设，，，则下列向量与相等的向量是（ ）
A．B．C．D．
二十八．空间向量的数量积运算（共2小题）
42．（2023•滁州模拟）已知向量，，若，则x＝（ ）
A．﹣3B．3C．﹣1D．6
43．（2023•海安市校级一模）设向量＝（3，5，2），＝（﹣2，1，3），当数m与n满足下列哪种关系时，向量m+n与x轴垂直（ ）
A．3m＝2nB．3m＝nC．m＝2nD．m＝n
二十九．空间向量的夹角与距离求解公式（共1小题）
44．（2023•小店区校级模拟）如图，在正四棱柱ABCD﹣A1B1C1D1中，AA1＝2，AB＝BC＝1，动点P、Q分别在线段C1D、AC上，则线段PQ长度的最小值是（ ）
A．B．C．D．
三十．空间向量基本定理、正交分解及坐标表示（共2小题）
45．（2023•芦溪县校级一模）若构成空间的一个基底，则下列向量共面的是（ ）
A．，，B．，，
C．，，D．，，
46．（2023•新乡模拟）已知点O、A、B、C为空间不共面的四点，且向量＝++，向量＝+﹣，则与、不能构成空间基底的向量是（ ）
A．B．C．D．或
三十一．向量的数量积判断向量的共线与垂直（共1小题）
47．（2023•湖北模拟）已知向量的夹角为60°，若，则＝（ ）
A．1B．2C．3D．4
三十二．直线的方向向量、空间直线的向量参数方程（共1小题）
48．（2023•琼山区校级三模）直线x﹣3y+1＝0的一个方向向量是（ ）
A．（1，3）B．（3，1）C．（1，﹣3）D．（3，﹣1）
三十三．平面的法向量（共1小题）
49．（2023•盱眙县校级四模）已知平面α内有一个点A（2，﹣1，2），α的一个法向量为＝（3，1，2），则下列点P中，在平面α内的是（ ）
A．（1，﹣1，1）B．C．D．
三十四．直线与平面所成的角（共4小题）
50．（2023•沙坪坝区校级模拟）已知四边形ABCD如图1所示AD∥BC，AB＝AD＝DC＝BC＝2，将△ABD沿BD折起得到四面体A'BCD，如图2所示，．
（1）证明：A′B⊥CD；
（2）求直线A'B与平面A'CD所成角的大小．
51．（2023•平罗县校级模拟）在正方体ABCD﹣A1B1C1D1中，若M点是面BCC1B1的中心，则DM与平面ABCD所成角的余弦值是（ ）
A．B．C．D．
52．（2023•潍坊一模）在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，PC⊥PD，二面角A﹣CD﹣P为直二面角．
（1）求证：PB⊥PD；
（2）当PC＝PD时，求直线PC与平面PAB所成角的正弦值．
53．（2023•陈仓区模拟）如图，在四棱锥P﹣ABCD中，PC⊥平面ABCD，AB∥CD，CD⊥AD，PC＝AB＝2CD＝2，，E是棱PB上一点．
（1）求证：平面EAC⊥平面PBC；
（2）若E是PB的中点，求直线PA与平面EAC所成角的正弦值．
三十五．二面角的平面角及求法（共4小题）
54．（2023•河北三模）如图，在三棱柱ABC﹣A1B1C1中，平面ABC⊥平面 AA1B1B，AC＝BC，四边形AA1B1B是边长为2的菱形，∠BAA1＝60°．
（1）证明：AB⊥A1C；
（2）若A1C⊥BC1，求平面BA1C和平面BA1C1夹角的余弦值．
55．（2023•岳麓区校级模拟）如图，圆台O1O2的轴截面为等腰梯形A1ACC1，AC＝2AA1＝2A1C1＝4，B为下底面圆周上异于A，C的点．
（1）在平面BCC1内，过C1作一条直线与平面A1AB平行，并说明理由；
（2）若四棱锥B﹣A1ACC1的体积为，求平面A1AB与平面C1CB夹角的余弦值．
56．（2023•凉山州模拟）如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥底面ABCD，AB＝PA＝2，且直线PD与底面ABCD所成的角为．
（1）求证：平面PBD⊥平面PAC；
（2）若，求二面角M﹣AC﹣P的余弦值．
57．（2023•沙坪坝区校级二模）如图，在直三棱柱ABC﹣A1B1C1中，AC⊥AB，AC＝2AB＝2AA1＝2，M为AC的中点，A1N⊥B1C1，垂足为N．
（1）求证：B1C∥平面A1BM；
（2）求直线BN与平面A1BM所成角的正弦值；
（3）求平面A1BN与平面A1BM的夹角．
三十六．点、线、面间的距离计算（共3小题）
58．（2023•陈仓区模拟）如图，在四棱锥P﹣ABCD中，四边形ABCD是正方形，PD＝AD＝1，PD⊥平面ABCD，点E是棱PC的中点，点F是棱PB上的一点，且EF⊥PB．
（1）求证：PA∥平面EDB；
（2）求点F到平面EDB的距离．
59．（2023•郑州模拟）在几何体ABC﹣A1B1C1中，AB＝BC＝，AC＝3，点D，E在棱AC上，且AD＝DE＝EC，三棱柱DBE﹣A1B1C1是直三棱柱．
（1）求证：平面A1BE⊥平面ABB1；
（2）若A1D＝2，求点A1到平面AB1C的距离．
60．（2023•周至县三模）如图，在三棱柱ABC﹣A1B1C1中，AA1⊥平面ABC，D，E分别为AC，A1C1的中点，，AC＝AA1＝2．
（Ⅰ）求证：AC⊥平面BDE；
（Ⅱ）求点D到平面ABE的距离．
六、易错分析
一、混淆线面角和平面的法向量与直线方向向量夹角的关系致错
1.如图，在正方体中，E为的中点．求直线与平面所成角的正弦值．
二、忽略两平面法向量的夹角与二面角平面角的关系致错
2、如图所示的几何体是由棱台ABC－A1B1C1和棱锥D－AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=B1C1=1.求二面角A1-BD-C1的余弦值.
三、忽略异面直线所成角与向量夹角的关系致错
3．在长方体ABCD-A1B1C1D1中，AB＝3，BC＝1，AA1＝2，则异面直线BD1和B1C所成角的余弦值为( )
A.eq \f(3\r(70),70) B．－eq \f(3\r(70),70) C．－eq \f(\r(70),70) D.eq \f(\r(70),70)
四、忽视异面直线所成角的范围致错
4．直三棱柱ABC—A′B′C′中，AC＝BC＝AA′，∠ACB＝120°，E为BB′的中点，异面直线CE与C′A所成角的余弦值是（ ）
A． B．C．D．
五、误用垂直性质定理致错
5、已知两个平面垂直，下列命题：
①一个平面内已知直线必垂直于另一个平面内的任意一条直线；
②一个平面内的已知直线必垂直于另一个平面的无数条直线；
③一个平面内的任一条直线必垂直于另一个平面；
④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面．其中正确命题个数是( )
A．3 B．2 C．1 D．0
六、判断线面、线线位置关系考虑不全致错
6．若直线a与平面内无数条直线平行，则a与的位置关系是________．
七、证明线面平行、面面平行条件表达不全致错
7．如图，四棱锥中，四边形ABCD是矩形，，AD＝2，为正三角形，且平面PAD⊥平面ABCD，E、F分别为PC、PB的中点．证明：平面PAD；
八、分析问题不全面致错
8．圆柱的侧面展开图是边长分别为6π和4π的矩形，则圆柱的体积是________．
九、斜二测画法中混淆原图与直观图关系致错
9．如下图，是用“斜二测画法”画出的直观图，其中，，那么的周长是________．
十、混淆几何体的表面积与侧面积致错
10.如图所示的某粮仓(粮仓的底部位于地面上)是由圆柱和圆锥构成的，若圆柱的高是圆锥高的2倍，且圆锥的母线长是4，侧面积是4π，则制作这样一个粮仓的用料面积为( )
A．4eq \r(15)π B．(2eq \r(15)＋4)π
C．(3eq \r(15)＋4)π D．(4eq \r(15)＋4)π
七、刷常考
一．选择题（共8小题）
1．（2023•辽宁二模）已知某圆锥的高为，体积为，则该圆锥的侧面积为（ ）
A．B．3πcm2C．6πcm2D．12πcm2
2．（2023•道里区校级一模）将一个底面半径为1，高为2的圆锥形工件切割成一个圆柱体，能切割出的圆柱最大体积为（ ）
A．B．C．D．
3．（2023•岳阳县模拟）空间中，α，β，γ是三个互不重合的平面，l是一条直线，则下列命题中正确的是（ ）
A．若α⊥β，l∥α，则l⊥βB．若α⊥β，l⊥β，则l∥α
C．若l⊥α，l∥β，则α⊥βD．若l∥α，l∥β，则α∥β
4．（2023•喀什地区模拟）如图，在正四棱柱ABCD﹣A1B1C1D1中，底面边长为2，直线CC1与平面ACD1所成角的正弦值为，则正四棱柱的高为（ ）
A．2B．3C．4D．5
5．（2023•商洛三模）在四面体ABCD中，AB⊥BC，AB⊥AD，向量与的夹角为，若AB＝6，BC＝AD＝3，则该四面体外接球的表面积为（ ）
A．18πB．36πC．54πD．72π
6．（2023•浙江模拟）如图1，直角梯形ABCD中，，取AB中点E，将△BCE沿EC翻折（如图2），记四面体B﹣ECD的外接球为球O（O为球心）．P是球O上一动点，当直线AO与直线AP所成角最大时，四面体P﹣AEC体积的最大值为（ ）
A．B．C．D．
7．（2023•道里区校级一模）在边长为3的菱形ABCD中，∠BAD＝60°，将△ABD绕直线BD旋转到．△A'BD，使得四面体A'BCD外接球的表面积为18π，则此时二面角A'﹣BD﹣C的余弦值为（ ）
A．﹣B．﹣C．D．
8．（2023•鹰潭二模）如图，在棱长为2的正四面体ABCD中，点N，M分别为△ABC和△ABD的重心，P为线段CM上一点，（ ）
A．AP+BP的最小为2
B．若DP⊥平面ABC，则
C．若DP⊥平面ABC，则三棱锥P﹣ABC外接球的表面积为
D．若F为线段EN的中点，且DP∥MF，则MP＝MC
二．多选题（共4小题）
（多选）9．（2023•南关区校级模拟）如图，平面四边形ABCD中，△BCD是等边三角形，AB⊥BD且AB＝BD＝2，M是AD的中点．沿BD将△BCD翻折，折成三棱锥C﹣ABD，在翻折过程中，下列结论正确的是（ ）
A．存在某个位置，使得CM与BD所成角为锐角
B．棱CD上总会有一点N，使得MN∥平面ABC
C．当三棱锥C﹣ABD的体积最大时，AB⊥BC
D．当平面ABD⊥平面BDC时，三棱锥C﹣ABD的外接球的表面积是8π
（多选）10．（2023•二模拟）已知a，b，l为不同的直线，α，β，γ为不同的平面，则下列说法正确的是（ ）
A．若α∥β，a⊂α，b⊂β，则a∥b
B．若a⊥α，b⊂β，α∥β，则
C．若α⊥β，α∩β＝l，a⊂α，b⊂β，a⊥b，则a，b至少有一条与直线l垂直
D．若α⊥β，α⊥γ，β∩γ＝l，则l⊥α
（多选）11．（2023•亭湖区校级三模）我国古代数学名著《九章算术》中将“底面为直角三角形且侧棱垂直于底面的三棱柱”称为“堑堵”．现有一如图所示的“暂堵”ABC﹣A1B1C1，其中AB⊥BC，若BB1＝AB＝2，BC＝1，则（ ）
A．该“堑堵”的体积为2
B．该“堑堵”外接球的表面积为9π
C．若点P在该“堑堵”上运动，则|PA|的最大值为
D．该“堑堵”上，AC1与平面BB1C1C所成角的正切值为
（多选）12．（2023•鼓楼区校级模拟）已知正方体ABCD﹣A1B1C1D1的棱长为2（如图所示），点M为线段CC1（含端点）上的动点，由点A，D1，M确定的平面为α，则下列说法正确的是（ ）
A．平面α截正方体的截面始终为四边形
B．点M运动过程中，三棱锥A1﹣AD1M的体积为定值
C．平面α截正方体的截面面积的最大值为
D．三棱锥A1﹣AD1M的外接球表面积的取值范围为
三．填空题（共4小题）
13．（2023•广陵区校级模拟）水平桌面上放置了4个半径为2的小球，4个小球的球心构成正方形，且相邻的两个小球相切．若用一个半球形的容器罩住四个小球，则半球形容器内壁的半径的最小值为 ．
14．（2023•九江三模）如图，棱长为2的正方体ABCD﹣A1B1C1D1中，P，Q为四边形ABC1D1内的点（包括边界），且点P到AB的距离等于到平面A1B1C1D1的距离，点Q到C1D1的距离等于到平面ABCD的距离，则|PQ|的最小值为 ．
15．（2023•郑州模拟）在正四棱柱ABCD﹣A1B1C1D1中，AB＝4，点E为A1B1中点，点F为AD中点，直线B1C与直线EF所成角的余弦值为，过E、F、C1做该正四棱柱的截面，则截面周长为 ．
16．（2023•宣威市校级模拟）所谓正三棱锥，指的是底面为正三角形，顶点在底面上的射影为底面三角形中心的三棱锥，在正三棱锥P﹣ABC中，M是PC的中点，且AM⊥PB，底面边长，则正三棱锥P﹣ABC的外接球的表面积为 ；AM与底面ABC所成角的正弦值为 ．
四．解答题（共10小题）
17．（2023•海淀区校级三模）如图1，在直角梯形ABCD中，AD∥BC，AD＝AB＝，∠BAD＝90°，∠BCD＝45°，E为对角线BD的中点．现将△ABD沿BD折起到△PBD的位置，使平面PBD⊥平面BCD，如图2．
（Ⅰ）求证直线PE⊥平面BCD；
（Ⅱ）求异面直线BD和PC所成角的余弦值；
（Ⅲ）已知空间存在一点Q到点P，B，C，D的距离相等，写出这个距离的值（不用说明理由）．
18．（2023•芦溪县校级一模）如图，已知四棱锥P一ABCD的底面为直角梯形，AB∥CD，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝AB＝1．M是PB的中点．
（1）求证AM＝CM；
（2）N是PC的中点，求证DN∥平面AMC．
19．（2023•温州模拟）如图，在四棱锥P﹣ABCD中，AB∥CD，∠ABC＝90°，△ADP是等边三角形，AB＝AP＝2，BP＝3，AD⊥BP．
（Ⅰ）求BC的长度；
（Ⅱ）求直线BC与平面ADP所成的角的正弦值．
20．（2023•广陵区校级模拟）如图，菱形ABCD与四边形BDEF相交于BD，∠ABC＝120°，BF⊥平面ABCD，DE∥BF，BF＝2DE，AF⊥FC，M为CF的中点，AC∩BD＝G．
（I）求证：GM∥平面CDE；
（II）求直线AM与平面ACE所成角的正弦值．
21．（2023•泉州模拟）如图，已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝1，AB⊥AC，M，N分别是CC1，BC的中点，点P在直线A1B1上．
（1）证明：PN⊥AM；
（2）当平面PMN与平面ABC所成的锐二面角为45°时，求平面PMN与侧面A1ACC1的交线长．
22．（2023•天津模拟）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BCA＝60°，AP＝AC＝AD＝2，E为CD的中点，M在AB上，且＝2．
（Ⅰ）求证：EM∥平面PAD；
（Ⅱ）求平面PAD与平面PBC所成锐二面角的余弦值；
（Ⅲ）点F是线段PD上异于两端点的任意一点，若满足异面直线EF与AC所成角45°，求AF的长．
23．（2023•海淀区模拟）如图，空间几何体由两部分构成，上部是一个底面半径为1，高为2的圆锥，下部是一个底面半径为1，高为2的圆柱，圆锥和圆柱的轴在同一直线上，圆锥的下底面与圆柱的上底面重合，点P是圆锥的顶点，AB是圆柱下底面的一条直径，AA1、BB1是圆柱的两条母线，C是弧的中点．
（1）求异面直线PA1与BC所成的角的大小；
（2）求点B1到平面PAC的距离．
24．（2023•市中区校级模拟）在直角梯形AA1B1B中，A1B1∥AB，AA1⊥AB，AB＝AA1＝2A1B1＝6，直角梯形AA1B1B绕直角边AA1旋转一周得到如下图的圆台A1A，已知点P，Q分别在线段CC1，BC上，二面角B1﹣AA1﹣C1的大小为θ．
（1）若θ＝120°，，AQ⊥AB，证明：PQ∥平面AA1B1B；
（2）若θ＝90°，点P为CC1上的动点，点Q为BC的中点，求PQ与平面AA1C1C所成最大角的正切值，并求此时二面角Q﹣AP﹣C的余弦值．
25．（2023•分宜县校级一模）在正△ABC中，E，F，P分别是AB，AC，BC边上的点，满足，将△AEF沿EF折起到△A1EF的位置，使二面角A1﹣EF﹣B成直二面角，连接A1B，A1P．
（1）求证：A1E⊥平面BEP；
（2）求直线A1E与平面A1BP所成角的大小．
26．（2023•天津模拟）如图，在三棱锥S﹣ABC中，SC⊥平面ABC，SC＝3，AC⊥BC，CE＝2EB＝2，AC＝，CD＝ED．
（Ⅰ）求证：DE⊥平面SCD；
（Ⅱ）求二面角A﹣SD﹣C的余弦值；
（Ⅲ）求点A到平面SCD的距离．