人教版（2024）七年级下册（2024）第七章 相交线与平行线7.2 平行线7.2.2 平行线的判定导学案

这是一份人教版（2024）七年级下册（2024）第七章 相交线与平行线7.2 平行线7.2.2 平行线的判定导学案，共11页。学案主要包含了教学目标，教学重，教学过程，教学反思等内容，欢迎下载使用。
一、教学目标：
1.掌握平行线的三种判定方法，会运用判定方法来判断两条直线是否平行；
2.能够根据平行线的判定方法进行简单的推理.
二、教学重、难点：
重点：理解直线平行的判定方法，并会根据判定方法进行简单的推理应用.
难点：平行线判定方法的灵活运用和其推导过程中的转化思想的认识.
三、教学过程：
复习回顾
1.平行线定义：在同一个平面内，不相交的两条直线叫做平行线. 记作：a∥b.
2.基本事实(平行公理)：经过直线外一点，有且只有一条直线与这条直线平行.
3.平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行.(也就是说：如果b∥a，c∥a，那么b∥c.几何语言：∵ b∥a，c∥a，∴ b∥c.)
如何用直尺和三角板过直线AB外一点P做AB的平行线CD.

知识精讲
思考：在用直尺和三角尺画平行线的过程中，直尺和三角尺分别起着什么样的作用？
可以看出，画直线AB的平行线CD，实际上就是过点P画与∠2相等的∠1，而∠2和
∠1正是直线AB，CD被直线EF截得的同位角，这说明，如果同位角相等，那么AB∥CD.
判定方法1：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.
简单说成：同位角相等，两直线平行.
几何语言：
∵ ∠1=∠2 ∴ AB∥CD
如图，你能说出木工用图中的角尺画平行线的道理吗？
∵ ∠BEF=∠ECD
∴ CD∥EF (同位角相等，两直线平行)
思考：两条直线被第三条直线所截，同时得到同位角、内错角和同旁内角. 由同位角相等，可以判定两条直线平行，那么，能否利用内错角，或同旁内角来判定两直线平行呢？
猜一猜：
(1) 内错角满足什么关系时？两直线会平行？
(2) 同旁内角满足什么关系时？两直线会平行？
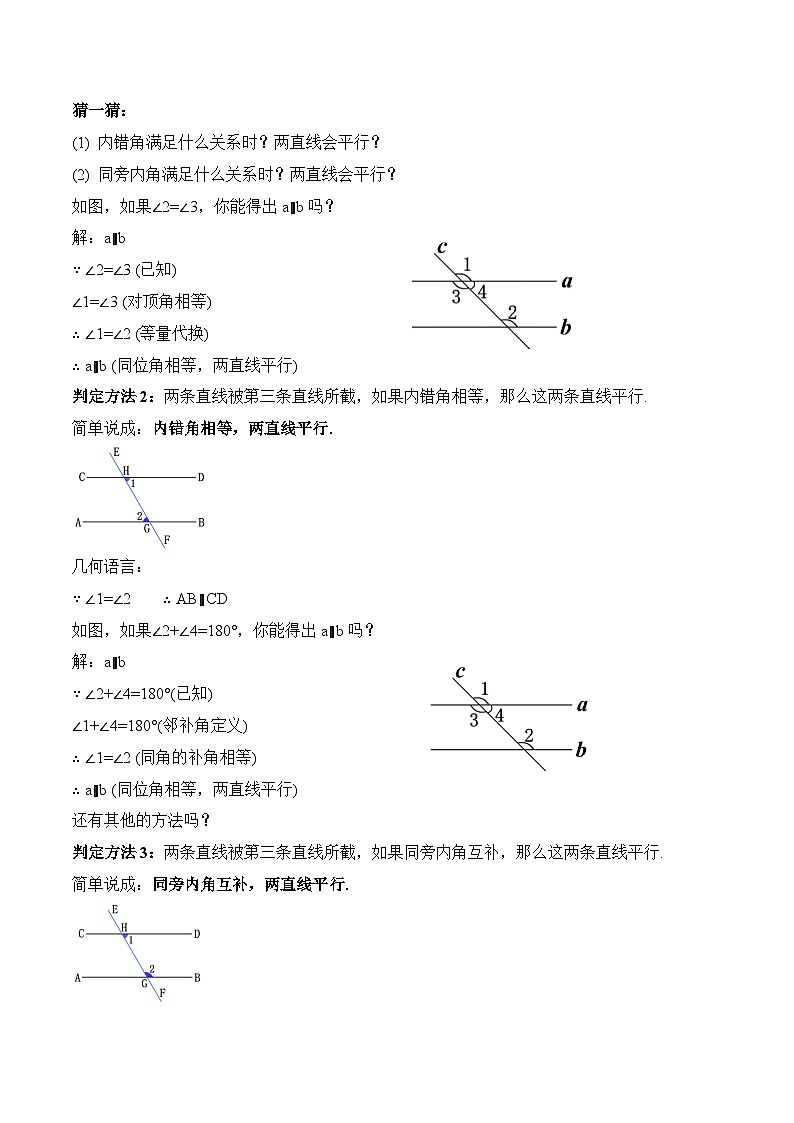
如图，如果∠2=∠3，你能得出a∥b吗？
解：a∥b
∵ ∠2=∠3 (已知)
∠1=∠3 (对顶角相等)
∴ ∠1=∠2 (等量代换)
∴ a∥b (同位角相等，两直线平行)
判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
简单说成：内错角相等，两直线平行.
几何语言：
∵ ∠1=∠2 ∴ AB∥CD
如图，如果∠2+∠4=180°，你能得出a∥b吗？
解：a∥b
∵ ∠2+∠4=180°(已知)
∠1+∠4=180°(邻补角定义)
∴ ∠1=∠2 (同角的补角相等)
∴ a∥b (同位角相等，两直线平行)
还有其他的方法吗？
判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
几何语言：
∵ ∠1+∠2=180° ∴ AB∥CD
感悟：遇到一个新问题时，常常把它转化为已知的(或已经解决的)问题来解决. 这一节中，我们利用“同位角相等，两直线平行”得到了“内错角相等，两直线平行”和“同旁内角互补，两直线平行”.因此，在解题的过程中，可以用这种思路去分析实际问题，从而解决问题.
【归纳】
同位角相等，两直线平行.
内错角相等，两直线平行.
同旁内角互补，两直线平行.
几何语言：
判定1：∵ ∠1=∠2 ∴ AB∥CD
判定2：∵ ∠1=∠4 ∴ AB∥CD
判定3：∵ ∠1+∠3=180° ∴ AB∥CD
典例解析
例1.如图，AB⊥EF于点B，CD⊥EF于点D，∠1＝∠2，试判断BM与DN是否平行，为什么？
解：BM∥DN；理由如下：
∵AB⊥EF，CD⊥EF，
∴∠ABE＝∠CDE＝90°(垂直的定义)，
∵∠1＝∠2，
∴∠ABE－∠1＝∠CDE－∠2，
即∠MBE＝∠NDE，
∴BM∥DN (同位角相等，两直线平行)．
【针对练习】已知：如图，CF平分∠ACM，∠1=72°，∠2=36°，判断CM与DN是否平行，并说明理由．
解：CM∥DN
∵CF平分∠ACM
∴∠ACM=2∠1
∵∠1=72°
∴∠ACM=2∠1=144°
∴∠BCM=180°-144°=36°
∵∠2=36°，
∴∠2 =∠BCM．
∴CM∥DN
例2.如图，点G在CD上，已知∠BAG+∠AGD=180°，EA平分∠BAG，FG平分∠AGC．
请说明AE∥GF的理由．
解：因为∠BAG+∠AGD=180°(已知)，
∠AGC+∠AGD=180°(___________)，
所以∠BAG=∠AGC(_______________)．
因为EA平分∠BAG，
所以∠1=12∠BAG(________________)．
因为FG平分∠AGC，
所以∠2=12________，
得∠1=∠2(等量代换)，
所以_________(________________________)．
【针对练习】已知如图所示，∠B=∠C，点B、A、E在同一条直线上，∠EAC=∠B+∠C，且AD平分∠EAC，试说明AD∥BC的理由．
解：理由如下：
∵AD平分∠EAC，
∴∠1＝12∠EAC，
∵∠EAC＝∠B＋∠C，∠B＝∠C，
∴∠C＝12∠EAC，
∴∠C＝∠1，
∴AD∥BC．
例3.如图，已知∠1=∠3，∠1+∠2=180°．
(1)试判断BF与DE的位置关系，并说明理由；
(2)若BF⊥AC，∠2=140°，求∠AFG的度数．
（1）解：BF∥DE，理由如下：
∵∠1=∠3，∠1+∠2=180°．
∴∠3+∠2=180°．
∴BF∥DE；
（2）解：∵∠1+∠2=180°，∠2=140°，
∴∠1=40°，
∵BF⊥AC，
∴∠AFB=90°，
∴∠AFG=∠AFB-∠1=50°．
【针对练习】如图，已知∠A=∠C，∠1与∠2互补，试说明AB和CD的位置关系并说明理由．
解：AB∥CD，理由如下：
∵∠1与∠2互补，即∠1+∠2=180°，
∴AD∥BC，
∴∠A+∠ABC=180°，
∵∠A=∠C，
∴∠C+∠ABC=180°，
∴AB∥CD．
课堂小结
1.本节课你有哪些收获？2.还有没解决的问题吗？
【设计意图】培养学生概括的能力。使知识形成体系，并渗透数学思想方法。
达标检测
1.如图所示，直线a,b被c所截，现给出下列四个条件:
①∠1=∠5；②∠3+∠6=180°；③∠2+∠3=180°；④∠4=∠5.其中能判定a//b的条件有序号是( )
A.①② B.①③ C.①④ D.③④
2.如图，下列条件中,能判断直线.l1//l2的是( )
A.∠2=∠3 B.∠1=∠3 C.∠4+∠5=180° D.∠2=∠4
3.如图，下列条件中，能判断直线l1//l2的是( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
4.如图，下列结论中正确的是( )
A.若∠1=∠4，则m//c B.若∠1=∠2，则a//b
C.若∠1+∠3=180，则n//c D.若∠2+∠3=180°，则m//n
5.如图(1)，光线AB,CD被一个平面镜反射，此时∠1=∠3,∠2=∠4，则AB // _____,BE_____DF.
6.如图(2)，已知∠C=100°，若增加一个条件，使得AB // CD,试写出符合要求的一个条件:___________________.
7.如图，∠B=∠3,则____//_____，根据的是__________________________;若∠2=∠A，则____//_____，根据的是_______________________________;若∠2=∠E，则____//_____，根据的是_______________________________;若∠B+∠BCE=180°,则____//_____，根据
的是________________________________.
8.如图，BE是AB的延长线.
(1)由∠CBE=∠A可以判定哪两条直线平行？根据什么？
(2)由∠CBE=∠C可以判定哪两条直线平行？根据什么？
9.如图，∠1=∠2=55°，∠3等于多少度?直线AB、CD平行吗?说明你的理由.
10.如图，已知∠B=60°，∠ADE是∠B的2倍,那么直线EF与BC平行吗?请说明理由.
11.小明有一块小画板，他想知道它的上、下边缘是否平行，而小明身边只有一个量角器，你能帮他解决这一问题吗?
【参考答案】
A
B
C
C
CD,∥
∠FEB=100°
AB,CE, 同位角相等，两直线平行;AB,CE,内错角相等，两直线平行;AC,DE, 内错角相等，
两直线平行;AB,CE, 同旁内角互补，两直线平行.
8. 解：(1)∵ ∠CBE=∠A
∴ AD∥BC(同位角相等，两直线平行)
(2)∵ ∠CBE=∠C
∴ CD∥AE(内错角相等，两直线平行)
9. 解: ∠3=55°，AB//CD.
∵ ∠l=∠2=55°(已知)
∠2=∠3 (对顶角相等)
∴ ∠3=∠1=55°(等量代换)
∴ AB//CD (同位角相等，两直线平行)
10. 解: EF//BC.
∵ ∠B=60° (已知)
∴ ∠ADE=2∠B=120° (已知)
∴ ∠BDF=∠ADE=120° (对顶角相等)
∴ ∠B+∠BDF=180° (等式的性质)
∴ EF//BC (同旁内角互补，两直线平行)
11. 解:在上、下边缘之间画一条线段AB(如图所示),得到四个角.利用量角器测量出∠1和∠4(或∠1和∠3或∠2和∠3或∠2和∠4)中的一组角的度数.然后利用内错角相等，两直线平行或同旁内角互补，两直线平行来判定上、下边缘是否平行.
四、教学反思：
平行线的判定是平行线内容的进一步拓展，是进一步学习平行线的有力工具，为学习平行线的性质、三角形、四边形等知识打下基础，在整个初中几何中占有非常重要的地位. 学生虽然已经学了平行线的定义、平行公理，具备了探究直线平行的基础，但学生在文字语言、符号语言和图形语言之间的转换能力比较薄弱，在逻辑思维和合作交流的意识方面发展不够均衡，还需逐渐提高.