人教版（2024）七年级下册（2024）7.2.2 平行线的判定导学案及答案

这是一份人教版（2024）七年级下册（2024）7.2.2 平行线的判定导学案及答案，共7页。学案主要包含了学习目标，学习过程等内容，欢迎下载使用。
一、学习目标：
1.进一步熟悉平行线的判定方法和性质；
2.运用平行线的性质和判定进行简单的推理和计算；（重点、难点）
重点：掌握平行线的性质与判定的综合运用；
难点：会用平行线的性质与判定进行较复杂的推理和计算.
二、学习过程：
复习回顾
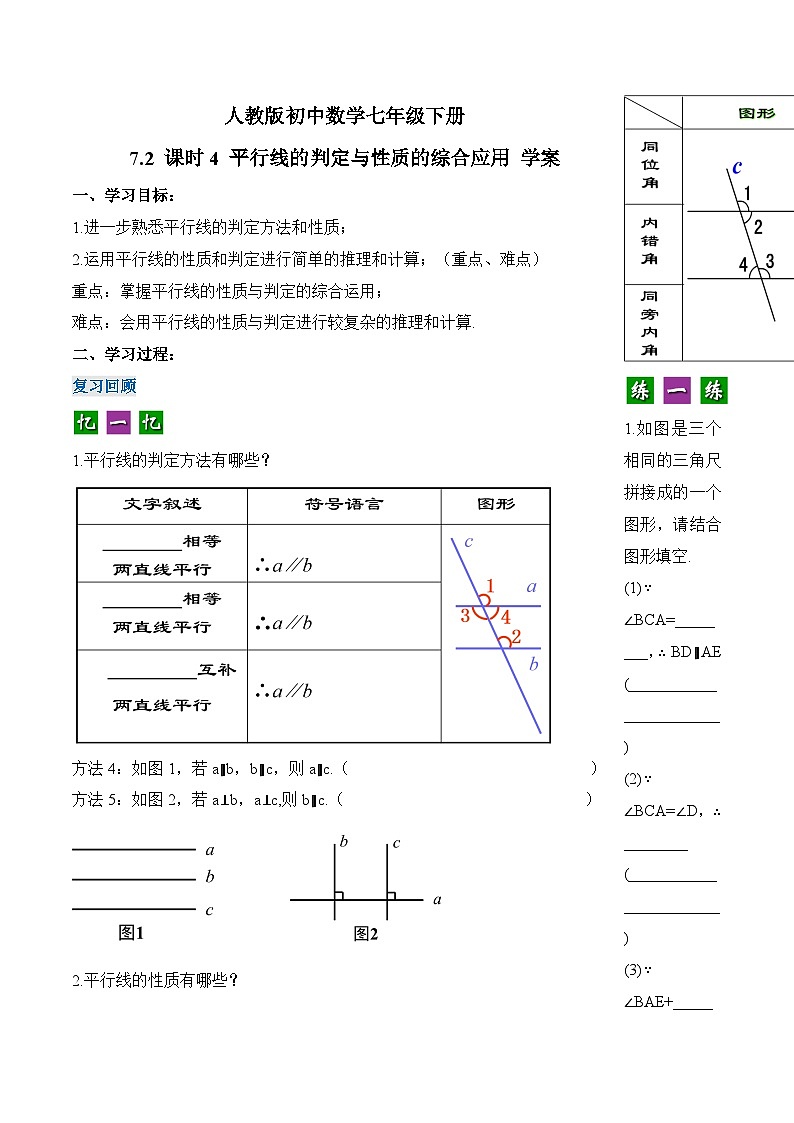
1.平行线的判定方法有哪些？
方法4：如图1，若a∥b，b∥c，则a∥c.（ ）
方法5：如图2，若a⊥b，a⊥c,则b∥c.（ ）

2.平行线的性质有哪些？
1.如图是三个相同的三角尺拼接成的一个图形，请结合图形填空.
(1)∵ ∠BCA=________，∴ BD∥AE (_______________________)
(2)∵ ∠BCA=∠D，∴ ________ (_______________________)
(3)∵ ∠BAE+_______=180°，∴ AB∥CE (_________________________)
2.如图，AB∥CD，CE∥BF，试说明∠1=∠2.
解：∵ AB∥CD (已知)
∴ ∠2=____(_______________________)
∵ CE∥BF (已知)
∴ ∠1=____(_______________________)
∴ ________ (等量代换)
典例解析
例1.如图，已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程，并填写理由或数学式:
解:∵∠3=∠4(已知),
∴AE //_____(________________________).
∴∠EDC=∠5(________________________).
∴∠5=∠A(已知)，
∴∠EDC=______(__________).
∴DC//AB(_______________________).
∴∠5+∠ABC=180°(________________________)，即∠5+∠2+∠3=180°
∵∠1=∠2(已知)，
∴∠5+∠1+∠3=180°(_________)，
即∠BCF+∠3=180°.
∴BE//CF(_________________________).
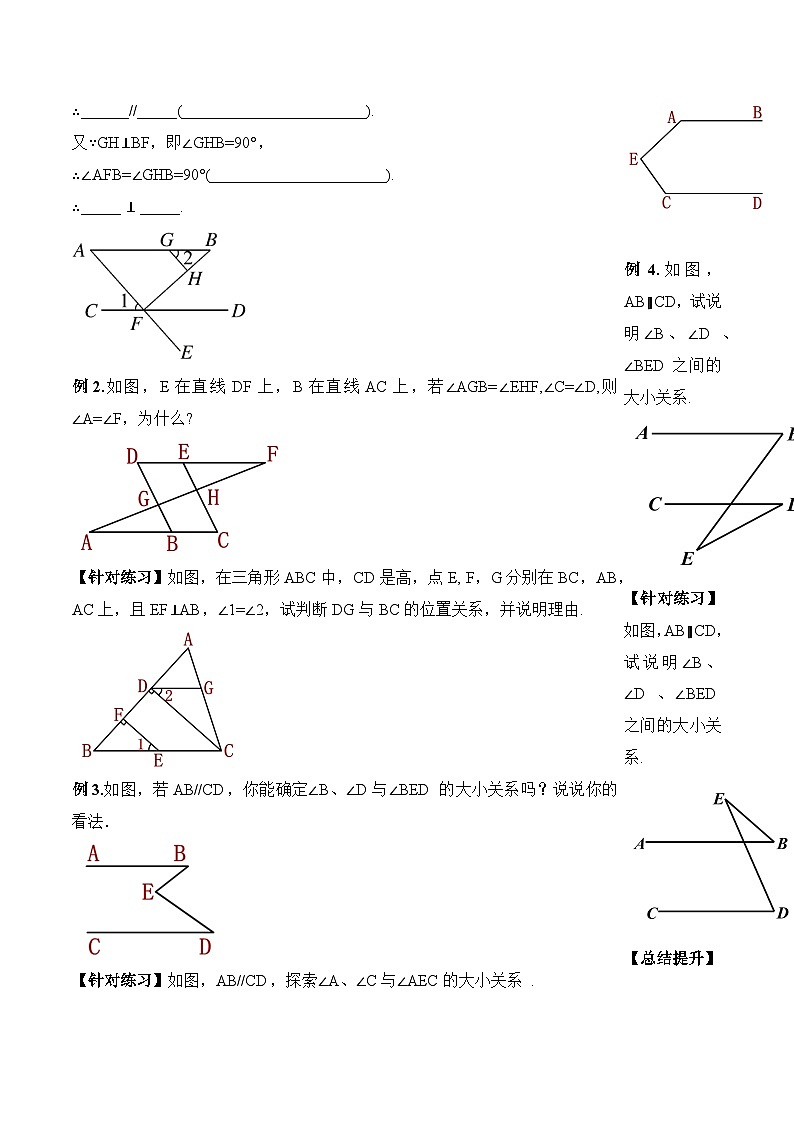
【针对练习】如图,AB//CD，AE交CD于点F，点G在AB上，GH⊥BF，垂足为H,∠1=∠2，试说明AE⊥BF.请将下面的解答过程补充完整(填数字式子或理由).
解:∵AB//CD(已知)，
∴∠1=______(________________________).
∵∠1=∠2(已知)，
∴_____=______(_________).
∴______//_____(_______________________).
又∵GH⊥BF，即∠GHB=90°，
∴∠AFB=∠GHB=90°(______________________).
∴_____ ⊥ _____.
例2.如图，E在直线DF上，B在直线AC上，若∠AGB=∠EHF,∠C=∠D,则∠A=∠F，为什么?
【针对练习】如图，在三角形ABC中，CD是高，点E, F，G分别在BC，AB，AC上，且EF⊥AB，∠1=∠2，试判断DG与BC的位置关系，并说明理由.
例3.如图，若AB//CD，你能确定∠B、∠D与∠BED 的大小关系吗？说说你的看法．
【针对练习】如图，AB//CD，探索∠A、∠C与∠AEC的大小关系 .
例4.如图，AB∥CD，试说明∠B、∠D 、∠BED之间的大小关系.
【针对练习】如图，AB∥CD，试说明∠B、∠D 、∠BED之间的大小关系.
【总结提升】
_______________ _______________ _______________ _______________
达标检测
1.如图(1)，已知∠1=∠2， ∠3=80°， 则∠4等于( )
A. 80° B.70° C.60° D.50°
2.如图(2),直线a,b,c,d,已知c⊥a, c⊥b，直线b,c,d交于一点,若∠1=50°则∠2等于( )
A.45° B.50° C.60° D.75°
3.如图，AB//CD，则α, β, γ之间的等量关系为( )
A. α +β+ γ =360° B. α -β+ γ =180°
C. α +β- γ =180° D. α +β+ γ =180°
4.如图,AB//EF ,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120° B.130° C.140° D.150°
5.如图,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上.若∠1=35°,则∠2的度数为( )
A.10° B.25° C.30° D.35°
6.如图(1)所示，直线a//b,直线c与直线a,b分别相交于点A，B,AM⊥b，垂足为点M,若∠1=58°,则∠2=______.
7.如图(2)所示，若∠1=40°，∠2=40°，∠3=116°40′，则∠4=_______.
8.如图(3)所示，EF//ON，OE平分∠M0N，∠FEO=28°，则∠MFE=____.
9.如图，三角形ABC中，D是AB上一点，E是AC上一点，∠ADE=60°，∠B=60°，∠AED=40°.
(1)DE和BC平行吗？为什么？
(2)∠C是多少度？为什么？
10.如图,在△ABC中，点D、E分别在BC、AB上,且EF//AD,∠1+∠2=180°.
(1)试猜想∠2与∠BAD的关系,并说明理由;
(2)若DG平分∠ADC,试说明:DG // AB.
11.如图,AB//CD,点C在BE上,AE交CD于点F,∠1=∠2,∠3=∠4,试说明:AD//BE.
12.已知直线AB//CD,点M,N分别在直线AB,CD上,点P是平面内一个动点,且满足∠MPN=90°,过点N作射线NQ，使得∠PNQ=∠PNC.
(1)如图①,当射线NQ与NM重合,∠QND=50°时，则∠AMP=______;
(2)如图②,当射线NQ与NM不重合，∠QND=α时,求∠AMP的度数(用含α的式子表示);
(3)请直接写出在点P运动的过程中，∠QND与∠AMP之间的数量关系_______________.