初中数学1.2.3绝对值课文内容ppt课件

这是一份初中数学1.2.3绝对值课文内容ppt课件，文件包含新湘教版初中数学七年级上册123《绝对值》课件pptx、新湘教版初中数学七年上册123《绝对值》教案docx等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
1、了解绝对值的表示法，会计算有理数的绝对值，能利用数形结合思想来理解绝对值的几何定义，理解绝对值非负的意义。2、了通过教学培养分析问题，解决实际问题，读图分析、收集处理信息、团结协作、语言表达的能力。3.通过对绝对值的教学，认识数学知识来源于实践，从现实生活的经历与体验出发，激发对数学问题的兴趣。
正确理解绝对值的概念，能求一个数的绝对值。 
正确理解绝对值的几何意义和代数意义。 
想一想：什么是相反数？
如果两个数只有符号不同，那么其中一个数叫作另一个数的相反数，也称这两个数互为相反数 。
正数的相反数是_______； 0的相反数是_______；负数的相反数是_______；
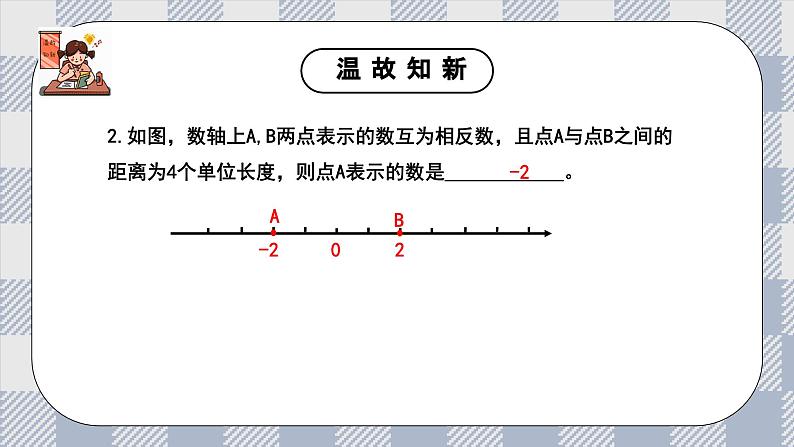
2.如图，数轴上A,B两点表示的数互为相反数，且点A与点B之间的距离为4个单位长度，则点A表示的数是 。
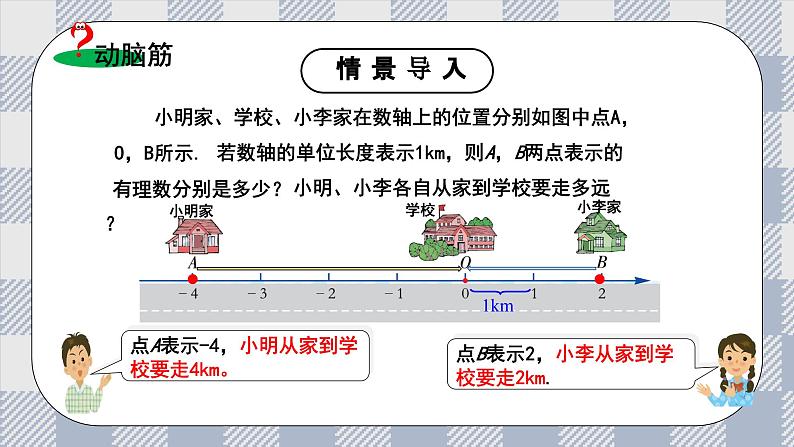
小明家、学校、小李家在数轴上的位置分别如图中点A， O，B所示.
若数轴的单位长度表示1km，则A，B两点表示的有理数分别是多少？
小明、小李各自从家到学校要走多远？
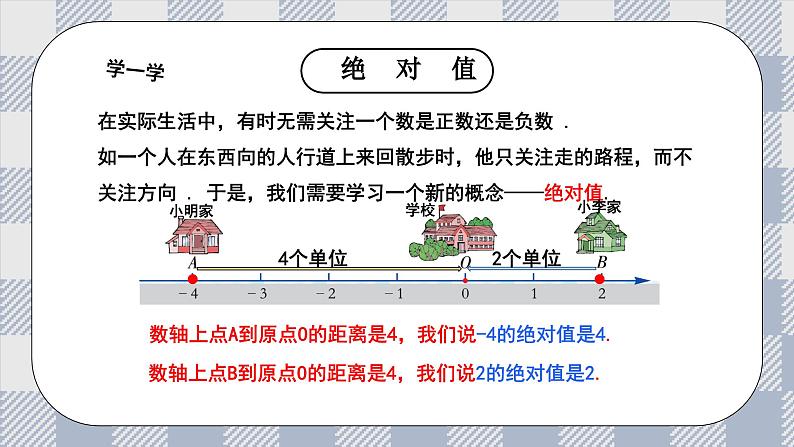
在实际生活中，有时无需关注一个数是正数还是负数 .如一个人在东西向的人行道上来回散步时，他只关注走的路程，而不关注方向 . 于是，我们需要学习一个新的概念——绝对值.
数轴上点A到原点O的距离是4，我们说-4的绝对值是4.
数轴上点B到原点O的距离是4，我们说2的绝对值是2.
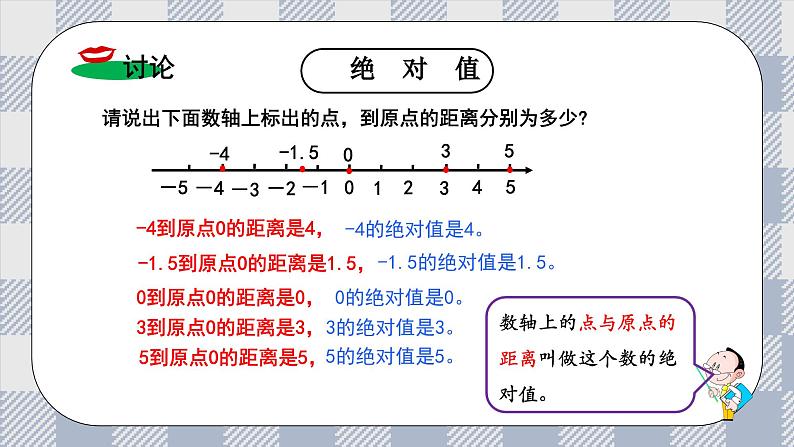
请说出下面数轴上标出的点，到原点的距离分别为多少?
-4到原点O的距离是4，
-1.5到原点O的距离是1.5，
0到原点O的距离是0，
3到原点O的距离是3，
5到原点O的距离是5，
-1.5的绝对值是1.5。
一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作│a│，读作“a的绝对值”.
例如：-4的绝对值记作：|-4|；
0的绝对值记作：|0|；
3的绝对值记作：|3|。
-1.5的绝对值是1.5
记作： |-4| = 4
记作： |-1.5|= 1.5
记作： | 0 |= 0
记作： | 3 |= 3
记作： | 5 |= 5
负数的绝对值等于它的相反数
正数的绝对值等于它的本身
正数的绝对值是它本身.
负数的绝对值是它的相反数.
非负数的绝对值等于它本身
非正数的绝对值等于它的相反数
解：|0.36|=0.36；
|-7.5|=7.5；
如果a表示一个数，则│a│等于多少？
（1） 当a是正数时， │a│= a；（2） 当a = 0时，│a│= 0；（3） 当a是负数时，│a│=-a.
画一条数轴，用数轴上的点表示 4，-4，2，-2，并求这些点与原点的距离.
解：-4到原点的距离是4；
-2到原点的距离是2；
4到原点的距离是4；
2到原点的距离是2；
例6 若 │a│= 8.7，求a.
解：因为绝对值等于8.7的有理数有8.7和-8.7两个，
所以a = 8.7或a =-8.7。
解：|3|=3； |3.14|=3.14
3.画一条数轴，并分别标出表示绝对值等于2，3.5的数的点.
解：绝对值等于2的数是-2和2；绝对值等于3.5的数是-3.5和3.5。
∴绝对值等于2，3.5的数的点在数轴上表示如下：
1.如图，数轴上有A，B，C，D 四个点，其中绝对值小于2的数对应的点是( )A. 点A； B. 点B； C. 点C； D. 点D。
2.若│a│=│b│，则a和b的关系为( )A. a和b相等； B. a和b互为相反数；C. a和b相等或互为相反数； D. 以上答案都不对
3.某交警每天都骑摩托车沿南北街来回巡逻. 假定向北为正方向，当天巡逻记录如下(单位：千米)：15，-9，18，-7，13，-6，10，-6. 则这位交警这一天骑摩托车行了多远？
解：由题意得： │15│+│-9│+│18│+│-7│+│13│ +│-6│ +│10│ +│-6│ =15+9+18+7+13+6+10+6=84(千米)， 答：这位交警这一天骑摩托车行了84千米。
一个数的绝对值就是表示这个数的点到原点的距离
互为相反数的绝对值的特点
互为相反数的绝对值相等
课堂作业：P12习题1.2第6、7、8题；
课后作业：P12习题1.2第10、12、13题，预习P14~16《有理数大 小的比较》