初中数学冀教版（2024）七年级下册（2024）第十一章 一元一次不等式和一元一次不等式组11.3 解一元一次不等式课文课件ppt

这是一份初中数学冀教版（2024）七年级下册（2024）第十一章 一元一次不等式和一元一次不等式组11.3 解一元一次不等式课文课件ppt，文件包含第1课时一元一次不等式的有关概念pptx、第2课时解一元一次不等式pptx、113解一元一次不等式doc等3份课件配套教学资源，其中PPT共64页， 欢迎下载使用。
1. 理解不等式的解、解集以及解不等式这些概念的 含义.2. 能用数轴正确表示不等式的解集.（重、难点）3. 掌握一元一次不等式的概念，并能利用不等式 的性质解简单的一元一次不等式.（重点）
天平左边质量为60(x+1)，天平右边质量为80x，你能判断哪边的质量大，并列出不等式吗？
80x>60(x+1)
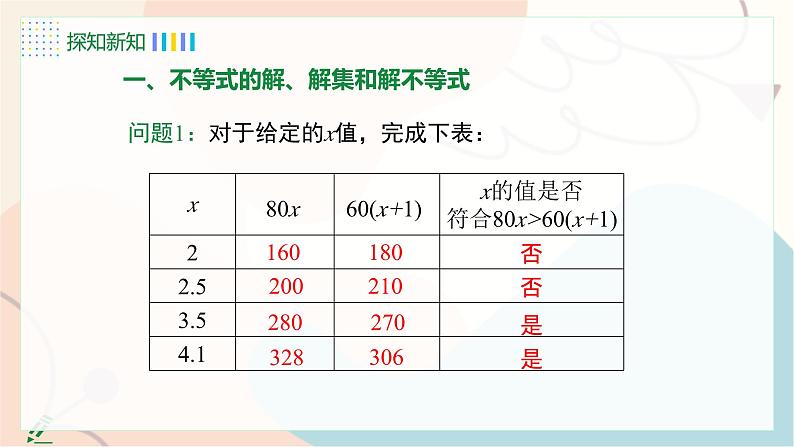
一、不等式的解、解集和解不等式
问题1：对于给定的x值，完成下表：
对于含有未知数的不等式，能使不等式成立的未知数的值，叫做不等式的解.
问题2：上述数值3.5，4.1都满足不等式80x>60(x+1)，那么我们可以把这些数值叫做什么？
问题3：数4,5，5.5是不等式80x>60(x+1)的解吗？你认为不等式80x>60(x+1)的解有多少个？
一个含有未知数的不等式的所有解组成这个不等式的解集.
求不等式解集的过程，叫做解不等式.
下列不等式中，不含有x=-1这个解的是 （ ）
A. 2x+1≤-3 B. 2x-1≥-3C. -2x+1≥3 D. -2x-1≤3
二、在数轴上表示不等式的解集
则点A右边所有的点表示的数都大于3，而点A左边所有的点表示的数都小于3
先在数轴上标出表示3的点A
例如，不等式80x>60(x+1)的解集为x>3.
问题：解集包含这么多数，该怎么表示解集呢？
因此可以像图那样表示解集x>3.
则点B右边所有的点表示的数都大于-1，而点B左边所有的点表示的数都小于-1
同理，不等式-2x≥2的解集为x≤-1.
先在数轴上标出表示-1的点B
因此可以像图那样表示解集x≤-1.
在数轴上表示下列不等式的解集：(1)x＞－3； (2)x≤2.
(1)x＞－3可用数轴上表示－3的点的右边的部分来表示；(2)x≤2可用数轴上表示2的点和它左边的部分来表示．
在数轴上表示不等式的解集时，要确定边界和方向. (1) 边界：有等号的是实心圆点，无等号的是空心圆圈. (2) 方向 ：大于向右，小于向左.
1. 如图，数轴所表示的不等式的解集________.
2.根据数轴上表示的不等式的解集，写出不等式的特殊解：
自然数解：________
负整数解：______
最小的正整数解：______
问题：观察下列不等式：80x>60(x+1)，x>3，m+10≤ m，2x＜x+2.它们有哪些共同点？
这些不等式中都含有几个未知数？那么这些未知数的次数又是几？
我们把含有一个未知数，并且未知数的次数都是1的不等式叫做一元一次不等式.
(1)中未知数的最高次数是2，故不是一元一次不等式；(2)中左边不是整式，故不是一元一次不等式；(3)中有两个未知数，故不是一元一次不等式；(4)是一元一次不等式
下列式子中，是一元一次不等式的有(　　)(1)x2＋1＞2x； (2) ＋2＞0；(3)x＞y； (4) ≤1.A．1个　　B．2个 C．3个 D．4个
例3. 已知 是关于x的一元一次不等式，则a的值是________．
先对所给不等式进行化简整理，再看(1)不等式的左右两边都是整式；(2)不等式中只含有一个未知数；(3)未知数的次数是1.(4)未知数系数不为0.
判断一个不等式是否为一元一次不等式的方法：
判断下列不等式是否为一元一次不等式.（1）3x-2>7 （6）（2）x2≤6 （7）2（1-y）+y＜2y+3（3）x+y≤3y+2 （8）x2-2x+1=0 （4）（5）-2＜3
四、利用不等式的基本性质解一元一次不等式
例4. 解不等式 x+1＜5，并把解集在数轴上表示出来. 解：不等式两边都减去1，得 x＜5-1， 即 x＜4. 两边都乘以（或除以 ），得 x＜8.
解：不等式两边都加上a，得 2x≥ a−3， 两边都除以2，得 x≥ (a−3)， 因为由图可知x≥-1，所以 (a−3) = -1 解得a=1.
例5. 已知关于x的不等式2x-a≥-3的解集如图所示，则a的值等于多少？
方法归纳：(1)先化不等式为x≥m的形式.(2)再与图中的解集比较，列方程求解.(3)注意区别不等式的解和解集，它们是个体和整体的关系.
解不等式－2x＞ ，并把解集在数轴上表示出来.
－2x＞ ，－2x× ＜ × ，得x＜－ .把这个不等式的解集在数轴上表示，如图所示．
1. 下列说法正确的是 （ ）A.x=4是x-30的解C.x=3是x+3≥6的唯一解 D.x