艺考生专题讲义45 抛物线-2024-2025学年高考数学艺体生一轮复习试题

这是一份艺考生专题讲义45 抛物线-2024-2025学年高考数学艺体生一轮复习试题，共8页。试卷主要包含了B．4C．5D．6等内容，欢迎下载使用。
一．抛物线的定义
平面内与一个定点F和一条定直线l(点F不在直线l上)的距离相等的点的轨迹叫做抛物线，定点F叫做抛物线的焦点，定直线l叫做抛物线的准线.
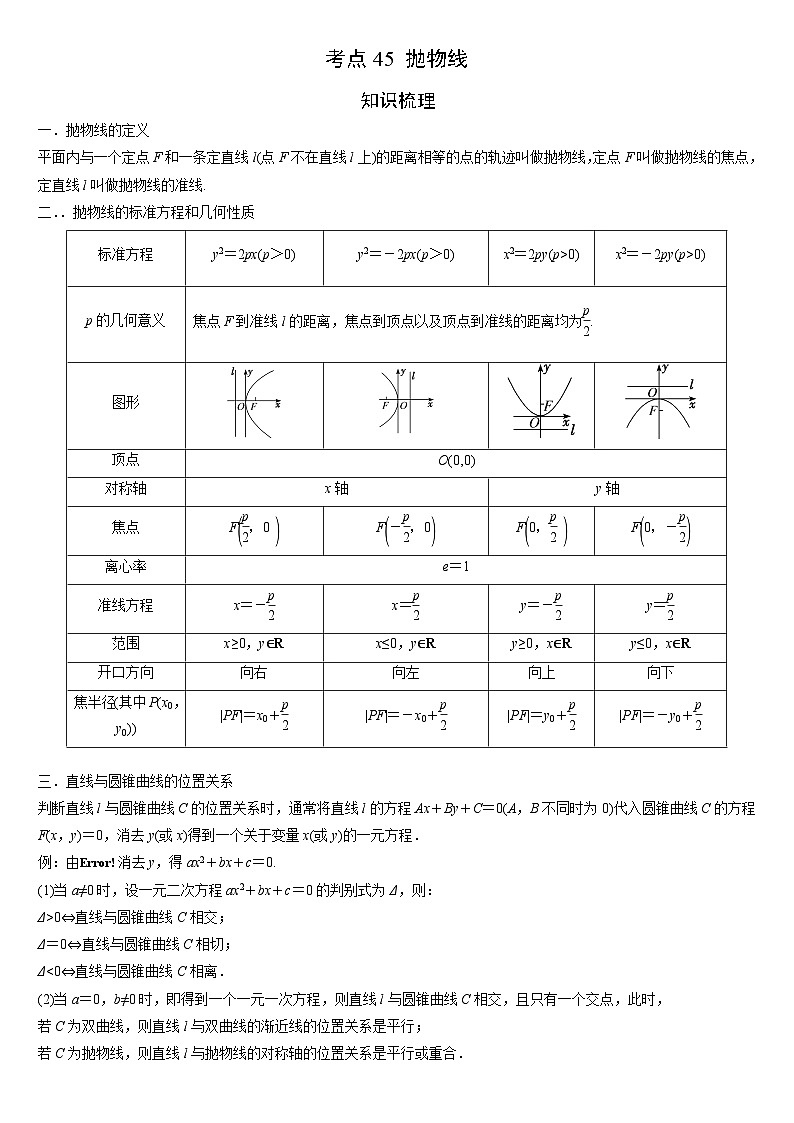
二．．抛物线的标准方程和几何性质
三．直线与圆锥曲线的位置关系
判断直线l与圆锥曲线C的位置关系时，通常将直线l的方程Ax＋By＋C＝0(A，B不同时为0)代入圆锥曲线C的方程F(x，y)＝0，消去y(或x)得到一个关于变量x(或y)的一元方程．
例：由eq \b\lc\{\rc\ (\a\vs4\al\c1(Ax＋By＋C＝0，,Fx，y＝0))消去y，得ax2＋bx＋c＝0.
(1)当a≠0时，设一元二次方程ax2＋bx＋c＝0的判别式为Δ，则：
Δ>0⇔直线与圆锥曲线C相交；
Δ＝0⇔直线与圆锥曲线C相切；
Δ0)，将(－4，5)代入得所以，抛物线方程为．故选：C．
【例2-2】(2024·浙江)已知抛物线的焦点，则拋物线C的标准方程为___________，焦点到准线的距离为___________.
【答案】
【解析】根据抛物线的焦点，设抛物线方程，，则，
故抛物线方程；抛物线中，焦点到准线的距离为，，即距离为.
故答案为：；.
【举一反三】
1．(2024·全国课时练习)以轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8，若抛物线的顶点在坐标原点，则其方程为( )
A．B．
C．或D．或
【答案】C
【解析】设抛物线方程为或，
依题意得，代入或得，
，．
抛物线方程为或，
故选：C.
2．(2024·山东德州市·高二期末)抛物线的焦点是直线与坐标轴的交点，则该抛物线的准线方程是( )
A．B．C．D．
【答案】C
【解析】由可知抛物线开口向上或向下，
，令，焦点坐标为
准线为
故选：C
3．(2024·绵阳南山中学实验学校(文))顶点在原点，对称轴是y轴，并且顶点与焦点的距离等于3的抛物线的标准方程是( )
A．B．
C．D．
【答案】C
【解析】由抛物线的顶点在原点，对称轴是y轴，设抛物线的方程为，
因为顶点与焦点的距离等于，可得，解得，
所以所求抛物线的方程为.
故选：C.
4(2024·广东湛江市·高三一模)已知抛物线C：x2=-2py(p>0)的焦点为F，点M是C上的一点，M到直线y=2p的距离是M到C的准线距离的2倍，且｜MF|=6，则p=( )
A．4B．6C．8D．10
【答案】A
【解析】
设，则，解得
故选：A
题型三 抛物线的几何性质
【例3】(2024·江苏省天一中学高三二模)过抛物线y2＝4x的焦点作直线交抛物线于A(x1，y1)，B(x2，y2)两点，如果x1＋x2＝6，则|AB|＝________．
【答案】8
【解析】抛物线y2＝4x中，，焦点F(1，0)，而直线AB过焦点F(1，0)，
故根据抛物线定义可知.
故答案为：8.
【举一反三】
1．(2024·四川遂宁市·高三二模(文))若过抛物线：的焦点且斜率为2的直线与交于，两点，则线段的长为( )
A．3.B．4C．5D．6
【答案】C
【解析】抛物线：的焦点
所以直线的方程为，
设，，
由，消去并整理得，
所以，.
故选：C.
2．(2024·广西玉林市·高三其他模拟(理))已知抛物线的焦点在直线上，又经过抛物线C的焦点且倾斜角为的直线交抛物线C于A､B两点，则( )
A．12B．14C．16D．18
【答案】C
【解析】因为直线与轴的交点为，
所以抛物线的焦点坐标为，设，抛物线方程为，
所以过焦点且倾斜角为的直线方程为，
设，
由，得，
所以，
所以，
故选：C
3．(2024·商丘市第一高级中学)设F为抛物线的焦点，过F作倾斜角为的直线与该抛物线交于两点，且为坐标原点，则的面积为( )
A．B．C．D．
【答案】A
【解析】由题意得焦点坐标为，则直线的方程为，设，
直线与曲线联立，可得，
，，
又，
解得，又，所以，
所以，
直线方程为，即，
所以原点O到直线的距离，
所以的面积.
故选：A
备战高考数学成套的一轮复习，二轮复习，专题高分突破，考前回归，模拟试卷尽在备战高考QQ群722859698也可联系微信fjshuxue加入夸克网盘群3T一线老师必备资料一键转存自动更新永不过期
标准方程
y2＝2px(p＞0)
y2＝－2px(p＞0)
x2＝2py(p>0)
x2＝－2py(p>0)
p的几何意义
焦点F到准线l的距离，焦点到顶点以及顶点到准线的距离均为eq \a\vs4\al(\f(p,2).)
图形
顶点
O(0,0)
对称轴
x轴
y轴
焦点
Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(p,2)))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，－\f(p,2)))
离心率
e＝1
准线方程
x＝－eq \f(p,2)
x＝eq \f(p,2)
y＝－eq \f(p,2)
y＝eq \f(p,2)
范围
x≥0，y∈R
x≤0，y∈R
y≥0，x∈R
y≤0，x∈R
开口方向
向右
向左
向上
向下
焦半径(其中P(x0，y0))
|PF|＝x0＋eq \f(p,2)
|PF|＝－x0＋eq \f(p,2)
|PF|＝y0＋eq \f(p,2)
|PF|＝－y0＋eq \f(p,2)