艺考生专题讲义01 集合-2024-2025学年高考数学艺体生一轮复习试题

这是一份艺考生专题讲义01 集合-2024-2025学年高考数学艺体生一轮复习试题，共7页。试卷主要包含了集合与元素，已知x∈{1，2，x2}，则有，已知集合，则集合中元素的个数为等内容，欢迎下载使用。
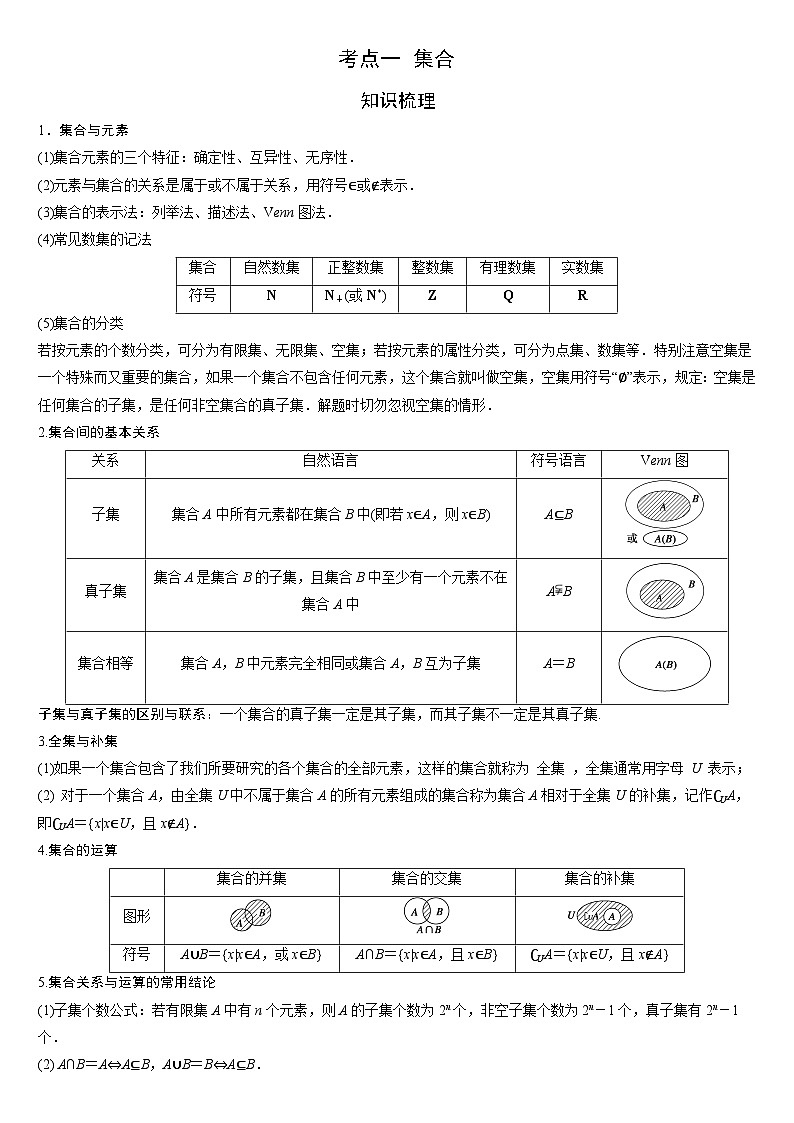
1．集合与元素
(1)集合元素的三个特征：确定性、互异性、无序性．
(2)元素与集合的关系是属于或不属于关系，用符号∈或∉表示．
(3)集合的表示法：列举法、描述法、Venn图法．
(4)常见数集的记法
(5)集合的分类
若按元素的个数分类，可分为有限集、无限集、空集；若按元素的属性分类，可分为点集、数集等．特别注意空集是一个特殊而又重要的集合，如果一个集合不包含任何元素，这个集合就叫做空集，空集用符号“∅”表示，规定：空集是任何集合的子集，是任何非空集合的真子集．解题时切勿忽视空集的情形．
2.集合间的基本关系
子集与真子集的区别与联系：一个集合的真子集一定是其子集，而其子集不一定是其真子集.
3.全集与补集
(1)如果一个集合包含了我们所要研究的各个集合的全部元素，这样的集合就称为 全集 ，全集通常用字母 U 表示；
(2) 对于一个集合A，由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集，记作∁UA，即∁UA＝{x|x∈U，且x∉A}．
4.集合的运算
5.集合关系与运算的常用结论
(1)子集个数公式：若有限集A中有n个元素，则A的子集个数为2n个，非空子集个数为2n－1个，真子集有2n－1个．
(2) A∩B＝A⇔A⊆B，A∪B＝B⇔A⊆B．
(3)(∁UA)∩(∁UB)＝∁U(A∪B)，(∁UA)∪(∁UB)＝∁U(A∩B) ．
题型一 元素的特征
【例1】已知，则实数的值为( )
A．B．C．或 D．无解
【答案】B
【解析】因为，当时，那么，违反集合元素的互异性，不满足题意，当时，，集合为满足题意，实数的值为，故选B.
【举一反三】
1．已知，则实数a的值为( )
A．1或B．1C．D．或0
【答案】C
【解析】当时，得，此时，不满集合中元素的互异性，不合题意；
当时，得，若，则，不满集合中元素的互异性，不合题意；若，则，满足.故选：C
2．(多选)已知x∈{1，2，x2}，则有( )
A．B．C．D．
【答案】BC
【解析】由x∈{1，2，x2}，
当，不满足集合中元素的互异性；
当，满足集合中元素的互异性，符合题意；
当或(舍)，
当满足集合中元素的互异性，符合题意；故选：BC.
3．已知集合，则集合中元素的个数为( )
A．5 B．4 C．3 D．2
【答案】C
【解析】由,得,故.集合中元素的个数为3,选C.
4．已知集合，若，则__________．
【答案】1
【解析】依题意，分别令，，，
由集合的互异性，解得，则.故答案为：
题型二 子集的个数
【例2】已知集合，则集合A的子集个数为( )
A．4B．5C．6D．8
【答案】A
【解析】由，得，得，所以，
因为，所以或，所以，所以集合A的子集个数为.故选：A
【方法总结】
先化简集合，再判断集合中元素的个数，然后代入对应公式
【举一反三】
1．集合的非空子集个数为( )
A．3B．4C．7D．8
【答案】A
【解析】,集合共有个子集，非空子集个数为4-1=3个，
故选：A
2．已知集合，集合，则集合的子集个数为( )
A．2B．4C．6D．8
【答案】D
【解析】∵，，
∴，∴集合的子集个数为8个，故选：D.
3．已知集合，则集合的真子集个数为( )
A．B．C．D．
【答案】A
【解析】，
所以，集合的真子集个数为.故选：A.
4．设集合，，，则M中元素的个数为( )
A．3B．4C．5D．6
【答案】B
【解析】由题意知，则x的可能取值为5,6,7,8.因此集合M共有4个元素，故选B.
题型三 集合间的关系
【例3】(1)已知集合，，若，则实数的取值集合为( )
A．B．C．D．
(2)设集合，，若，则的最大值为( )
A．1B．2C．3D．4
【答案】(1)D(2)B
【解析】(1)∵集合M={x|x2=1}={﹣1，1}，N={x|ax=1}，N⊆M，∴当a=0时，N=∅，成立；
当a≠0时，N={}，∵N⊆M，∴或=1．解得a=﹣1或a=1，
综上，实数a的取值集合为{1，﹣1，0}．故选D．
(2)由题，，∵，∴，∴的最大值为2.故选：B．
【方法总结】
子集求参数时要注意两点
子集有参数时，分子集为空集和非空集
只有里实外空不取等号
【举一反三】
1．已知集合，则下列关系中：①；②；③；④；表述正确的个数为( )
A．1B．2C．3D．4
【答案】D
【解析】集合，则 ；；；表述均正确.故选：.
2．已知集合A＝{﹣1，2}，B＝{x|ax＝1}，若B⊆A，则由实数a的所有可能的取值组成的集合为( )
A．B．C．D．
【答案】D
【解析】当时, ，满足条件，所以，
当时, ，由B⊆A得或，所以或，
因此由实数a的所有可能的取值组成的集合为故选：D
3．(2020·定远县育才学校高三月考(文))已知集合，非空集合，，则实数的取值范围为( ).
A．B．C．D．
【答案】B
【解析】，由且为非空集合可知，
应满足，解得故选：B
题型四 集合间运算
【例4】(1)已知集合P=，，则PQ=( )
A．B．
C．D．
(2)设集合A={x|1≤x≤3}，B={x|2