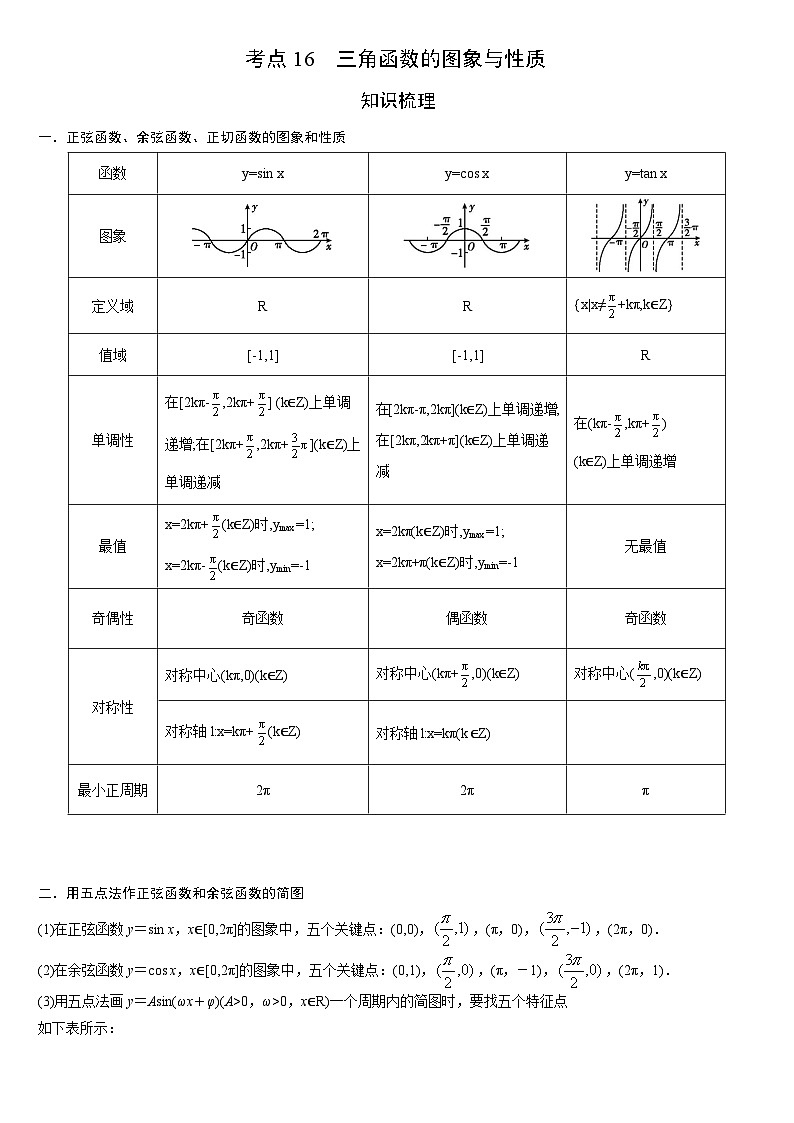
艺考生专题讲义16 三角函数的图象与性质-2024-2025学年高考数学艺体生一轮复习试题

这是一份艺考生专题讲义16 三角函数的图象与性质-2024-2025学年高考数学艺体生一轮复习试题，共15页。
二．用五点法作正弦函数和余弦函数的简图
(1)在正弦函数y＝sin x，x∈[0,2π]的图象中，五个关键点：(0,0)，，(π，0)，，(2π，0)．
(2)在余弦函数y＝cs x，x∈[0,2π]的图象中，五个关键点：(0,1)，，(π，－1)，，(2π，1)．
(3)用五点法画y＝Asin(ωx＋φ)(A>0，ω>0，x∈R)一个周期内的简图时，要找五个特征点
如下表所示：
三．函数y＝sin x的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径
精讲精练
题型一 周期
【例1】下列函数中，最小正周期为的是（ ）.
A．B．C．D．
【答案】C
【解析】由题意知周期为，周期为，周期为，周期为.
【方法总结】
求三角函数最小正周期的常用方法
公式法：将函数化为y＝Asin(ωx＋φ)＋B或y＝Acs(ωx＋φ)＋B的形式，
再利用T＝eq \f(2π,|ω|)求得；y＝Atan(ωx＋φ)＋B,
(2)图象法：利用变换的方法或作出函数的图象，通过观察得到最小正周期.
【举一反三】
1．函数的最小正周期为（ ）
A．B．C．D．
【答案】A
【解析】由，得函数的最小正周期为
2．下列函数的最小正周期为π的是（ ）
A．B．
C．D．
【答案】B
【解析】对于A，函数的最小正周期是，A不符合题意；
对于B，函数的最小正周期是，B符合题意；
对于C，函数的最小正周期是，C不符合题意；
对于D，函数的最小正周期是，D不符合题意.
3．在函数①，②，③，④中，最小正周期为π的函数有（ ）
A．①③B．①④
C．③④D．②③
【答案】D
【解析】①由余弦函数的奇偶性可知，，最小值周期为；
②由翻折变换可知，函数的图象如图：
由图知的最小值周期为；
③由周期公式得，所以的最小值周期为；
④的最小值周期为.
4．函数是（ ）
A．周期为π的奇函数B．周期为π的偶函数
C．周期为2π的奇函数D．周期为2π的偶函数
【答案】D
【解析】因为，所以该函数是周期为2π的偶函数．
题型二 对称性
【例2】已知函数，下列结论中错误的是（ ）
A．的最小正周期为B．的图像关于直线对称
C．在上单调递增D．的值域为 [-1，1]
【答案】C
【分析】根据周期公式的计算即可判断A，代入 ，取最大值，即可判断B,根据整体范围即可验证C,D.
【解析】的最小正周期为,故A正确，当时，，故的图像关于直线对称，B正确，当时，，故C错误，，故D正确.
【方法总结】
【举一反三】
1．函数的一条对称轴是（ ）
A．B．C．D．
【答案】B
【解析】令，可得，令，可得.
所以函数的一条对称轴是.
2．若函数的图像关于轴对称，则的值可能为（ ）
A．B．C．D．
【答案】C
【解析】因为函数的图像关于轴对称，
所以当时，取得最值，
所以，得，
对于A，若，则，解得，不合题意，
对于B，若，则，解得，不合题意，
对于C，若，则，解得，题意，
对于D，若，则，解得，不合题意，
3．函数的图象（ ）
A．关于点对称B．关于点对称
C．关于直线对称D．关于直线对称
【答案】D
【解析】由题设，由余弦函数的对称中心为，令，得，，易知A、B错误；
由余弦函数的对称轴为，令，得，，
当时，，易知C错误，D正确；
4．下列关于函数的说法正确的是（ ）
A．图象关于点成中心对称B．图象关于直线成轴对称
C．在区间上单调递增D．在区间上单调递增
【答案】A
【解析】当时，，所以是函数的中心对称，
所以A选项正确，B选项错误.
C选项，注意到时，，而不存在，所以C选项错误.
D选项，注意到时，，而不存在，所以D选项错误.
题型三 单调性
【例3】函数的单调递增区间是（ ）
A．B．
C．D．
【答案】B
【解析】因为，令，，
解得，，所以函数的单调递增区间为．
【方法总结】
【举一反三】
1．函数在下列哪个区间上单调递增（ ）
A．B．C．D．
【答案】C
【解析】令，，得，令可得，的一个增区间为，结合选项可得C符合题意.
2．下列区间中，函数单调递增的是（ ）
A．B．C．D．
【答案】D
【解析】由，得．
所以在上不单调递增，在上单调递增．
3．已知函数，则（ ）
A．在上单调递减B．在上单调递减
C．在上单调递减D．在上单调递减
【答案】C
【解析】依题意可知，，记，则，
对于A选项，因为，所以，则在上单调递增，故A错误；
对于B选项，因为，所以，则在上不单调，故B错误；
对于C选项，因为，所以，则在上单调递减，故C正确；
对于D选项，因为，所以，则在上不单调，故D错误.
4．若函数在上恰有两个零点，且在上单调递增，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】解：由题意得：
函数在上恰有两个零点，，解得：①，
又在上单调递增，，解得：②，
由①②式联立可知的取值范围是.
故选：B
题型四 奇偶性
【例4】函数是（ ）
A．最小正周期为的偶函数B．最小正周期为的偶函数
C．最小正周期为的奇函数D．最小正周期为的奇函数
【答案】D
【解析】，
由于，且的定义域为全体实数，所以是奇函数，注意到它的周期为.
故选：D.
【方法总结】
【举一反三】
1．下列函数中，是奇函数且最小正周期为1的函数为（ ）
A．B．
C．D．
【答案】B
【解析】对A，其最小正周期为，故A错误；
对B，设，且，解得，
其定义域为，关于原点对称，其最小正周期为，故B正确；
对C，其最小正周期为，故C错误；
对D，设 ，定义域为，关于原点对称，
则，则其为偶函数，故D错误.
故选：B.
2．下列函数中，周期是，又是奇函数的是（ ）
A．B．
C．D．
【答案】D
【解析】对于A.周期是，A错误；
对于B.周期是，因为是偶函数，B错误；
对于C.周期是，因为是偶函数，C错误；
对于D.周期是，又是奇函数，D正确；
故选：D.
3．已知函数是奇函数，则的值可以是（ ）
A．B．C．D．
【答案】D
【解析】是奇函数，则只需，
所以，所以时，.故选：D.
4．函数向左平移个单位得到，若是偶函数，则（ ）
A．B．C．D．
【答案】D
【解析】由题意，
在中，向左平移得到，所以，
因为为偶函数，所以，
又因为，所以，故选：D.
题型五 值域(最值)
【例5】函数的最大值为（ ）
A．B．C．D．0
【答案】C
【解析】由题意可得，
所以的最大值为．
【举一反三】
1．函数的值域为（ ）
A．B．C．D．
【答案】B
【解析】函数，因为，
所以函数的值域为
故选：B.
2．函数的最大值和最小值分别为（ ）
A．B．C．D．
【答案】A
【解析】由，得，则当，即时，，
当，即时，，所以所求最大值、最小值分别为.故选：A
3．若函数的最大值为 ，则a的值等于（ ）
A．2B． C．0D．
【答案】D
【解析】由于，所以时，取最大值，故 ，所以，
4．函数的值域是（ ）
A．B．C．D．
【答案】A
【解析】函数，
∵，∴当时，函数取得最小值为，
当时，函数取得最大值为2，
故函数的值域为，故选：A．
题型六 图象变换
【例6】（1）把函数的图像上所有点的横坐标缩短到原来的，纵坐标伸长到原来的倍，最后把图像向左平移个单位长度，则所得图像表示的函数的解析式为
A．B．C．D．
【答案】B
【解析】把函数的图像上所有点的横坐标缩短到原来的，
所得图像的函数解析式为，再把纵坐标伸长到原来的倍，
所得图像的函数解析式为，最后把图像向左平移个单位长度，
所得图像的函数解析式为.
故选B.
（2）将函数的图象沿轴向左平移个单位后得到函数，若为偶函数，则的最小值为( )
A．B．C．D．
【答案】A
【解析】函数，
将函数的图象沿轴向左平移个单位后，得到函数，
因为函数是偶函数，．当时，．故选：A
【方法总结】
函数图像平移异名化同名的公式：，.
【举一反三】
1．要得到的图像，只需将函数的图像( )
A．向左平移个单位B．向右平移个单位
C．向左平移个单位D．向右平移个单位
【答案】B
【解析】，，
需将函数的图象向右平移个单位.故选：B.
2．将函数的图象向左平移个单位长度后，所得图象对应的函数为( )
A．B．
C．D．
【答案】B
【解析】将函数的图象向左平移个单位长度后，
所得函数解析式为.故选：B.
3．(多选)把函数的图象上各点的横坐标缩短为原来的 (纵坐标不变)，再将图象向右平移个单位长度得到函数g(x)的图象，则下列说法不正确的是( )
A．g(x)在上单调递增 B．g(x)的图象关于对称
C．g(x)的最小正周期为4π D．g(x)的图象关于y轴对称
【答案】BCD
【解析】把函数的图象上各点的横坐标缩短为原来的得到的图象，
再将图象向右平移个单位长度得到函数的图象．
若，则，∴在上单调递增，故A正确，不符合题意；
由知，g(x)的图象不关于点对称，故B错误，符合题意；
g(x)的最小正周期为π，故C错误，符合题意；
∵，∴g(x)的图象不关于y轴对称，故D错误，符合题意．
故选：BCD.
4．将函数的图像向左平移个单位后所得函数图像关于原点中心对称，则_________．
【答案】
【解析】解：根据题意得函数的图像向左平移个单位后得到的函数解析式为：，
由函数图象关于原点中心对称，
故，即所以.故答案为：
题型七 求解析式
【例7】函数的部分图象如图所示，则的单调递增区间为( )
A．，B．，
C．，D．，
【答案】D
【解析】依题意，所以，
由于图象过，所以，
由于，所以，所以.
由得，
所以的单调递增区间为，.故选：D
【方法总结】
由函数的图象求解析式的方法：
（1）；（2）；
（3）； （4）由图象上的已知点求.
【举一反三】
1．数的一段图象如图所示，则( )
A．B．C．D．
【答案】B
【解析】由题意，函数的一段图象，可得，所以，
又由，解得.故选：B.
2．(多选)函数(＞0，0＜＜)(xR)在一个周期内的图象如图所示，则( )
A．函数的解析式为(xR)
B．函数的一条对称轴方程是
C．函数的对称中心是(，0)，kZ
D．函数是偶函数
【答案】BD
【解析】对于选项，由图象可知周期为，所以，
由图象过，则，解得，
又0＜＜，则，
所以函数.所以A选项不正确；
对于B选项，当时，，为最小值，所以选项B正确；
对于C选项，当时，，显然对称中心不是(，0)，故选项C错误；
对于D选项，，为偶函数，故选项D正确.故选：BD.
3．(多选）已知函数的部分图象如图所示，则下列说法正确的是( )
A．最小正周期为
B．在区间上单调递增
C．的图象关于点对称
D．的图象可由的图象向在平移个单位长度得到
【答案】BC
【解析】由图象可知，，，故的最小正周期为，故A错误；
所以，得.
又因为当时，，即，
即.又因为，可得，解得，
所以.由，
可得，令，可得在区间上单调递增，故B正确；
又，所以的图象关于点对称，故C正确；
的图象向左平移个单位长度得到，故D错误.故选：
备战高考数学成套的一轮复习，二轮复习，专题高分突破，考前回归，模拟试卷尽在备战高考QQ群722859698也可联系微信fjshuxue加入夸克网盘群3T一线老师必备资料一键转存自动更新永不过期
函数
y=sin x
y=cs x
y=tan x
图象
定义域
R
R
{x|x≠ QUOTE +kπ,k∈Z}
值域
[-1,1]
[-1,1]
R
单调性
在[2kπ-,2kπ+] (k∈Z)上单调递增;在[2kπ+,2kπ+] QUOTE (k∈Z)上单调递减
在[2kπ-π,2kπ](k∈Z)上单调递增;在[2kπ,2kπ+π](k∈Z)上单调递减
在(kπ-,kπ+) QUOTE
(k∈Z)上单调递增
最值
x=2kπ+ QUOTE (k∈Z)时,ymax=1;
x=2kπ- QUOTE (k∈Z)时,ymin=-1
x=2kπ(k∈Z)时,ymax=1;
x=2kπ+π(k∈Z)时,ymin=-1
无最值
奇偶性
奇函数
偶函数
奇函数
对称性
对称中心(kπ,0)(k∈Z)
对称中心(kπ+,0)(k∈Z)
对称中心(,0) QUOTE (k∈Z)
对称轴l:x=kπ+ QUOTE (k∈Z)
对称轴l:x=kπ(k∈Z)
最小正周期
2π
2π
π
x
eq \f(0－φ,ω)
eq \f(\f(π,2)－φ,ω)
eq \f(π－φ,ω)
eq \f(\f(3π,2)－φ,ω)
eq \f(2π－φ,ω)
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
y＝Asin(ωx＋φ)
0
A
0
－A
0