数学七年级下册（2024）第八章 整式的乘法8.5 乘法公式示范课ppt课件

这是一份数学七年级下册（2024）第八章 整式的乘法8.5 乘法公式示范课ppt课件，文件包含85第1课时平方差公式pptx、85乘法公式doc等2份课件配套教学资源，其中PPT共34页， 欢迎下载使用。
1.掌握平方差公式的结构特点推导和应用（重点）2.能够应用平方差公式进行简单计算（难点）
计算下列多项式的积,并观察算式和结果的特征 。 (1)( x + 1 )( x – 1) = _______(2)( m - 2 )( m + 2 ) = _______( 3)(2x + 1 )( 2x – 1 ) = ______
规律:两个数的和与这两个数的差的乘积等于相同项的平方减去相反项的平方.
观察如果用字母a、b表示等式左边,能否得出以上规律？
(a+b)(a－b) =
a2－ ab+ab－ b2
(a+b)(a－b)=
(a+b)(a－b)
(a+b)(a−b)=
两数和与这两数差的积,等于这两数的平方差.
1.（a – b ) ( a + b) = a2 - b2
2.（b + a )( -b + a ) = a2 - b2
注：这里的两数可以是两个单项式也可以是两个多项式等．
(a+b)(a-b)=(a)2-(b)2
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
( 0.3x)2-12
练一练：口答下列各题： (l)(-a+b)(a+b)=_________. (2)(a-b)(b+a)= __________. (3)(-a-b)(-a+b)= ________. (4)(a-b)(-a-b)= _________.
计算时注意：一定要把要计算的式子与公式对照，找出哪个是a ，哪个是b.
在区分a，b时：如果字母前面有负号的，同号为a，异号为b。
应用平方差公式计算时，应注意以下几个问题：(1)左边是两个二项式相乘，并且这两个二项式中有 一项完全相同，另一项互为相反数；(2)右边是相同项的平方减去相反项的平方；(3)公式中的a和b可以是具体数，也可以是单项式或 多项式．
利用平方差公式计算：(1)(3x－5)(3x＋5)； (2)(－2a－b)(b－2a)；(3)(－7m＋8n)(－8n－7m)．
解：(1)原式=(3x)2－52＝9x2－25；
(2)原式=(－2a)2－b2＝4a2－b2；
(3)原式=(－7m)2－(8n)2＝49m2－64n2；
【例2】计算:(1) 102×98;(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 102×98
（2）(y+2)(y-2)- (y-1)(y+5)
=10000 – 4
=（100＋2）(100－2)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
计算:(1) 51×49; (2)(3x+4)(3x-4)-(2x+3)(3x-2) .
解: (1) 原式=（50＋1）(50－1)
(2) 原式=(3x)2-42-(6x2+5x-6)
= 9x2-16-6x2-5x+6
= 3x2-5x-10.
【例3】先化简，再求值：(2x－y)(y＋2x)－(2y＋x)(2y－x)，其中x＝1，y＝2.
原式＝5×12－5×22＝－15.
解：原式＝4x2－y2－(4y2－x2)
＝4x2－y2－4y2＋x2
【例4】对于任意的正整数n，整式(3n＋1)(3n－1)－(3－n)(3＋n)的值一定是10的整数倍吗？
即(3n＋1)(3n－1)－(3－n)(3＋n)的值是10的倍数．
解：原式＝9n2－1－(9－n2)
∵(10n2－10)÷10=n2-1.
对于平方差中的a和b可以是具体的数，也可以是单项式或多项式，在探究整除性或倍数问题时，一般先将代数式化为最简，然后根据结果的特征，判断其是否具有整除性或倍数关系．
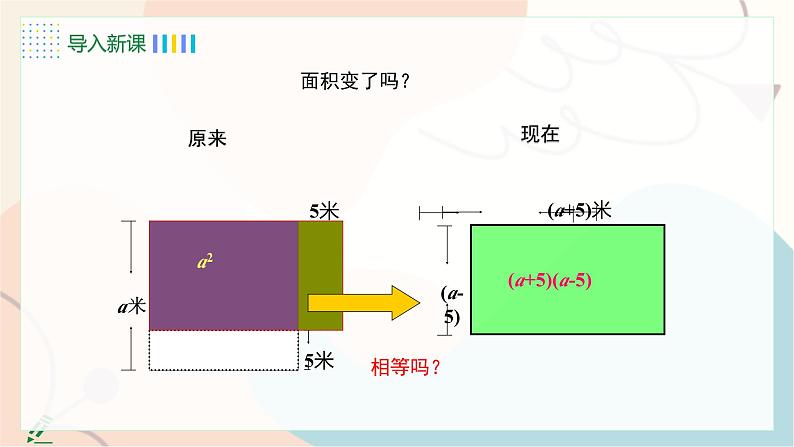
【例5】王大伯家把一块边长为a米的正方形土地租给了邻居李大妈．今年王大伯对李大妈说：“我把这块地一边减少4米，另外一边增加4米，继续租给你，你看如何？”李大妈一听，就答应了．你认为李大妈吃亏了吗？为什么？
理由：原正方形的面积为a2，
改变边长后面积为(a＋4)(a－4)＝a2－16，
解决实际问题的关键是根据题意列出算式，然后根据公式化简算式，解决问题．
1.下列运算中，可用平方差公式计算的是(　　) A．(x＋y)(x＋y) B．(－x＋y)(x－y) C．(－x－y)(y－x) D．(x＋y)(－x－y)
2.计算（2x+1）（2x-1）等于（　　） A．4x2-1 B．2x2-1 C．4x-1 D．4x2+1
3.下列运算正确的是(　　) A．(a－2b)(a－2b)＝a2－4b2 B．(－a＋2b)(a－2b)＝－a2＋4b2 C．(a＋2b)(－a＋2b)＝a2－4b2 D．(－a－2b)(－a＋2b)＝a2－4b2
4. 两个正方形的边长之和为5，边长之差为2，那么用较大的正方形的面积减去较小的正方形的面积，差是________．
（1）(a+3b)(a- 3b)；
原式=(2a+3)(2a-3)
原式=(-2x2 )2－y2
原式=(a)2－(3b)2
（2）(3+2a)(－3+2a)；
（3）(－2x2－y)(－2x2+y).
5. 利用平方差公式计算：
6. 计算： 20202 － 2019×2021.
20202 － 2019×2021
= 20202 － (2020－1)(2020+1)
－ （20202－12 )
7. 利用平方差公式计算:
（1）（a-2)(a+2)(a2 + 4) 解:原式=(a2-4)(a2+4) =a4-16.
(2) (x-y)(x+y)(x2+y2)(x4+y4).
解：原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
8. 先化简，再求值：(x＋1)(x－1)＋x2(1－x)＋x3，其中x＝2.
解：原式=x2－1＋x2－x3＋x3
原式=2×22－1=7.
9. 已知x≠1，计算：(1＋x)(1－x)＝1－x2，(1－x)(1＋x＋x2)＝1－x3，(1－x)(1＋x＋x2＋x3)＝(1)观察以上各式并猜想：(1－x)(1＋x＋x2＋…＋xn)＝________；(n为正整数)
(2)根据你的猜想计算：①(1－2)(1＋2＋22＋23＋24＋25)＝________；②2＋22＋23＋…＋2n＝________(n为正整数)；③(x－1)(x99＋x98＋x97＋…＋x2＋x＋1)＝________；
(3)通过以上规律请你进行下面的探索：①(a－b)(a＋b)＝________；②(a－b)(a2＋ab＋b2)＝________；③(a－b)(a3＋a2b＋ab2＋b3)＝________．