









所属成套资源:2025年高考数学二轮复习课件(含练习)
专题二 微创新 解三角形与其他知识的综合问题 -2025年高考数学二轮复习课件(含练习)
展开
这是一份专题二 微创新 解三角形与其他知识的综合问题 -2025年高考数学二轮复习课件(含练习),文件包含专题二微创新解三角形与其他知识的综合问题pptx、专题二微创新解三角形与其他知识的综合问题docx等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
随着高考改革的不断推进,各地的模拟题呈现的考查方向百花齐放,以三角形为背景,其考查的知识内容和范围,涉及平面几何、立体几何、不等式、向量、新定义等学科分支,对综合运用各种知识技能解题的灵活性要求有所加强,应予以重视.
解三角形与其他知识的交汇
解三角形中的新定义、新情境问题
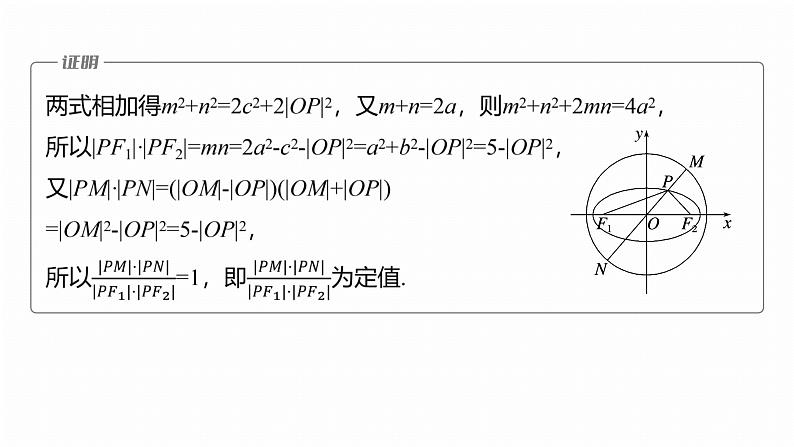
[蒙日圆]在圆x2+y2=4上任取一点T,过点T作x轴的垂线段TD,垂足为D.当点T在圆上运动时,线段TD的中点Q的轨迹是椭圆C(当点T经过圆与x轴的交点时,规定点Q与点T重合).(1)求该椭圆C的方程;
解三角形与立体几何、解析几何结合,利用正弦定理、余弦定理可以将几何体中的长度、角度联系在一起,可以考查几何体中的线段长度或者几何体中的角度之间的关系,或者构造长度、角度的函数求最值问题.
(2024·重庆模拟)“费马问题”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当△ABC的三个内角均小于120°时,使得∠AOB=∠BOC=∠COA=120°的点O即为费马点;当△ABC有一个内角大于或等于120°时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知△ABC的内角A,B,C所对的边分别为a,b,c,且cs 2B+cs 2C-cs 2A=1.(1)求A;
(3)设点P为△ABC的费马点,|PB|+|PC|=t|PA|,求实数t的最小值.
通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情境,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使问题得以解决.
(2024·宿迁模拟)法国著名军事家拿破仑·波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边,向外构造三个等边三角形,则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点.”如图,在△ABC中,内角A,B,C的对边分别为a,b,c,已知2ccs A-acs B=bcs A.以AB,BC,AC为边向外作三个等边三角形,其外接圆圆心依次为O1,O2,O3,连接O1O2,O2O3,O1O3,得到△O1O2O3. (1)求A;
(2)若M1,M2,M3,…,Mn-1是△ABC的边BC的n(n≥2)等分点,由A对BC施以视角运算,证明:(B,C;Mk)×(B,C;Mn-k)=1(k=1,2,3,…,n-1).
相关课件
这是一份专题二 微专题2 解三角形 -2025年高考数学二轮复习课件(含练习),文件包含专题二微专题2解三角形pptx、专题二微专题2解三角形docx等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
这是一份专题五 微创新 概率、统计与其他知识的综合问题--2025年高考数学大二轮复习课件+讲义+专练,文件包含专题五微创新概率统计与其他知识的综合问题--2025年高考数学大二轮专题复习课件pptx、专题五微创新概率统计与其他知识的综合问题--2025年高考数学大二轮专题复习强化练习docx、专题五微创新概率统计与其他知识的综合问题--2025年高考数学大二轮专题复习教师版docx、专题五微创新概率统计与其他知识的综合问题--2025年高考数学大二轮专题复习学生版docx等4份课件配套教学资源,其中PPT共49页, 欢迎下载使用。
这是一份专题四 微创新 立体几何与其他知识的综合问题--2025年高考数学大二轮复习课件+讲义+专练,文件包含专题四微创新立体几何与其他知识的综合问题--2025年高考数学大二轮专题复习课件pptx、专题四微创新立体几何与其他知识的综合问题--2025年高考数学大二轮专题复习强化练习docx、专题四微创新立体几何与其他知识的综合问题--2025年高考数学大二轮专题复习教师版docx、专题四微创新立体几何与其他知识的综合问题--2025年高考数学大二轮专题复习学生版docx等4份课件配套教学资源,其中PPT共60页, 欢迎下载使用。









