新高考数学一轮复习基础+提升训练专题5.3 平面向量与其它知识的综合应用（2份，原卷版+解析版）

这是一份新高考数学一轮复习基础+提升训练专题5.3 平面向量与其它知识的综合应用（2份，原卷版+解析版），文件包含新高考数学一轮复习基础+提升训练专题53平面向量与其它知识的综合应用原卷版doc、新高考数学一轮复习基础+提升训练专题53平面向量与其它知识的综合应用解析版doc等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

【811】．（2016·四川·高考真题·★★★★）
在平面内，定点A，B，C，D满足==,===–2，动点P，M满足=1，=，则的最大值是
A．B．C．D．
【答案】B
【解析】
【详解】
试题分析：甴已知易得.以为原点，直线为轴建立平面直角坐标系，如图所示，则设由已知，得，又
，它表示圆上的点与点的距离的平方的，，故选B.
【考点】平面向量的数量积运算，向量的夹角，解析几何中与圆有关的最值问题
【名师点睛】本题考查平面向量的夹角与向量的模，由于结论是要求向量模的平方的最大值，因此我们要把它用一个参数表示出来，解题时首先对条件进行化简变形，本题中得出，且，因此我们采用解析法，即建立直角坐标系，写出点的坐标，同时动点的轨迹是圆，则，因此可用圆的性质得出最值．因此本题又考查了数形结合的数学思想．
【812】．（2018·全国·专题练习·★★★★）
在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若= +，则+的最大值为
A．3B．2C．D．2
【答案】A
【解析】
【详解】
如图所示，建立平面直角坐标系.
设,
易得圆的半径，即圆C的方程是，
，若满足，
则 ，，所以，
设，即，点在圆上，
所以圆心到直线的距离，即，解得，
所以的最大值是3，即的最大值是3，故选A.
【名师点睛】（1）应用平面向量基本定理表示向量是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.
（2）用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决.
【813】．（2013·湖南·高考真题·★★★）
已知是单位向量，.若向量满足（ ）
A．B．
C．D．
【答案】A
【解析】
【详解】
因为，，做出图形可知，当且仅当与方向相反且时，取到最大值；最大值为；当且仅当与方向相同且时，取到最小值；最小值为.
【814】．（2015·湖南·高考真题·★★★）
已知点A,B,C在圆上运动，且ABBC，若点P的坐标为（2，0），则 的最大值为
A．6B．7C．8D．9
【答案】B
【解析】
【详解】
由题意，AC为直径，所以 ,当且仅当点B为（-1，0）时，取得最大值7，故选B.
考点：直线与圆的位置关系、平面向量的运算性质
【名师点睛】与圆有关的最值问题是命题的热点内容，它着重考查数形结合与转化思想. 由平面几何知识知，圆上的一点与圆外一定点距离最值在定点和圆心连线与圆的两个交点处取到．圆周角为直角的弦为圆的半径，平面向量加法几何意义这些小结论是转化问题的关键.
【815】．（2012·全国·高考真题·★★）
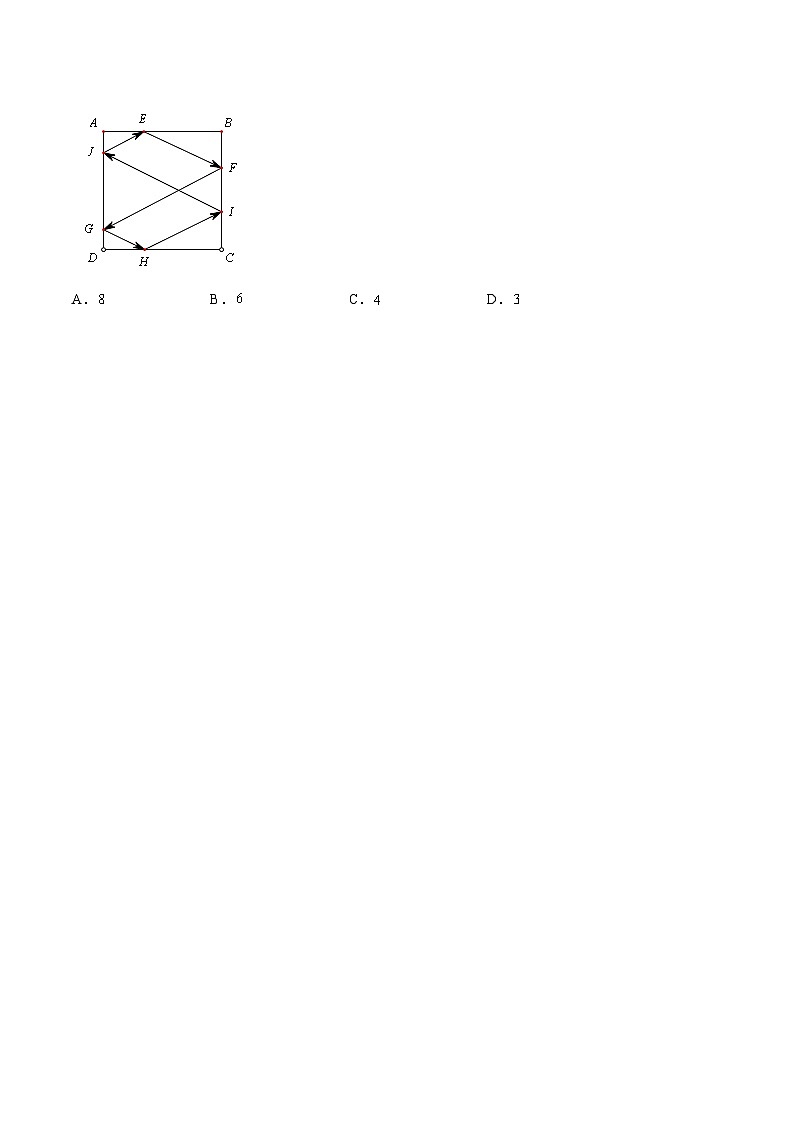
正方形的边长为，点在边上，点在边上，．动点从出发沿直线向运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点第一次碰到时，与正方形的边碰撞的次数为
A．B．C．D．
【答案】B
【解析】
【详解】
结合已知中的点E,F的位置，进行作图，推理可知，在反射的过程中，直线是平行的，那么利用平行关系，作图，可以得到回到EA点时，需要碰撞6次即可.
【816】．（2022·辽宁·鞍山一中模拟预测·★★★★）（多选题）
已知点在所在的平面内，则下列命题正确的是（ ）
A．若为的垂心，，则
B．若为边长为2的正三角形，则的最小值为-1
C．若为锐角三角形且外心为，且，则
D．若，则动点的轨迹经过的外心
【答案】ACD
【解析】
【分析】
A利用三角形相似及数量积的几何意义判断：B构建直角坐标系，由向量数量积的坐标表示列式求最值；C由已知得，进而可知与中点共线，结合外心的性质有垂直平分即可判断；D将等式两侧同时点乘并化简得，即可判断.
【详解】
A：如下图，，则为垂心，易知：，
所以，则，
根据向量数量积的几何意义知：，同理，
所以，正确；
B：构建以中点为原点的直角坐标系，则，若，
所以，，
由，则，
当时的最小值为，错误；

C：由题设，则，
所以，若为中点，则，
故，故共线，又，即垂直平分，
所以，正确；
D：由题设，，
则，
所以，若为中点，则，
故，所以的轨迹经过的外心，正确.
故选：ACD
【点睛】
关键点点睛：A根据垂心性质，三角形相似关系、数量积的几何意义得到；B构建直角坐标系，应用数量积的坐标表示列式判断；C、D根据外心的性质，应用数形结合化简题设向量的线性关系式判断.
【817】．（2022·重庆八中模拟预测·★★★★）（多选题）
在△中，内角所对的边分别为a、b、c，则下列说法正确的是（ ）
A．
B．若，则
C．
D．若，且，则△为等边三角形
【答案】ACD
【解析】
【分析】
A由正弦定理及等比的性质可说明；B令可得反例；C由和角正弦公式及三角形内角和的性质有，由正弦定理即可证；D若，，根据单位向量的定义，向量加法的几何意义及垂直表示、数量积的定义易知△的形状.
【详解】
A：由，根据等比的性质有，正确；
B：当时，有，错误；
C：，而，即，由正弦定理易得，正确；
D：如下图，是单位向量，则，即、，则且平分，的夹角为， 易知△为等边三角形，正确.
故选：ACD
【点睛】
关键点点睛：D选项，注意应用向量在几何图形中所代表的线段，结合向量加法、数量积的几何意义判断夹角、线段间的位置关系，说明三角形的形状.
【818】．（2021·山东泰安·模拟预测·★★★★）（多选题）
如图，在直角三角形中，，点在以为圆心且与边相切的圆上，则（ ）
A．点所在圆的半径为2B．点所在圆的半径为1
C．的最大值为14D．的最大值为16
【答案】AC
【解析】
【分析】
斜边BC上的高即为圆的半径；把求的最大值通过向量加法的三角形法则转化为求的最大值，从而判断出P，M，A三点共线，且P，M在点A的两侧时取最大值.
【详解】
设AB 的中点为M，过A作AH垂直BC于点H，因为，所以，，
所以由，得，所以圆的半径为2，即点所在圆的半径为2，所以选项A正确，B错误；
因为，，，
所以
，
所以当P，M，A三点共线，且P，M在点A的两侧时，取最大值，且最大值为，
所以的最大值为，所以选项C正确，D错误.
故选：AC.
【819】．（2021·广东·珠海市第二中学模拟预测·★★★★）（多选题）
点O在所在的平面内,则以下说法正确的有
A．若,则点O为的重心
B．若,则点O为的垂心
C．若,则点O为的外心
D．若,则点O为的内心
【答案】AC
【解析】
逐项进行分析即可.
【详解】
解：选项A，设D为的中点，由于，所以为边上中线的三等分点(靠近点D)，所以O为的重心；
选项B，向量分别表示在边和上的单位向量，设为和，则它们的差是向量，则当，即时，点O在的平分线上，同理由，知点O在的平分线上，故O为的内心；
选项C，是以为邻边的平行四边形的一条对角线，而是该平行四边形的另一条对角线，表示这个平行四边形是菱形，即，同理有，于是O为的外心；
选项D，由得，
∴，即，
∴．同理可证，
∴，，，即点O是的垂心；
故选：AC．
【点睛】
本题主要考查平面向量在三角形中的应用，考查向量的数量积，考查三角形的“五心”，属于中档题．
【820】．（2022·黑龙江·哈九中二模·★★★）
窗的运用是中式园林设计的重要组成部分，在表现方式上常常运用象征、隐喻、借景等手法，将民族文化与哲理融入其中，营造出广阔的审美意境．从窗的外形看，常见的有圆形、菱形、正六边形、正八边形等．已知圆O是某窗的平面图，O为圆心，点A在圆O的圆周上，点P是圆O内部一点，若，且，则的最小值是（ ）
A．3B．4C．9D．16
【答案】A
【解析】
【分析】
利用向量的线性运算，结合数量积，可求得，确定其取值范围，再根据平方后的式子，即可求得答案.
【详解】
因为，所以，
所以，即，则．
因为点P是圆O内部一点，所以，所以，
则，
当且仅当时，等号成立，故的最小值是3,
故选：A.
【821】．（2020·山西·太原五中二模·★★★）
设O是平面上一定点，A，B，C是平面上不共线的三点，动点P满足，，则点P的轨迹经过的（ ）
A．内心B．外心C．垂心D．重心
【答案】C
【解析】
【分析】
由得出，结合三角形的性质得出答案.
【详解】
则，即，故
即点P的轨迹经过的垂心
故选：C
【822】．（2021·吉林吉林·三模·★★★）
已知､为平面上的两个定点，且，该平面上的动线段的端点､，满足，，，则动线段所形成图形的面积为（ ）
A．36B．60C．72D．108
【答案】B
【解析】
【分析】
根据题意建立平面直角坐标系，根据和，得到动点在直线上，且，进而得到扫过的三角形的面积，再由，同理得到扫过的三角形的面积，两者求和即可.
【详解】
根据题意建立平面直角坐标系，如图所示：
则，，设，
∴，；
由，得；
又，
∴，；
∴；
∴，
∴动点在直线上，且，即线段CD上，则,
则扫过的三角形的面积为，
设点
∵，
∴，
∴，，
∴动点在直线上，且，即线段MN上，则,
∴扫过的三角形的面积为，
∴因此和为60，
故选：B.
【点睛】
关键点点睛：本题关键是由和，得到动点的轨迹，进而得到扫过的三角形的面积而得解.
【823】．（2022·浙江·高考真题·★★★★）
设点P在单位圆的内接正八边形的边上，则的取值范围是_______．
【答案】
【解析】
【分析】
根据正八边形的结构特征，分别以圆心为原点，所在直线为轴，所在直线为轴建立平面直角坐标系，即可求出各顶点的坐标，设，再根据平面向量模的坐标计算公式即可得到，然后利用即可解出．
【详解】
以圆心为原点，所在直线为轴，所在直线为轴建立平面直角坐标系，如图所示：
则,，设,于是，
因为，所以，故的取值范围是.
故答案为：．
【824】．（2015·天津·高考真题·★★★★★）
在等腰梯形 中,已知 ,动点 和 分别在线段 和 上,且, 则的最小值为_____________________.
【答案】
【解析】
【详解】
因为，，
，，
当且仅当即时的最小值为.
考点：向量的几何运算、向量的数量积与基本不等式.
【825】．（2014·江苏·高考真题·★★★）
如图在平行四边形中，已知，，则的值是______．
【答案】22
【解析】
【详解】
由题意，，，
所以，
即，解得．
【考点】向量的线性运算与数量积．
【826】．（2022·北京·人大附中模拟预测·★★★★）
窗花是贴在窗纸或窗户玻璃上的剪纸，是中国古老的传统民间艺术．图1是一张由卷曲纹和回纹构成的正六边形前纸窗花．图2中正六边形的边长为4，圆的圆心为该正六边形的中心，圆的半径为2，圆的直径，点在正六边形的边上运动，则的最小值为（ ）
A．5B．6C．7D．8
【答案】D
【解析】
【分析】
计算得出，求出的取值范围，由此可求得的取值范围，从而可得最小值.
【详解】
如下图所示，由正六边形的几何性质可知，、、、、、均为边长为的等边三角形，
当点位于正六边形的顶点时，取最大值，
当点为正六边形各边的中点时，取最小值，即，
所以，.
所以，.
的最小值为.
故选：D.
【点睛】
方法点睛：求两个向量的数量积有三种方法：
（1）利用定义：
（2）利用向量的坐标运算；
（3）利用数量积的几何意义．
具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．
【827】．（2022·全国·模拟预测·★★★★）
已知H为的垂心，若，则（ ）
A．B．
C．D．
【答案】C
【解析】
【分析】
，，利用、得，，解得， 再利用平方共线可得答案.
【详解】
依题意，，同理．
由H为△ABC的垂心，得，即，
可知，即．同理有，
即，可知，
即，解得，
，又，
所以．
故选：C．
【828】．（2022·山东·胜利一中模拟预测·★★★）
已知为单位向量，满足，则的最小值为（ ）
A．B．C．D．
【答案】A
【解析】
【分析】
设，以为原点建立直角坐标系，设，，可得.
【详解】
设，则，所以为等边三角形，
以为原点建立如图所示直角坐标系，则，
设，，则，
所以在以为圆心，1为半径的圆上，
因为，
所以.
故选：A.
【829】．（2022·重庆八中模拟预测·★★★）
中，，，，PQ为内切圆的一条直径，M为边上的动点，则的取值范围为（ ）
A．B．C．D．
【答案】C
【解析】
【分析】
易知是直角三角形，利用等面积法可得内切圆半径，设内切圆圆心为，根据为直径，可知，，整理，进而根据的运动情况来求解.
【详解】
由题可知，，所以是直角三角形，，
设内切圆半径为，则，解得，
设内切圆圆心为，因为是内切圆的一条直径，
所以，，
则，，
所以，
因为M为边上的动点，所以；当与重合时，，
所以的取值范围是，
故选：C
【830】．（2022·浙江宁波·二模·★★★★★）
已知平面向量，，满足，，，（，）.当时，（ ）
A．B．C．D．
【答案】A
【解析】
【分析】
分析题目条件，得到，画出草图，利用等和线得到，过O点,C点分别向AB做垂线，得到两个相似比为1比3的直角三角形，设出∠CAB=θ，然后利用角表示边，通过勾股定理得到角的大小，从而得到边长的大小，进而求出的大小
【详解】
解析：作，，，由题意，
设直线与直线交于点，
∵（，），
∴点在线段上（不含端点）
又，结合等和线性质，可知
作于，于，
有，
记
①当点在线段上时，，
由，得，可解得，进而有
此时，，
（注：点为线段的中点，在线段上，符合题意）
可得，所以
②当点在线段的反向延长线上时，同①方法可推得点与点重合，矛盾综上，.
故选：A
【831】．（2022·浙江台州·二模·★★★★★）
已知平面向量.若对区间内的三个任意的实数,都有,则向量与夹角的最大值的余弦值为（ ）
A．B．C．D．
【答案】A
【解析】
【分析】
建立直角坐标系,设出相关向量,通过分析位置,寻求临界值.
【详解】
设.
如图,不妨设.
设为AB的中点,为OC的中点,为BD的中点,为AD的中点.
则.
,点在平行四边形内(含边界).
由题知恒成立.
为了使最大,则思考为钝角,即思考点在第一或第四象限.
思考临界值即与重合,与重合,且GM不能充当直角三角形斜边,否则可以改变的位置，使得
所以,即
即,即.
所以.
所以
所以向量与夹角的最大值的余弦值为
故选:A.
【点睛】
关键点点睛：解决本题的关键是利用已知条件转化出所在的位置.
【832】．（2022·上海金山·二模·★★★）
已知平面向量满足，若关于的方程有实数解，则面积的最大值为__________.
【答案】
【解析】
【分析】
对两边平方有有解，再利用基本不等式可得，进而求得面积的最大值即可
【详解】
设，因为，故，则，显然，对两边平方有，即有解，因为，当且仅当，即时取等号.故 ，则面积的最大值为，当且仅当时取等号.
故答案为：
【833】．（2022·浙江·模拟预测·★★★）
已知平面内两单位向量，若满足，则的最小值是___________.
【答案】
【解析】
【分析】
设出得到，由不得关系得到，从而得到最小值.
【详解】
由题意,可以设，
则由得，
由，
所以，解得：
即的最小值是.
【点睛】
对于向量相关的不等式，最值问题，合理设出向量的坐标，可以大大简化做题难度和计算量.
【834】．（2022·江苏盐城·三模·★★★）
已知平面凸四边形ABCD，点E、F分别在AD、BC上，满足，，且，与的夹角为，设，，则的最大值为__________．
【答案】
【解析】
【分析】
以、为基底表示出，再将式子两边平方转化为长度关系，由此即可利用基本不等式求得m+2n的最大值﹒
【详解】
∵①，且②，
则①×2+②得：，
即，
∵，，∴，
两边平方可得，，
∴，解得，
当且仅当时，等号成立．
故答案为：．
【835】．（2022·浙江金华·三模·★★★★）
已知平面向量，，满足，当取到最小值吋，对任意实数，的最小值是___________．
【答案】##
【解析】
【分析】
构造单位圆，设出向量，，，由题设得到CA、CB是圆O的两条切线，，从而由当取到最小值时，求得，结合表示的是以O为起点，终点在AB上的向量，可求得答案.
【详解】
如图，设为单位圆O的两条半径，记，，，
设，由题意，
可知CA、CB是圆O的两条切线，则 ，
故，
当且仅当，即时取“＝”，此时 ，
因为表示的是以O为起点，终点在AB上的向量，
故当该向量垂直于向量 时，其模最小，
记，则 ，则，
故答案为：
【836】．（2022·天津市第四中学模拟预测·★★★★★）
如图，已知，是直角两边上的动点，，，，，，则的最大值为___________.
【答案】
【解析】
【分析】
以点为原点，，所在直线为轴，轴建立平面直角坐标系，设，利用三角函数关系表示，，的坐标，由题干条件分析可知为的中点，为的中点，即可得到，的坐标，进而得到与，整理可得为关于的函数，利用正弦型函数的性质即可求得最大值.
【详解】
如图，以点为原点，，所在直线为轴，轴建立平面直角坐标系，
设，则，，
在中，，，
所以设，，，即.
由题意可知为的中点，为的中点，
所以，，
所以，，
所以

（其中，为锐角），
所以的最大值为，此时，即，
故答案为：
【点睛】
关键点点睛：题目中给出垂直关系，可利用坐标法处理此题，设，点坐标即可用关于的三角函数关系表示，则将问题整理为关于的正弦型函数求最大值问题.
【837】．（2022·四川达州·二模·★★）
在中，为重心，，，则___________.
【答案】
【解析】
【分析】
设中点为，由重心性质知，利用数量积定义可求得，将所求量化为，由数量积的定义和运算律可求得结果.
【详解】
设中点为，
为的重心且，，
，
，
，
.
故答案为：.
【838】．（2022·辽宁·一模·★★★）
已知向量、、，且，，，，则的最小值为______．
【答案】##
【解析】
【分析】
根据题意，建立直角坐标系，写出、、坐标，求出终点轨迹，数形结合即可求解.
【详解】
不妨设，，，
，则起点在原点，终点轨迹为单位圆，
∴当与同向时，最小，为.
故答案为：.