

数学八年级下册第十八章 平行四边形18.1 平行四边形18.1.1 平行四边形的性质教案配套课件ppt
展开观察这些图片,它们都有哪种图形的形象?
你还记得平行四边形的定义吗?
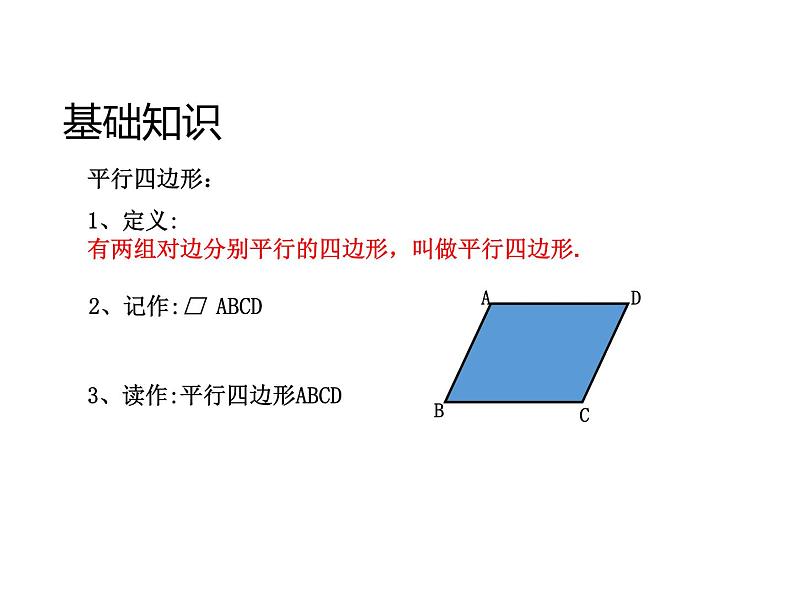
平行四边形:1、定义:有两组对边分别平行的四边形,叫做平行四边形.
3、读作:平行四边形ABCD
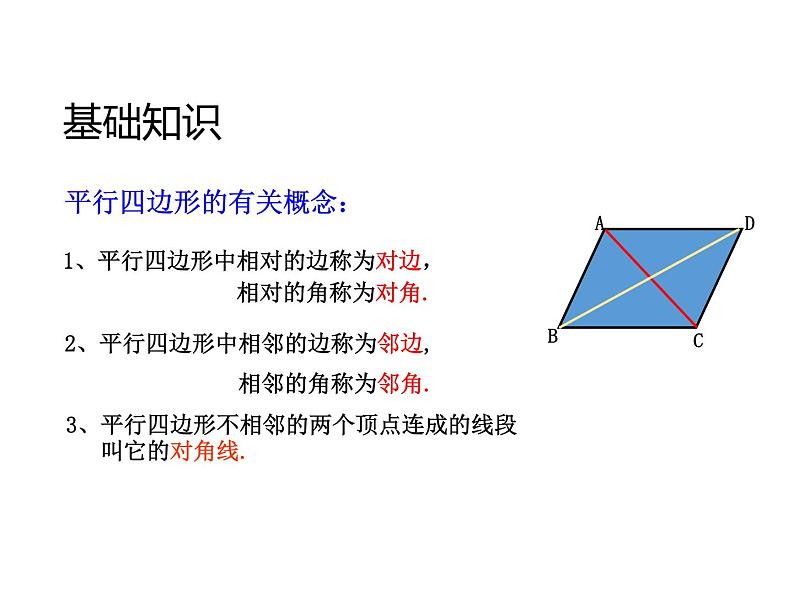
1、平行四边形中相对的边称为对边, 相对的角称为对角.
2、平行四边形中相邻的边称为邻边, 相邻的角称为邻角.
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段 叫它的对角线.
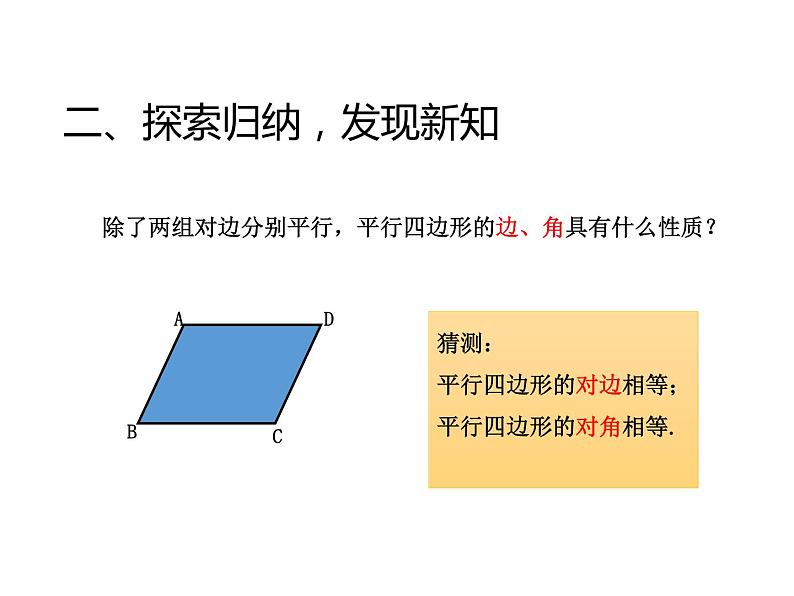
除了两组对边分别平行,平行四边形的边、角具有什么性质?
二、探索归纳,发现新知
猜测:平行四边形的对边相等;平行四边形的对角相等.
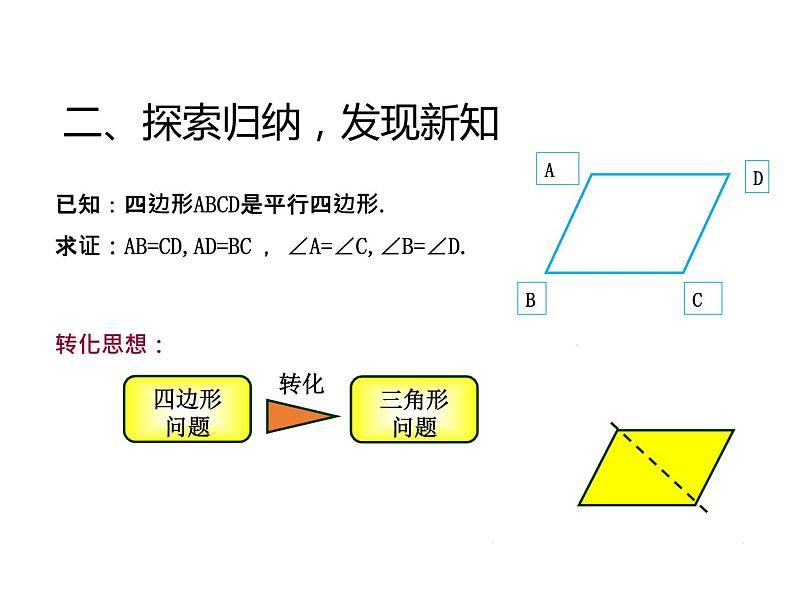
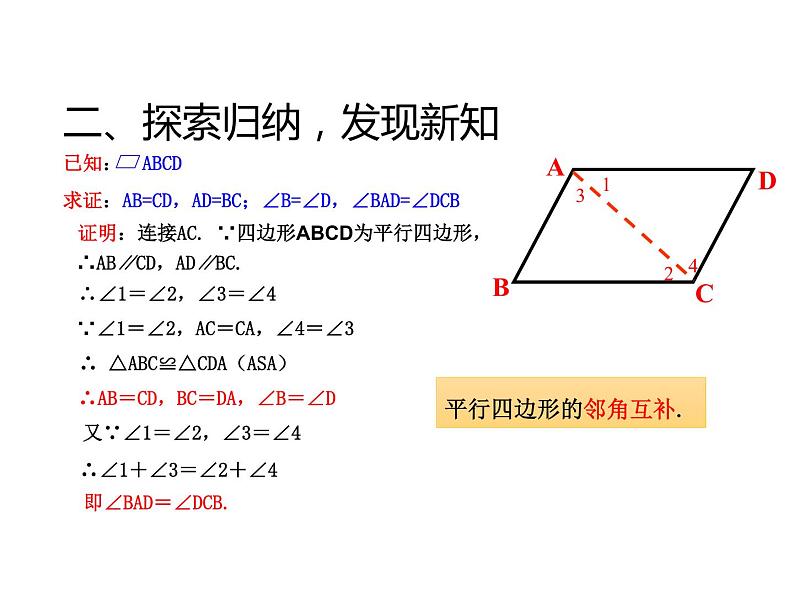
已知:四边形ABCD是平行四边形.求证:AB=CD,AD=BC ,∠A=∠C,∠B=∠D.
即∠BAD=∠DCB.
证明:连接AC. ∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC.
∴∠1=∠2,∠3=∠4
∵∠1=∠2,AC=CA,∠4=∠3
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠3=∠2+∠4
平行四边形的邻角互补.
平行四边形的两组对边分别平行且相等.
∵ 四边形ABCD是平行四边形
∴ AB∥CD,AD∥BC. (平行四边形的对边平行) AB=CD, AD=BC. (平行四边形的对边相等)
∠A=∠C, ∠B=∠D (平行四边形的对角相等)
平行四边形的两组对角分别相等.
三、灵活应用,能力提升
例1 如图,在□ ABCD中,DE⊥AB,BF⊥CD,垂足分别为E、F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∠AED=∠CFB=90°,
∴△ADE≌△CBF.
证明: ∵四边形ABCD是平行四边形,∴ ∠A= ∠C,AD=CB.又∠AED= ∠CFB=90°,∴ △ADE≌△CBF(AAS),∴AE=CF.
思考 在上述证明中还能得出什么结论?
若m // n,作 AB // CD // EF,分别交 m于A、C、E,交 n于B、D、F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.
两条平行线间的距离相等.
若m // n,AB、CD、EF垂直于 n,交n于B、D、F,交 m于A、C、E.
同前面易得AB=CD=EF
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
四、课堂小结,凝练归纳
平行四边形的对边平行且相等.
平行四边形的对角相等.
定义:有两组对边分别平行的四边形是平行四边形.
五、课后练习,拓展提升
1.在□ ABCD中,∠A=50°,则∠C=_____°,∠D=_____.° 2.如果□ ABCD中,∠B+∠D=240°,则∠B= _____°,∠A= _____°. 3.如果□ ABCD的周长为28cm,且AD=4cm,那么BC=____cm,AB=_____cm,CD=_____cm.
人教版八年级下册18.1.1 平行四边形的性质试讲课课件ppt: 这是一份人教版八年级下册18.1.1 平行四边形的性质试讲课课件ppt,共26页。PPT课件主要包含了边特殊,角特殊,全等三角形,平行四边形,学习目标,知识要点1,平行四边形的定义,知识要点2,归纳小结,对边平行且相等等内容,欢迎下载使用。
人教版八年级下册18.1.1 平行四边形的性质精品ppt课件: 这是一份人教版八年级下册18.1.1 平行四边形的性质精品ppt课件,文件包含1811平行四边形的性质第1课时pptx、RJ中学数学八年级下第十八章1811平行四边形的性质第1课时教学详案docx等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
2021学年18.1.1 平行四边形的性质多媒体教学ppt课件: 这是一份2021学年18.1.1 平行四边形的性质多媒体教学ppt课件,文件包含1811平行四边形的性质课件pptx、1811平行四边形的性质教案doc、1811平行四边形的性质练习doc、1811平行四边形的性质学案doc等4份课件配套教学资源,其中PPT共44页, 欢迎下载使用。













