初中数学人教版八年级下册18.2 特殊的平行四边形综合与测试精品课时训练

这是一份初中数学人教版八年级下册18.2 特殊的平行四边形综合与测试精品课时训练，共14页。

一．选择题（共12小题）


1．菱形具有而平行四边形不具有的性质是（ ）


A．对角线互相垂直B．两组对角分别相等


C．对角线互相平分D．两组对边分别平行


2．下列叙述，错误的是（ ）


A．对角线互相垂直且相等的平行四边形是正方形


B．对角线互相垂直平分的四边形是菱形


C．对角线互相平分的四边形是平行四边形


D．对角线相等的四边形是矩形


3．如图，点A、B在直线l1上，点C、D在直线l2上，l1∥l2，CA⊥l1，BD⊥l2，AC＝3cm，则BD等于（ ）cm．





A．1B．2C．3D．4


4．菱形的两条对角线的分别为60cm和80cm，那么边长是（ ）


A．60cmB．50cmC．40cmD．80cm


5．四边形ABCD的对角线AC、BD互相平分，要使它成为矩形，需要添加的条件是（ ）


A．AB＝CDB．AC＝BDC．AB＝BCD．AC⊥BD


6．如图，已知△ABC中，AD是BC边上的中线，则下列结论不一定正确的是（ ）





A．B．BD＝CDC．D．


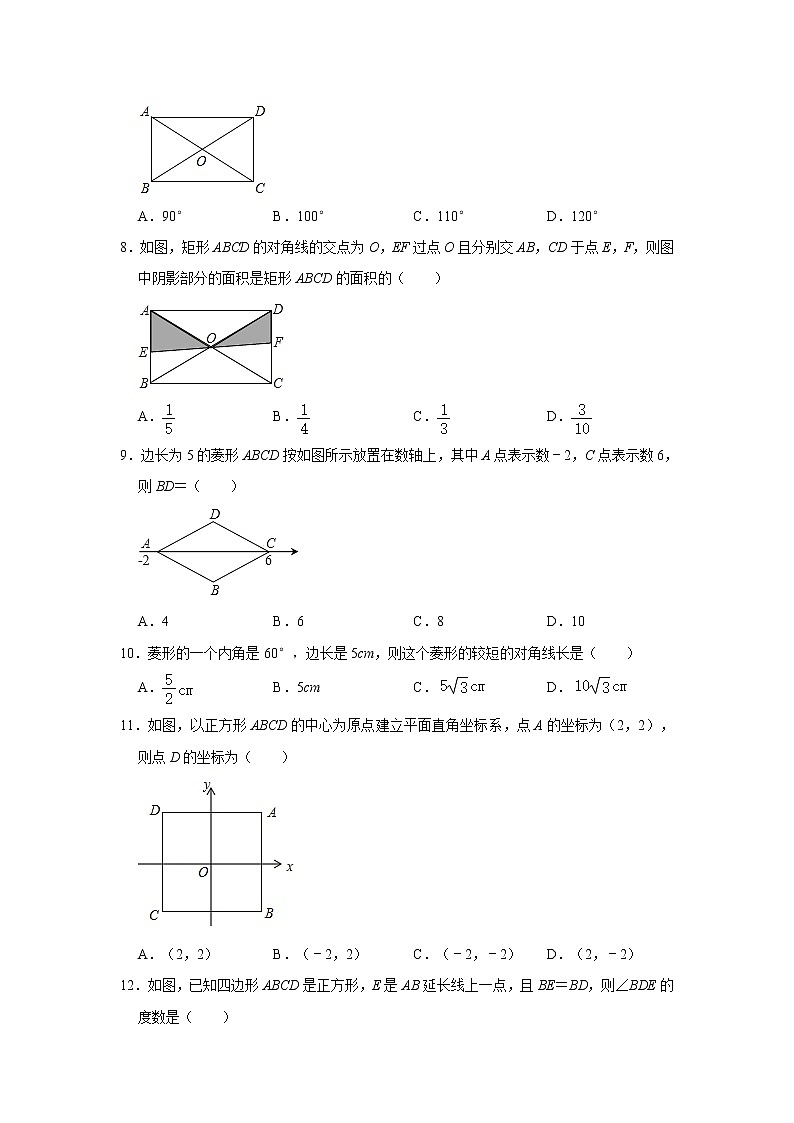
7．如图，在矩形ABCD中，AC与BD交于点O，若AB＝3，AC＝6，则∠AOD等于（ ）





A．90°B．100°C．110°D．120°


8．如图，矩形ABCD的对角线的交点为O，EF过点O且分别交AB，CD于点E，F，则图中阴影部分的面积是矩形ABCD的面积的（ ）





A．B．C．D．


9．边长为5的菱形ABCD按如图所示放置在数轴上，其中A点表示数﹣2，C点表示数6，则BD＝（ ）





A．4B．6C．8D．10


10．菱形的一个内角是60°，边长是5cm，则这个菱形的较短的对角线长是（ ）


A．B．5cmC．D．


11．如图，以正方形ABCD的中心为原点建立平面直角坐标系，点A的坐标为（2，2），则点D的坐标为（ ）





A．（2，2）B．（﹣2，2）C．（﹣2，﹣2）D．（2，﹣2）


12．如图，已知四边形ABCD是正方形，E是AB延长线上一点，且BE＝BD，则∠BDE的度数是（ ）





A．22.5°B．30°C．45°D．67.5°


二．填空题（共8小题）


13．直角三角形斜边上的中线为6，则这它的斜边是 ．


14．平行四边形ABCD对角线互相垂直，若添加一个适当的条件使四边形为正方形．则添加条件可以是 （只需添加一个）．


15．如图，在矩形ABCD中，AC，BD交于点O，M、N分别为BC、OC的中点．若BD＝8，则MN的长为 ．





16．如图，已知菱形ABCD的对角线AC、BD交于点O，OC＝2cm，∠ABO＝30°，则菱形 ABCD的面积是 ．





17．如图，在菱形ABCD中，∠BAD＝45°，DE是AB边上的高，BE＝2，则AB的长是 ．





18．如图，四边形ABCD是正方形，若对角线BD＝4，则BC＝ ．





19．在菱形ABCD中，周长为16，∠ABC＝30°，则其面积为 ．


20．如图，矩形ABCD中，直线MN垂直平分AC，与CD，AB分别交于点M，N．若DM＝2，CM＝3，则矩形的对角线AC的长为 ．





三．解答题（共6小题）


21．如图，已知点C为线段AB上一点，四边形ACMF、BCNE是两个正方形．求证：AN＝BM．





22．如图，在矩形ABCD中，F是CD的中点，连接AF交BC延长线于点E．求证：BC＝EC．





23．矩形ABCD中，AE平分∠BAD交BC于点E，CF平分∠BCD交AD于点F，求证：AE∥CF．





24．如图，四边形ABCD是矩形，E是BD上的一点，∠BAE＝∠BCE，∠AEB＝∠CEB，求证：四边形ABCD是正方形．





25．如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．


（1）求证：四边形AODE是矩形；


（2）若△ABC是边长为2的正三角形，求四边形AODE的面积．





26．如图，在矩形ABCD中，BD的垂直平分线交AD于E，交BC于F，连接BE、DF．


（1）判断四边形BEDF的形状，并说明理由；


（2）若AB＝8，AD＝16，求BE的长．



































参考答案


一．选择题（共12小题）


1．【解答】解：A、正确．对角线互相垂直是菱形具有而平行四边形不具有的性质；


B、错误．两组对角分别相等，是菱形和平行四边形都具有的性质；


C、错误．对角线互相平分，是菱形和平行四边形都具有的性质；


D、错误．两组对边分别平行，是菱形和平行四边形都具有的性质；


故选：A．


2．【解答】解：


A、根据对角线互相垂直的平行四边形可判定为菱形，再有对角线且相等可判定为正方形，故此选项正确，不符合题意；


B、根据菱形的判定方法可得对角线互相垂直平分的四边形是菱形正确，故此选项正确，不符合题意；


C、对角线互相平分的四边形是平行四边形是判断平行四边形的重要方法之一，故此选项正确，不符合题意；


D、根据矩形的判定方法：对角线互相平分且相等的四边形是矩形，因此只有对角线相等的四边形不能判定是矩形，故此选项错误，符合题意；


故选：D．


3．【解答】解：如图，CA⊥l1，BD⊥l2，


∴AC∥BD．


又∵l1∥l2，


∴四边形ABDC是矩形．


∴BD＝AC．


又∵AC＝3cm，


∴BD＝3cm．


故选：C．





4．【解答】解：∵菱形的两条对角线长分别为60cm和80cm，


∴该菱形的边长为，


故选：B．


5．【解答】解：需要添加的条件是AC＝BD；理由如下：


∵四边形ABCD的对角线AC、BD互相平分，


∴四边形ABCD是平行四边形，


∵AC＝BD，


∴四边形ABCD是矩形（对角线相等的平行四边形是矩形）；


故选：B．


6．【解答】解：如图，在△ABC中，AD是BC边上的中线，则BD＝CD＝BC，故选项A、B、D不符合题意．


若∠BAC＝90°时，AD＝BC才成立，否则不成立．故选项C符合题意．


故选：C．





7．【解答】解：∵在矩形ABCD中，AC与BD交于点O，AC＝6，


∴OA＝OB＝AC＝3，


∵AB＝3，


∴OA＝OB＝AB，


∴△OAB是等边三角形，


∴∠AOB＝60°，


∴∠AOD＝180°﹣∠AOB＝120°．


故选：D．


8．【解答】解：∵矩形ABCD的边AB∥CD，


∴∠ABO＝∠CDO，


在矩形ABCD中，OB＝OD，


在△BOE和△DOF中，


，


∴△BOE≌△DOF（ASA），


∴S△BOE＝S△DOF，


∴阴影部分的面积＝S△AOB＝S矩形ABCD．


故选：B．


9．【解答】解：∵A点表示数﹣2，C点表示数6，


∴AC＝8，


∵AD＝5，


∴BD＝2＝6，


故选：B．


10．【解答】解：因为菱形的四边相等，当一个内角是60°，则较短对角线与两边组成等边三角形．


所以这个菱形的较短的对角线长是5cm．


故选：B．


11．【解答】解：如图所示：∵以正方形ABCD的中心O为原点建立坐标系，点A的坐标为（2，2），


∴点B、C、D的坐标分别为：（2，﹣2），（﹣2，﹣2），（﹣2，2）．


故选：B．


12．【解答】解：∵BE＝DB，


∴∠BDE＝∠E，


∵∠DBA＝∠BDE+∠BED＝45°


∴∠BDE＝×45°＝22.5°．


故选：A．





二．填空题（共8小题）


13．【解答】解：∵Rt△ABC斜边上的中线为6，


∴这个三角形斜边长为12．


故答案为：12．


14．【解答】解：∵平行四边形ABCD对角线互相垂直，


∴四边形ABCD是菱形，


当对角线AC＝BD或∠BAD＝90°时，


平行四边形ABCD是矩形，


∴四边形ABCD是正方形；


故答案为：对角线相等或∠BAD＝90°，


15．【解答】解：如图，∵四边形ABCD是矩形，AC，BD交于点O，BD＝8


∴BD＝2BO，即2BO＝8．


∴BO＝4．


又∵M、N分别为BC、OC的中点，


∴MN是△CBO的中位线，


∴MN＝BO＝2．


故答案是：2．





16．【解答】解：∵四边形ABCD是菱形，


∴∠ABO＝∠CBO＝30°，∠BOC＝90°，


∵OC＝2cm，


∴OB＝2cm，


∴＝cm2．


∴菱形ABCD的面积为2cm2．


故答案为：8cm2．


17．【解答】解，设AB＝x，


∵四边形ABCD是菱形，


∴AD＝AB＝x，


∵DE是AB边上的高，


∴∠AED＝90°，


∵∠BAD＝45°，


∴∠BAD＝∠ADE＝45°，


∴AE＝ED＝x﹣2，


由勾股定理得：AD＝AE2+DE2，


∴x2＝（x﹣2）2+（x﹣2）2，


解得：x1＝4+2，x2＝4﹣2，


∵BE＝2，


∴AB＞2，


∴AB＝x＝4+2，


故答案为：4+2．


18．【解答】解：∵四边形ABCD是正方形，


∴CD＝BC，∠C＝90°，


∴△BCD是等腰直角三角形，


∴BD＝BC＝4，


∴BC＝2，


故答案为：2．


19．【解答】解：如图，过点A作AE⊥BC于点E，





∵菱形ABCD的周长为16，


∴AB＝BC＝4，


∵∠ABC＝30°，AE⊥BC，


∴AE＝AB＝2，


∴菱形ABCD的面积＝BC×AE＝8，


故答案为：8．


20．【解答】解：如图，连接AM．


∵直线MN垂直平分AC，


∴MA＝MC＝3，


∵四边形ABCD是矩形，


∴∠D＝90°，


∵DM＝2，MA＝3，


∴AD2＝AM2﹣DM2＝32﹣22＝5，


∴AC＝＝＝；


故答案为：．





三．解答题（共6小题）


21．【解答】证明：∵四边形ACMF和四边形CBEN都是正方形，


∴AC＝CM，NC＝BC，∠ACN＝∠BCM＝90°，


∴△ACN≌△MCB（SAS），


∴AN＝BM．


22．【解答】证明：∵四边形ABCD是矩形，


∴AD∥BE，AD＝BC，


∴∠ADF＝∠ECF，∠DAF＝∠CEF，


∵F是CD的中点，


∴DF＝CF，


∴在△ADF和△ECF中，





∴△ADF≌△ECF（AAS）．


∴AD＝EC，而AD＝BC


∴BC＝EC．


23．【解答】证明：∵四边形ABCD是矩形，


∴AD∥BC，∠BAD＝∠BCD＝90°，


∴∠AEB＝∠DAE，


∵AE平分∠BAD，CF平分∠BCD，


∴∠DAE＝∠BAD＝45°，∠BCF＝∠BCD＝45°，


∴∠AEB＝∠DAE＝∠BCF，


∴AE∥CF．


24．【解答】法一：


证明：连结AC交BD于O点，如图，


在△AEO与△CEO中，


，


∴△AEO≌△CEO（AAS），


∴AE＝CE，


∴△AEC为等腰三角形，


∵四边形ABCD是矩形，


∴OA＝OC，


∴OE⊥AC，


即AC⊥BD，


∴AC和BD互相垂直平分，


∴四边形ABCD为菱形，


而∠ABC＝90°，


∴四边形ABCD是正方形．


法二：


在△ABE和△CBE中


，


∴△ABE≌△CBE（AAS），


∴BA＝BC，


∵四边形ABCD是矩形，


∴四边形ABCD是正方形．





25．【解答】（1）证明：∵DE∥AC，AE∥BD，


∴四边形AODE是平行四边形，


∵四边形ABCD是菱形，


∴AC⊥BD，


∴∠AOD＝90°，


∴四边形AODE是矩形；


（2）解：∵△ABC是边长为2的正三角形，


∴AB＝AC＝2，


∠ABC＝60°，


∵四边形ABCD为菱形，


∴AO＝AC＝1，OD＝OB，


∵∠AOB＝90°，


∴OB＝＝＝，


∴OD＝OB＝，


∵四边形AODE是矩形，


∴四边形AODE的面积＝×1＝．


26．【解答】解：（1）四边形BEDF是菱形；理由如下：


∵EF是BD的垂直平分线，


∴BE＝DE，BF＝DF，


∴∠EBD＝∠EDB，


∵四边形ABCD是矩形，


∴AD∥BC，


∴∠DBF＝∠EDB，


∴∠EBD＝∠DBF，


∵BD⊥EF，


∴BE＝BF，


∴BE＝DE＝DF＝BF，


∴四边形BEDF是菱形；


（2）∵四边形ABCD是矩形，


∴∠A＝90°，


由（1）知：BE＝DE


设BE＝DE＝x，则AE＝AD﹣x＝16﹣x，


在Rt△ABE中，AB2+AE2＝BE2，


即82+（16﹣x）2＝x2，


解得：x＝10，


∴BE的长为10．