人教版七年级下册第六章 实数综合与测试一等奖复习课件ppt

这是一份人教版七年级下册第六章 实数综合与测试一等奖复习课件ppt，共26页。PPT课件主要包含了有关概念，一平方根与立方根，做一做，判断题，不要搞错了，117和，下列说法正确的是，实数的性质，掌握规律等内容，欢迎下载使用。

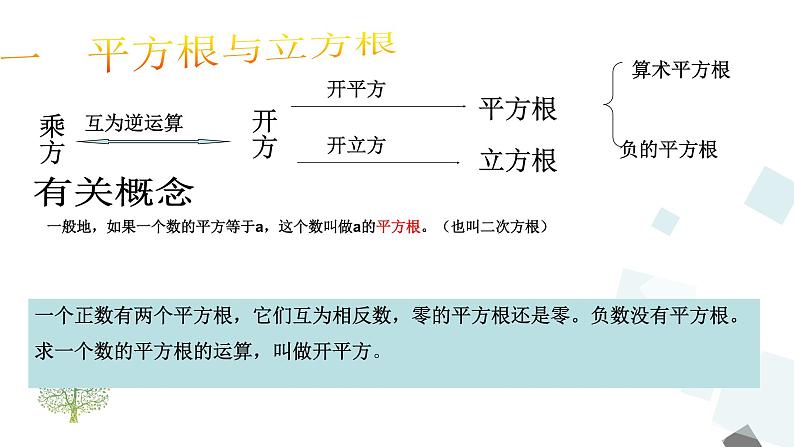
一个正数有两个平方根，它们互为相反数，零的平方根还是零。负数没有平方根。求一个数的平方根的运算，叫做开平方。
正数a的正的平方根和零的平方根,统称算术平方根 。非负数a的算术平方根是非负数， 。
求一个数的立方根（三次方根）的运算，叫做开立方，开立方与立方互为逆运算。
1、平方根的定义：若X2=a，则X就叫做a的__________。a的平方根用________表示
2、平方根的性质 （1）一个正数有 平方根，它们互为________（2）0的平方根还是____ （3）负数_______平方根
3、平方根的求法： 如求4的平方根： ∵ (±2)2 = 4　　　 ∴4的平方根是±2　
1、立方根的定义：若X3=a，则X就叫做a的________。a的立方根用 表示
2、立方根的性质 （1）一个正数的立方根___________ （2）0的立方根还是_____ （3）负数的立方根________
3、立方根的求法： 如求8的立方根： ∵ 23 = 8　　　 ∴8的立方根是2　
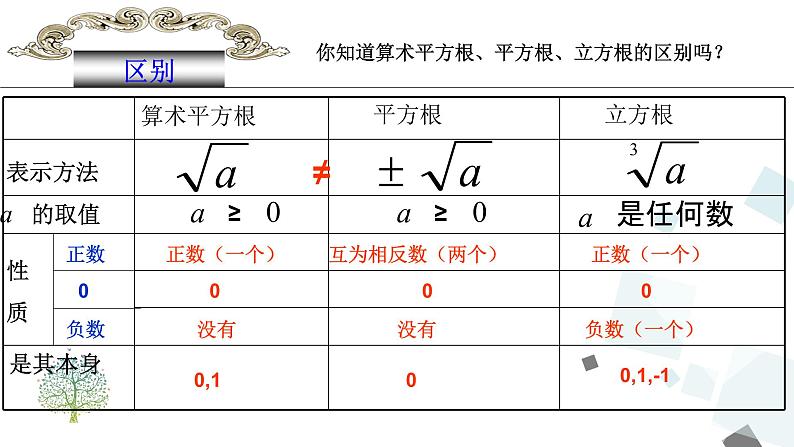
你知道算术平方根、平方根、立方根的区别吗？
对于 的值得讨论
（1） （2） －27（3） 0
求下列各数的算术平方根：
（1） 16 （2）5
算术平方根是它本身的数有______________。
平方根 ，立方根呢？
5、若某数的一个立方根是4，则这个数的平方根是 ；
6、(-4)2的算术平方是 ；
9、-64的立方根是 ；
比较下列各组里两个数的大小.
1.无理数有几个？ 2.无理数都是用根号表示的数吗？3.无理数都是开方开不尽的数吗？4.用根号表示的数都是无理数吗？
有理数和无理数统称实数.
（1）无限小数是无理数
（2）有理数都是有限小数
（3）一个数的立方根不一定是无理数
（4）任何实数都有唯一的立方根
（5）只有正实数才有算术平方根
（6）任何数的平方根有两个，它们互为相反数
数a的相反数是-a.
一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数； 0的绝对值是0.
1、求下列各数的相反数、倒数和绝对值：
如果把所有的有理数都标到数轴上，那么数轴将被填满了．（ ）
4.判断对错,并说明理由．
每一个实数都可用数轴上的一个点来表示．
数轴上的每一个点都表示一个实数．
大家都知道 是无理数，而无理数是无限不循环小数，因此， 的小数部分我们不可能全部写出来，于是小明用 来表示 的小数部分，你同意小明的方法吗？事实上，小明的表示方法是有道理的，因为 的整数部分是1，将这个数减去其整数部分，差就是小数部分。
的整数部分是___,小数部分是______.
当方程中出现平方时，若有解，一般都有两个解
当方程中出现立方时，一般都有一个解
注意平方根和立方根的移位法则
里面的数的符号化简绝对值要看它
一个正数的平方根是2a-3与5-a,你能求出a吗？
解:（2a-3）+（5-a）=0
解得 a=-2
∴2a-3=-7, 5-a=7
你知道这个正数是多少吗？
跟踪练习 已知5x+19的立方根是4，求2x+7的平方根