人教版八年级下册18.1.2 平行四边形的判定复习课件ppt

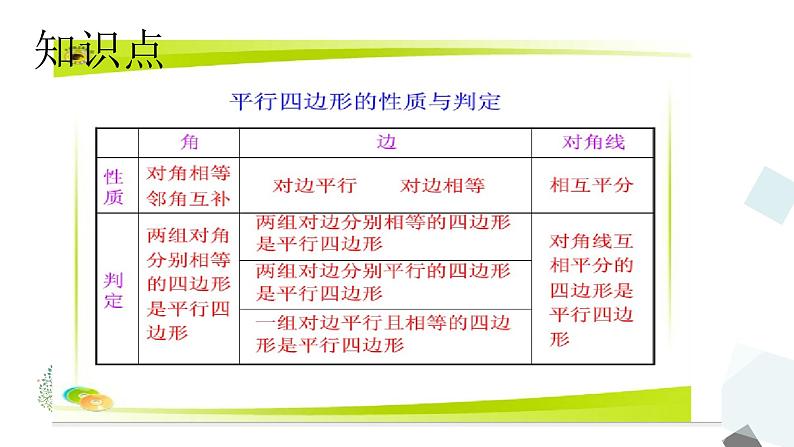
这是一份人教版八年级下册18.1.2 平行四边形的判定复习课件ppt，共10页。PPT课件主要包含了学习目标，知识点，练一练等内容，欢迎下载使用。
1、理解平行四边形的定义，掌握平行四边形的性质和判定2、熟练运用平行四边形的性质和判定进行相关计算和证明。重点：熟练运用平行四边形的性质和判定进行相关计算和证明。难点：选择恰当的方法解决有关平行四边形的问题。
1、（1）在 ABCD中，已知AB=8，AO=3，∠B=50° 则CD=________，AC=________∠A=________，∠D=___________
（2）在 ABCD中， ∠A+ ∠C= 150°那么∠A=__________，∠D=_________
（3）在 ABCD中， ∠A:∠B= 4:5，那么∠B=__________，∠C=_________
3、（呼和浩特）如上右图所示，已知E，F，G，H是四边形ABCD各边的中点，则S四边形EFGH：S四边形ABCD的值是_________．
2、如下左图所示，在四边形ABCD中，AB∥CD，要使四边形ABCD为平行四边形，则应添加的条件是________．（添加一个即可）
4．能够判定四边形ABCD是平行四边形的题设是（ ）． A．AB∥CD，AD=BC B．∠A=∠B，∠C=∠D C．AB=CD，AD=BC D．AB=AD，CB=CD5．具备下列条件的四边形中，不能确定是平行四边形的为（ ）． A．相邻的角互补 B．两组对角分别相等 C．一组对边平行，另一组对边相等 D．对角线交点是两对角线中点6．如下图所示，四边形ABCD的对角线AC和BD相交于点O，下列判断正确的是（ ）． A．若AO=OC，则ABCD是平行四边形; B．若AC=BD，则ABCD是平行四边形; C．若AO=BO，CO=DO，则ABCD是平行四边形; D．若AO=OC，BO=OD，则ABCD是平行四边形
7．如图所示，在四边形ABCD中AB=CD，BC=AD，E，F为对角线AC上的点，且AE=CF，求证：BE=DF．
证明：∵AB=CD，BC=AD， ∴四边形ABCD是平行四边形． ∴AB∥CD， ∴∠BAE=∠DCF． 又∵AE=CE， ∴△ABE≌△CDF（SAS）， ∴BE=EF．
8．如图所示，D为△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．求证：CD=AF．
证明：∵FC∥AB， ∴∠DAC=∠ACF，∠ADF=∠DFC． 又∵AE=CE， ∴△ADE≌△CFE（AAS）， ∴DE=EF． ∵AE=CE， ∴四边形ADCF为平行四边形． ∴CD=AF．
9．如图所示，在ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE，BF交于点M，连接CF，DE交于点N，求证：MN∥AD且MN=
10、如图所示，在△ABC中，E为AB的中点，CD平分∠ACB，AD⊥CD于点D．试说明：（1）DE∥BC．（2）DE=
解：延长AD交BC于F． （1）∵AD⊥CD， ∴∠ADC=∠FDC=90°． ∵CD平分∠ACB，∴∠ACD=∠FCD． 在△ACD与△FCD中， ∠ADC=∠FDC，DC=DC，∠ACD=∠FCD． ∴△ACD≌△FCD，∴AC=FC，AD=DF．又∵E为AB的中点，∴DE∥BF，即DE∥BC．