初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教课内容课件ppt

这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教课内容课件ppt，共19页。PPT课件主要包含了学习目标，平行四边形的性质，平行四边形的对边平行，平行四边形的对边相等，平行四边形的对角相等，平行四边形的邻角互补，温故知新，证一证，大显身手，看谁最快等内容，欢迎下载使用。

1、经历并了解平行四边形的判别方法探索过程，我们可以逐步掌握说理的基本方法。2、探索并了解平行四边形的判别方法：两条对角线互相平分的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形。3、能根据判别方法进行有关的应用。重点：平行四边形的判定方法及应用难点：平行四边形的判定定理的灵活应用
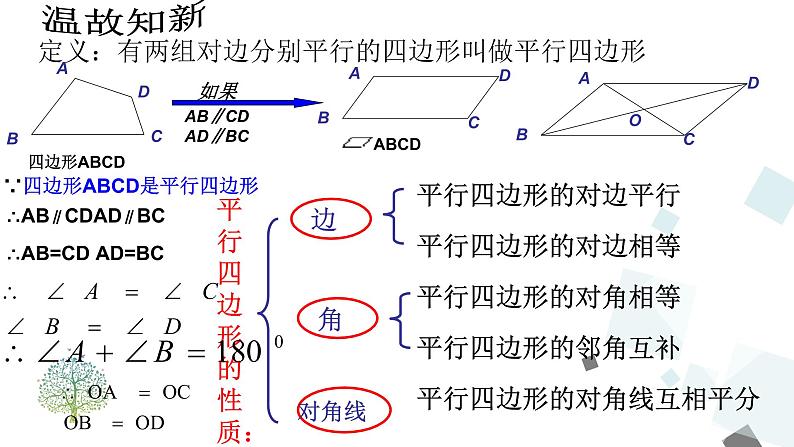
定义：有两组对边分别平行的四边形叫做平行四边形
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD AD=BC
∴AB∥CDAD∥BC
我们知道了平行四边形的性质，那么，有哪些方法可以判断一个四边形是平行四边形呢？（1）根据定义：两组对边分别平行的四边形叫做平行四边形 因为AB//CD,AD//BC; 所以四边形ABCD是平行四边形。
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
思考 我们得到的这些逆命题是否都成立？这节课我们一起探讨一下吧.
平行四边形上面的三条性质的逆命题各是什么？
两组对角分别相等的四边形是平行四边形；
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形；
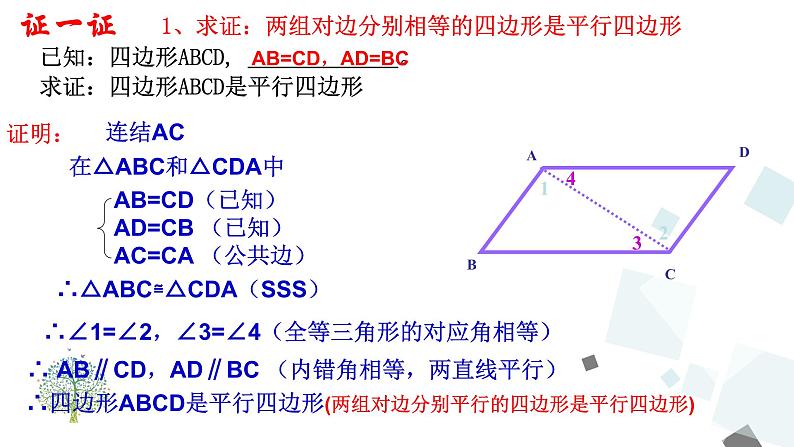
已知：四边形ABCD, 。求证：四边形ABCD是平行四边形
在△ABC和△CDA中
∴△ABC≌△CDA（SSS）
∴∠1=∠2，∠3=∠4（全等三角形的对应角相等）
∴ AB∥CD，AD∥BC （内错角相等，两直线平行）
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
1、求证：两组对边分别相等的四边形是平行四边形
AB=CD，AD=BC
两组对边分别相等的四边形是平行四边形
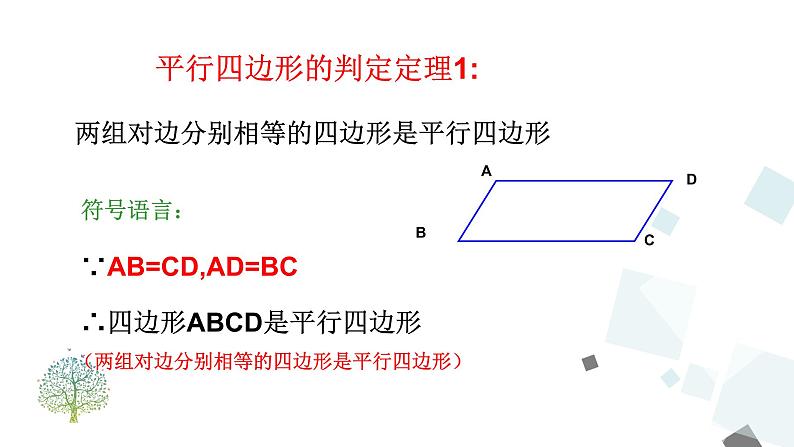
平行四边形的判定定理1:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
（两组对边分别相等的四边形是平行四边形）
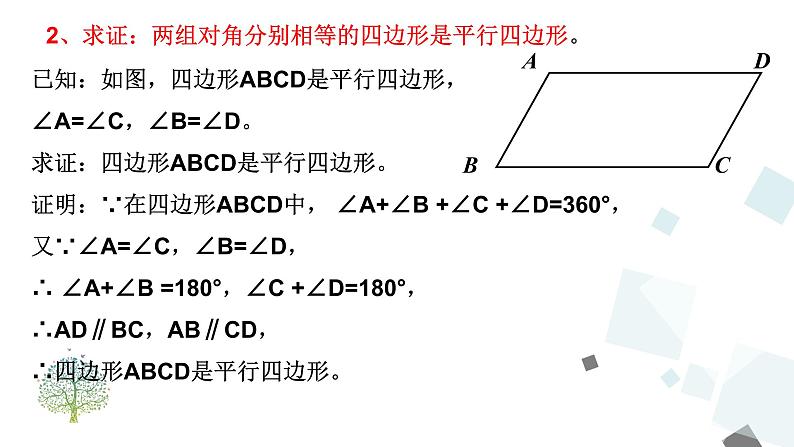
2、求证：两组对角分别相等的四边形是平行四边形。
已知：如图，四边形ABCD是平行四边形，∠A=∠C，∠B=∠D。求证：四边形ABCD是平行四边形。证明：∵在四边形ABCD中， ∠A+∠B +∠C +∠D=360°，又∵∠A=∠C，∠B=∠D，∴ ∠A+∠B =180°，∠C +∠D=180°，∴AD∥BC，AB∥CD，∴四边形ABCD是平行四边形。
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理2:
∵∠A=∠C，∠B=∠D
（两组对角分别相等的四边形是平行四边形）
已知：四边形ABCD中，OA=OC，OB=OD.求证：四边 形ABCD是平行四边形.
在△AOB和△COD中,
OA=OC (已知)，
OB=OD (已知)，
∠AOB=∠COD (对顶角相等)，
∴△AOB≌△COD(SAS)，
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO,
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形.
3、求证：对角线互相平分的四边形是平行四边形。
对角线互相平分的四边形是平行四边形
平行四边形的判定定理3:
∵ OA=OC，OB=OD
(对角线互相平分的四边形是平行四边形)
我们知道两组对边分别平行或相等的四边形是平行四边形。如果只考虑四边形的一组对边，他们满足什么条件时这个四边形能成为平行四边形呢？
如果一个四边形是平行四边形，那么它的任意一组对边平行且相等，反过来一组对边平行且相等的四边形是平行四边形吗？
求证：四边形ABCD是平行四边形。
又∵AD=BC，AC=AC，
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
4、求证：一组对边平行且相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理4:
∵AB CD
（一组对边平行且相等的四边形是平行四边形）
例1：已知：如图：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF.
证明：作对角线BD，交AC于点O. ∵四边形ABCD是平行四边形 ∴ AO=CO，BO=DO ∵AE=CF ∴AO-AE=CO-CF 即EO=FO 又 BO=DO ∴ 四边形BFDE是平行四边形
求证：四边形BFDE是平行四边形
∵四边形ABCD是平行四边形，
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等)，
∵E,F分别是AD,BC的中点，
∴四边形EBFD是平行四边形（一组对边平行并且相等的四边形是平行四边形）。
∴BE=DF(平行四边形的对边分别相等)。
2.如图，AB =DC=EF, AD=BC，DE=CF,则图中有哪些互相平行的线段？
AB ∥ DC∥ EF
说出你这节课的收获和体验让大家与你分享吗？