人教版第十七章 勾股定理综合与测试复习ppt课件

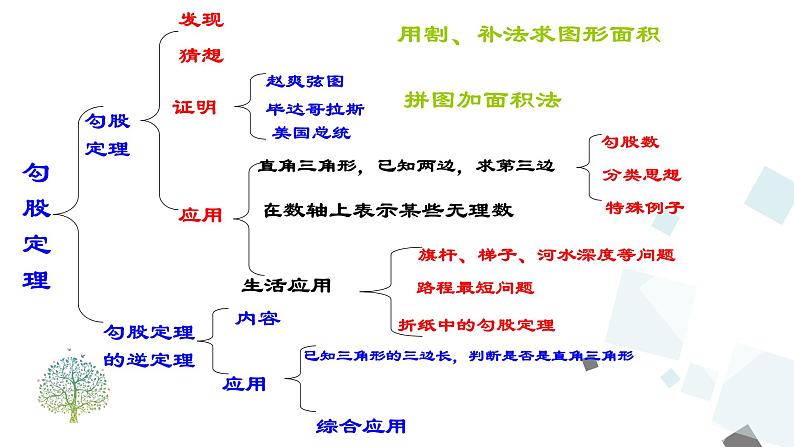
这是一份人教版第十七章 勾股定理综合与测试复习ppt课件，共19页。PPT课件主要包含了勾股定理，拼图加面积法，补法求图形面积，要树立方程思想，综合运用解决问题，整体思想，割补图形，转化思想等内容，欢迎下载使用。
学习目标：　1．回顾本章知识，在回顾过程中主动构建起本章知识结构；　2．思考勾股定理及其逆定理的发现证明和应用过程，体会方程思想、分类讨论思想、数形结合思想、转化思想在解决数学问题中的作用.学习重点、难点： 勾股定理及其逆定理的综合应用．
在数轴上表示某些无理数
旗杆、梯子、河水深度等问题
已知三角形的三边长，判断是否是直角三角形
1.在Rt△ABC中，∠C=90°.（1）如果a=3，b=4， 则c=　　　　 ；（2）如果a=12，c=20， 则b=　　　　；（3）如果c=13，b=12，则a=　　　　 ； （4）已知b=3，∠A=30°，求a，c.
答案:（4）a= ，c= .
2、在Rt△ABC中，已知a=1，b=3，∠B=90°，则第三边c的长为　　　　．
4、分别以下列四组数为一个三角形的边长：①3，4，5；②5，12，13；③8，15，17；④4，5，6．其中能构成直角三角形的有 　　　 ．
3、在Rt△ABC中，已知a=1，b=3，则第三边c的长为 ．
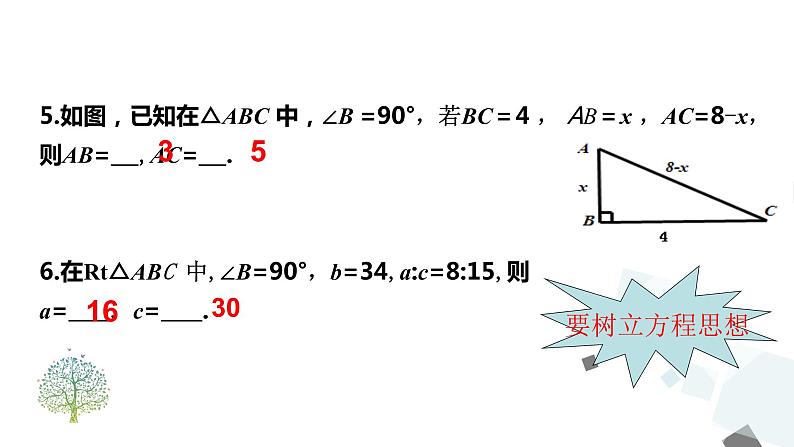
5.如图，已知在△ABC 中，∠B =90°，若BC＝4 ， AB＝x ，AC=8-x，则AB= ,AC= .6.在Rt△ABC 中,∠B=90°，b=34,a:c=8:15,则a= , c= .
1．证明线段相等.已知：如图，AD是△ABC的高，AB=10，AD=8，BC=12 .求证： △ABC是等腰三角形.
证明：∵AD是△ABC的高，∴∠ADB=∠ADC=90°.∵在Rt△ADB中，AB=10，AD=8，∴BD=6 .∵BC=12, ∴DC=6.∵在Rt△ADC中，AD=8，∴AC=10，∴AB=AC.即△ABC是等腰三角形.
 分析：利用勾股定理求出线段BD的长，也能求出线段AC的长，最后得出AB=AC，即可.
2．解决折叠的问题.已知如图，将长方形的一边BC沿CE折叠，使得点B落在AD边的点F处，已知AB=8，BC=10, 求BE的长.
【思考】1、由AB=8，BC=10,你可以知道哪些线段长？2、在Rt△DFC中，你可以求出DF的长吗？3、由DF的长，你还可以求出哪条线段长？4、设BE = x，你可以用含有x的式子表示出哪些线段长？
已知如图，将长方形的一边BC沿CE折叠，使得点B落在AD边的点F处，已知AB=8，BC=10, 求BE的长.
解:设BE=x，折叠，∴△BCE ≌△FCE， ∴BC=FC=10. 令BE=FE=x，长方形ABCD，∴ AB=DC=8 ，AD=BC=10，∠D=90°，∴DF=6, AF=4，∠A=90°, AE=8-x ， ∴ ，解得 x = 5 .∴BE的长为5.
3.做高线，构造直角三角形.已知：如图，在△ABC中，∠B=45°，∠C=60°，AB=2.求（1）BC 的长；（2）S△ABC .
分析：由于本题中的△ABC不是直角三角形，所以添加BC边上的高这条辅助线，就可以求得BC及S△ABC .
解：当高AD在△ABC内部时，如图①.在Rt△ABD中，由勾股定理，得BD2＝AB2－AD2＝202－122＝162，∴BD＝16.在Rt△ACD中，由勾股定理，得CD2＝AC2－AD2＝152－122＝81，∴CD＝9.∴BC＝BD＋CD＝25，∴△ABC的周长为25＋20＋15＝60.
在△ABC中，AB＝20，AC＝15，AD为BC边上的高，且AD＝12，求△ABC的周长．
题中未给出图形，作高构造直角三角形时，易漏掉钝角三角形的情况．如在本例题中，易只考虑高AD在△ABC内的情形，忽视高AD在△ABC外的情形．
当高AD在△ABC外部时，如图②.同理可得 BD＝16，CD＝9.∴BC＝BD－CD＝7，∴△ABC的周长为7＋20＋15＝42.综上所述，△ABC的周长为42或60.
（1）已知Rt△ABC中，∠C=90°，若a+b=14，c=10，则Rt△ABC的面积是_______
解析：（a+b）²=a²+b²+2ab=c²+2ab 所以ab=48
（2）一个直角三角形的周长为24cm，面积为24cm²，则斜边长为_____
如图，一条河同一侧的两村庄A、B，其中A、B到河岸最短距离分别为AC=1km，BD=2km，CD=4km，现欲在河岸上M处建一个水泵站向A、B两村送水，当M在河岸上何处时，到A、B两村铺设水管总长度最短，并求出最短距离。
6、勾股定理与最短距离问题
2、如图，将一根25cm长的细木棍放入长，宽高分别为8cm、6cm、和 cm的长方体无盖盒子中，求细木棍露在外面的最短长度是多少？
1、如图，四边形ABCD中，∠B＝900，AB＝20，BC＝15，CD＝7，AD＝24,求证∠A+ ∠C=1800。
2、如图所示是一块地，已知AD=8米，CD=6米，∠D=900，AB=26米，BC=24米，求这块地的面积
8、 格点三角形 ∠ BCD是直角吗