初中人教版17.2 勾股定理的逆定理课文配套ppt课件

这是一份初中人教版17.2 勾股定理的逆定理课文配套ppt课件，共21页。PPT课件主要包含了巩固新知，勾股定理逆定理的证明，勾股定理性质定理，互逆命题，定理与逆定理，定理应用等内容，欢迎下载使用。
学习目标（1）理解勾股定理的逆定理.（2）了解互逆命题、互逆定理。（3）能证明勾股定理的逆定理，能利用勾股定理的逆定理判 断一个三角形是直角三角形.重点：勾股定理的逆定理证明及简单应用；难点：能利用勾股定理的逆定理判断一个三角形是直角三角形.
　　勾股定理　如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2+b2=c2．
　　题设（条件）：直角三角形的两直角边长为a，b，斜边长为c ．
　　结论：a2+b2=c2．
一、　回忆勾股定理的内容．
反过来，如果一个三角形的三边长a、b、c满足a2+b2=c2 .那么这个三角形的形状怎样？
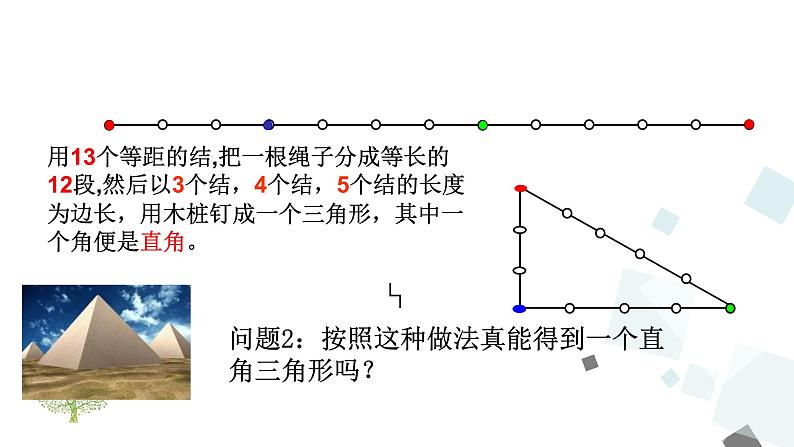
古埃及人曾用下面的方法得到直角
问题2：按照这种做法真能得到一个直角三角形吗？
用13个等距的结,把一根绳子分成等长的12段,然后以3个结，4个结，5个结的长度为边长，用木桩钉成一个三角形，其中一个角便是直角。
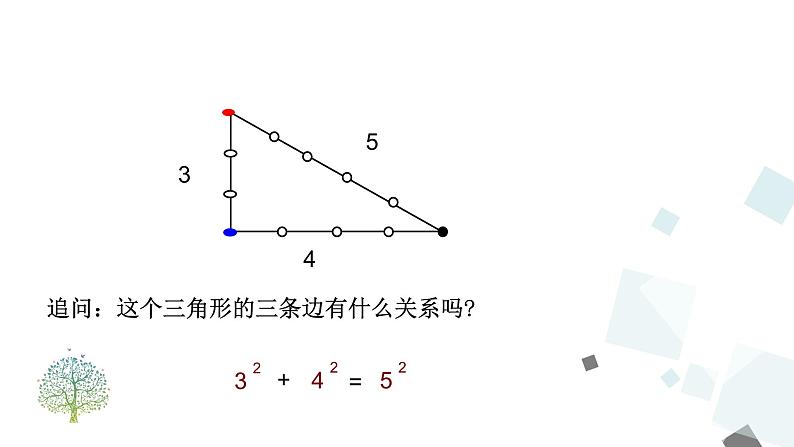
追问：这个三角形的三条边有什么关系吗?
（1）下列各组数中两个数的平方和等于第三个数的平方，分别以这些数为边长（单位：cm）画三角形：
　　①2.5，6，6.5；②4，7.5，8.5.
（2）量一量：用量角器分别测量上述各三角形的最大角的度数.（3）想一想：判断这些三角形的形状，提出猜想.
实验操作 提出猜想
问题2 由上面几个例子你发现了什么吗?请以命题的形式说出你的观点!
思考：上节课的命题1和本节课的命题2的题设、结论分别是什么？
互逆命题的定义：如果两个命题的题设和结论正好相反，那么这样的两个命题叫做互逆命题。　　如果把其中一个叫做原命题，那么另一个叫做它的逆命题。
怎样得到一个命题的逆命题？
把一个命题的题设和结论交换一下，即可得到它的逆命题
(1)两条直线平行，内错角相等．(2)如果两个实数相等，那么它们的平方相等．(3)如果两个实数相等，那么它们的绝对值相等．(4)全等三角形的对应角相等．
说出下列命题的逆命题．并判断这些命题的逆命题成立吗?
逆命题: 内错角相等，两条直线平行. 成立
逆命题:如果两个实数的平方相等，那么这两个实数相等. 不成立
逆命题:如果两个实数的绝对值相等，那么这两个实数相等. 不成立
逆命题:对应角相等的两个三角形是全等三角形. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
一个命题是真命题,它逆命题却不一定是真命题.
已知:在△ABC中，AB=c BC=a CA=b 且a2+b2=c2
求证:△ ABC是直角三角形.
证明:画一个△A’B’C’,使∠ C’=90°,B’C’=a, C’A’=b
∴ A’B’ 2=c2
∴ A’B’2= a2+b2
在△ ABC和△ A’B’C’中
∴ △ ABC ≌△ A’B’C’（SSS）
∴ ∠ C= ∠ C/=90°
则 △ ABC是直角三角形（直角三角形的定义）
勾股定理的逆定理是直角三角形的判定定理，即已知三角形的三边长，且满足两条较小边的平方和等于最长边的平方，即可判断此三角形为直角三角形 ，最长边所对应的角为直角.
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
回想一下：我们学过哪几对互逆定理？
互逆命题与互逆定理有何关系?
互逆定理一定是互逆命题，但是互逆命题不一定是互逆定理。
我们已经学习了一些互逆的定理,如: (1)勾股定理及其逆定理；(2)两直线平行,内错角相等; (3) 内错角相等,两直线平行. (4)角的平分线的性质与判定； (5)线段的垂直平分线的性质与判定.
(1) a＝15 , b ＝8 , c＝17
(2) a＝13 , b ＝14 , c＝15
分析：根据勾股定理的逆定理，一个三角形中两条较小边长的平方和等于最大边长的平方，那么这个三角形是直角三角形
例1 判断由a、b、c组成的三角形是不是直角三角形：
解（1）152＋82＝225＋64＝289 172＝289 ∴ 152＋82＝172 ∴这个三角形是直角三角形 （2）132+142=169+196=365 152=225 因为132+142≠152， 根据勾股定理，这个三角形不是三角形.
勾股数 ：像15、8、17这样 能够成为直角三角形三条边长的三个正整数，称为勾股数
3，4，5；5，12，13；6，8，10；7，24，25；8，15，17；9，40，41；10，24，26等等.
一组勾股数，都扩大相同倍数k(k为正整数)，得到一组新数，这组数同样是勾股数.
1、下列四组数中：①1、 、2；②32，42，52 ；③9，40，41；④3k、4k、5k（k为正整数）.属于勾股数的有____________(填序号).2、直角三角形一条直角边与斜边分别为8cm和10cm.则斜边上的高等于    cm.3、已知两条线段的长为3cm和4cm,当第三条线段的长为     cm时,这三条线段能组成一个直角三角形.
4、判断由线段a、b、c组成的三角形是不是直角三角形：
（1）a=7，b=24，c=25； （2）a= ，b=4，c=5；
解：(1)因为a2+b2=49+576=625， c2=252=625 a2+b2=c2 所以，根据勾股定理的逆定理，a、b、c组成的三角形是直角三角形
(2)因为b2+c2=16+25=41， a2=41 b2+c2=a2 所以，根据勾股定理的逆定理，a、b、c组成的三角形是直角三角形
（3）a= ，b= 1，c= （4）a=40，b=50，c=60.
解：(3)因为c2+b2= ， a2= c2+b2=a2 所以，根据勾股定理的逆定理，a、b、c组成的三角形是直角三角形
(4)因为a2+b2=1600+2500=4100， c2=3600 ， a2+b2≠c2 所以，根据勾股定理的逆定理，a、b、c组成的三角形不是直角三角形