初中数学人教版八年级下册第十八章 平行四边形综合与测试优质课件ppt

这是一份初中数学人教版八年级下册第十八章 平行四边形综合与测试优质课件ppt，共18页。PPT课件主要包含了平行四边形等内容，欢迎下载使用。

【例1】(永州中考)如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.(1)求证：BE＝CD；(2)连接BF，若BF⊥AE，∠BEA＝60°，AB＝4，求▱ABCD的面积．分析：(1)证AB＝BE，AB＝CD，即可得到结论；(2)将▱ABCD的面积转化为△ABE的面积求解即可.
【对应训练】1．在平面直角坐标系中，以O(0，0)，A(1，1)，B(3，0)为顶点，构造平行四边形，下列各点中不能作为平行四边形顶点坐标的是( )A．(－3，1) B．(4，1)C．(－2，1) D．(2，－1)2．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，点D在BC上，以AC为对角线的所有▱ADCE中，DE最小的值是( )A．2 B．3 C．4 D．5
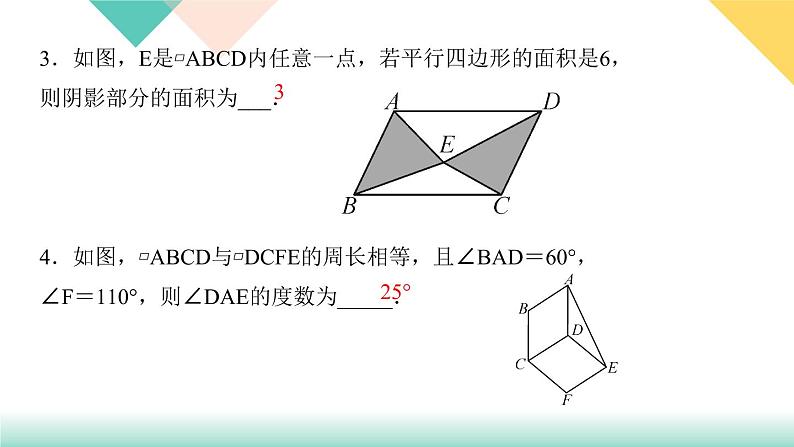
3．如图，E是▱ABCD内任意一点，若平行四边形的面积是6，则阴影部分的面积为___．4．如图，▱ABCD与▱DCFE的周长相等，且∠BAD＝60°，∠F＝110°，则∠DAE的度数为_____．
5．(曲靖中考)如图，在平行四边形ABCD的边AB，CD上截取AF，CE，使得AF＝CE，连接EF，点M，N是线段EF上两点，且EM＝FN，连接AN，CM.(1)求证：△AFN≌△CEM；(2)若∠CMF＝107°，∠CEM＝72°，求∠NAF的度数．(1)证明：∵四边形ABCD是平行四边形，∴CD∥AB，∴∠AFN＝∠CEM，∵FN＝EM，AF＝CE，∴△AFN≌△CEM(SAS)　(2)解：∵△AFN≌△CEM，∴∠NAF＝∠ECM，∵∠CMF＝∠CEM＋∠ECM，∴107°＝72°＋∠ECM，∴∠ECM＝35°，∴∠NAF＝35°
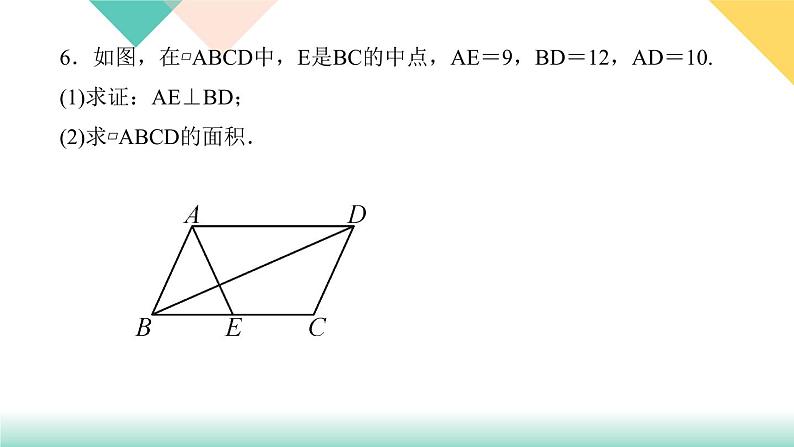
6．如图，在▱ABCD中，E是BC的中点，AE＝9，BD＝12，AD＝10.(1)求证：AE⊥BD；(2)求▱ABCD的面积．
【例2】(2019·郴州)如图，▱ABCD中，点E是边AD的中点，连接CE并延长交BA的延长线于点F，连接AC，DF.求证：四边形ACDF是平行四边形．分析：利用平行四边形的性质，即可判定△FAE≌△CDE，即可得到CD＝FA，再根据CD∥AF，即可得出四边形ACDF是平行四边形．解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠FAE＝∠CDE，∵E是AD的中点，∴AE＝DE，又∵∠FEA＝∠CED，∴△FAE≌△CDE(ASA)，∴CD＝FA，又∵CD∥AF，∴四边形ACDF是平行四边形
【对应训练】7．如图，将一张直角三角形纸片ABC沿中位线DE剪开后，在平面上将△BDE绕着CB的中点D逆时针旋转180°，点E到了点E′的位置，则四边形ACE′E的形状是______________．
8．如图，已知点E，C在线段BF上，BE＝CE＝CF，AB∥DE，∠ACB＝∠F.(1)求证：△ABC≌△DEF；(2)试判断四边形AECD的形状，并证明你的结论．解：(1)∵AB∥DE，∴∠B＝∠DEF，∵BE＝EC＝CF，∴BC＝EF，又∵∠ACB＝∠F，∴△ABC≌△DEF(ASA)　(2)四边形AECD是平行四边形．证明：∵△ABC≌△DEF，∴AC＝DF，∵∠ACB＝∠F，∴AC∥DF，∴四边形ACFD是平行四边形，∴AD∥CF，AD＝CF，∵EC＝CF，∴AD∥EC，AD＝CE，∴四边形AECD是平行四边形
9．如图1，在▱ABCD中，点O是对角线AC的中点，EF过点O与AD，BC分别相交于点E，F，GH过点O与AB，CD分别相交于点G，H，连接EG，FG，FH，EH.(1)求证：四边形EGFH是平行四边形；(2)如图2，若EF∥AB，GH∥BC，在不添加任何辅助线的情况下，请直接写出图2中与四边形AGHD面积相等的所有的平行四边形．(四边形AGHD除外)
解：(1)∵四边形ABCD为平行四边形，∴AD∥BC，∴∠EAO＝∠FCO，又∵OA＝OC，∠AOE＝∠COF，∴△OAE≌△OCF(ASA)，∴OE＝OF，同理OG＝OH，∴四边形EGFH是平行四边形(2)▱GBCH，▱ABFE，▱EFCD，▱EGFH
10．(巴中中考)如图，在▱ABCD中，过B点作BM⊥AC于点E，交CD于点M，过D点作DN⊥AC于点F，交AB于点N.(1)求证：四边形BMDN是平行四边形；(2)已知AF＝12，EM＝5，求AN的长．