人教版八年级下册第十八章 平行四边形综合与测试精品ppt课件

这是一份人教版八年级下册第十八章 平行四边形综合与测试精品ppt课件，共19页。

一、矩形的性质与判定【例1】如图，在△ABC中，AB＝6，AC＝8，BC＝10，P为边BC上一动点(且点P不与点B，C重合)，PE⊥AB于点E，PF⊥AC于点F，则EF的最小值为_____．分析：连接AP，由题中条件可证四边形AEPF为矩形，从中可得AP＝EF，只要求出AP的最小值即可，当AP⊥BC时，AP取得最小值．
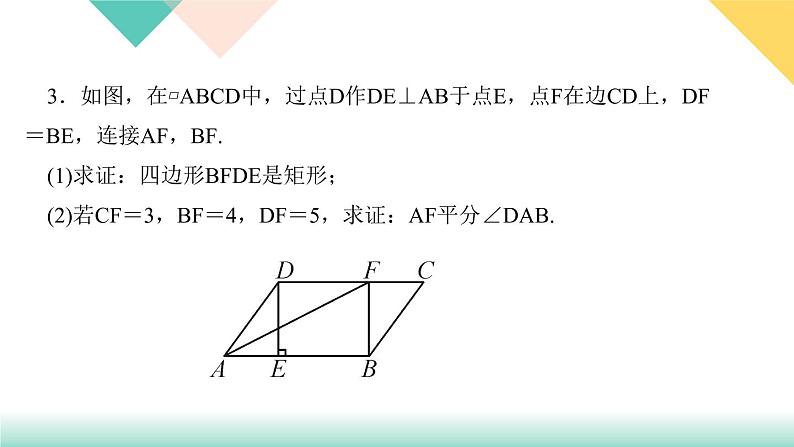
3．如图，在▱ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF.(1)求证：四边形BFDE是矩形；(2)若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB.
解：(1)在▱ABCD中，AB∥CD，∵DF＝BE，∴四边形BFDE为平行四边形，∵DE⊥AB，∴∠DEB＝90°，∴四边形BFDE是矩形　(2)由(1)可得∠BFC＝90°，在Rt△BFC中，由勾股定理可得BC＝5，∴AD＝BC＝5，∴AD＝DF，∴∠DAF＝∠DFA，∵AB∥CD，∴∠DFA＝∠FAB，∴∠DAF＝∠FAB，∴AF平分∠DAB
二、菱形的性质与判定【例2】如图，平行四边形ABCD的两条对角线相交于点O，E是BO的中点，过点B作AC的平行线，交CE的延长线于点F，连接AF.(1)求证：FB＝AO；(2)当平行四边形ABCD满足什么条件时，四边形AFBO是菱形？证明你的结论．分析：(1)可通过证△BEF≌△OEC及利用平行四边形的性质得证；(2)欲得到菱形AFBO，则必须有条件AO＝BO，此时▱ABCD所满足的条件即可确定.
解：(1)∵BF∥AC，∴∠BFE＝∠OCE，又∵BE＝OE，∠BEF＝∠OEC，∴△BEF≌△OEC(AAS)，∴BF＝OC，又∵OC＝OA，∴BF＝OA(2)当平行四边形ABCD是矩形时，四边形AFBO是菱形．理由：∵FB∥AO，且FB＝OA，∴四边形AFBO是平行四边形，∵平行四边形ABCD是矩形，∴OA＝OB，∴四边形AFBO是菱形
【对应训练】4．把一个长方形的纸片按如图所示折两次，然后剪下一部分，为了得到一个钝角为120°的菱形，剪口与第二次折痕所成角的度数应为( )A．15°或30° B．30°或45°C．45°或60° D．30°或60°
6．如图，在边长为10的菱形ABCD中，对角线BD＝16，点O是直线BD上的动点，OE⊥AB于点E，OF⊥AD于点F.(1)对角线AC的长是____，菱形ABCD的面积是____；(2)如图①，当点O在对角线BD上运动时，OE＋OF的值是否会发生变化？请说明理由；(3)如图②，当点O在对角线BD的延长线上时，OE＋OF的值是否会发生变化？若不变，请说明理由；若变化，请探究OE，OF之间的数量关系，并说明理由．
三、正方形的性质与判定【例3】如图，P是矩形ABCD内一点，AP⊥BP于点P，CE⊥BP于点E，BP＝EC.(1)请判断四边形ABCD是否是正方形？若是，写出证明过程；若不是，说明理由；(2)延长EC到点F，使CF＝BE，连接PF交BC的延长线于点G，求∠BGP的度数．分析：(1)由AAS可证△ABP≌△BCE，可得AB＝BC，即可得出结论；(2)连接AC，由△ABP≌△BCE可得AP＝BE＝CF，可证四边形ACFP是平行四边形，从而由∠ACB＝∠BGP可得结果．
解：(1)四边形ABCD为正方形．证明：∵四边形ABCD是矩形，∴∠ABC＝90°，即∠ABP＋∠PBC＝90°，∵AP⊥BP，∴∠ABP＋∠PAB＝90°，∴∠PBC＝∠PAB，∵CE⊥BP，∴∠APB＝∠BEC＝90°，又∵BP＝CE，∴△ABP≌△BCE(AAS)，∴AB＝BC，∴矩形ABCD为正方形　(2)连接AC，∵△ABP≌△BCE，∴AP＝BE，∵BE＝CF，∴AP＝CF，∵AP⊥BP，CE⊥BP，∴AP∥CF，∴四边形ACFP是平行四边形，∴AC∥PF，∴∠ACB＝∠BGP，∵四边形ABCD是正方形，AC是对角线，∴∠ACB＝45°，∴∠BGP＝45°
【对应训练】7．(2019·绍兴)正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D.在点E从点A移动到点B的过程中，矩形ECFG的面积( )A．先变大后变小 B．先变小后变大C．一直变大 D．保持不变
8．如图①，在正方形ABCD中，P是BD上的一点，点E在AD延长线上，且PA＝PE，PE交CD于点F.(1)求证：PC＝PE；(2)求∠CPE的度数；(3)如图②，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC＝120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．