





初中数学人教版八年级下册第十七章 勾股定理综合与测试精品复习课件ppt
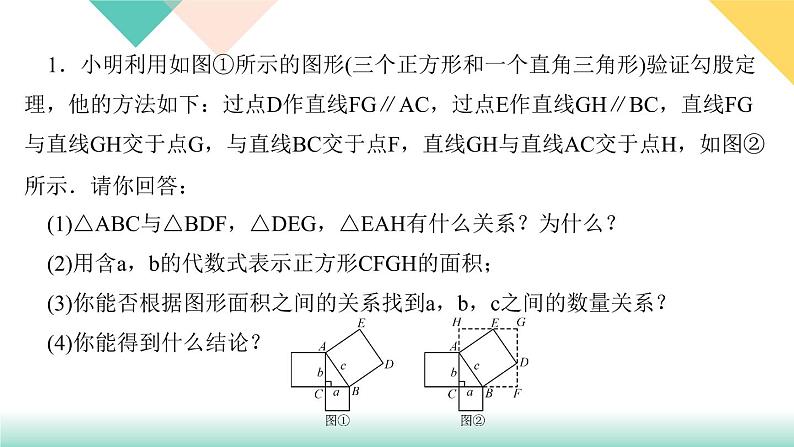
展开1.小明利用如图①所示的图形(三个正方形和一个直角三角形)验证勾股定理,他的方法如下:过点D作直线FG∥AC,过点E作直线GH∥BC,直线FG与直线GH交于点G,与直线BC交于点F,直线GH与直线AC交于点H,如图②所示.请你回答:(1)△ABC与△BDF,△DEG,△EAH有什么关系?为什么?(2)用含a,b的代数式表示正方形CFGH的面积;(3)你能否根据图形面积之间的关系找到a,b,c之间的数量关系?(4)你能得到什么结论?
解:(1)△ABC≌△BDF≌△DEG≌△EAH.理由如下:因为∠BAC+∠ABC=90°,而∠ABC+∠DBF=90°,所以∠BAC=∠DBF.因为FG∥AC,所以BC⊥FG,即∠BFD=∠ACB=90°.又因为AB=BD,所以△ABC≌△BDF.同理,可得△ABC≌△DEG≌△EAH (2)(a+b)2 (3)能,a2+b2=c2 (4)在直角三角形中,两条直角边的平方和等于斜边的平方
2.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明灵感,他惊喜地发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.(请你写出证明过程)
3.等腰三角形的底边长为6,底边上的中线长为4,则它的腰长为( )A.7 B.6 C.5 D.44.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1,S2,S3.若正方形EFGH的边长为2,则S1+S2+S3=____.
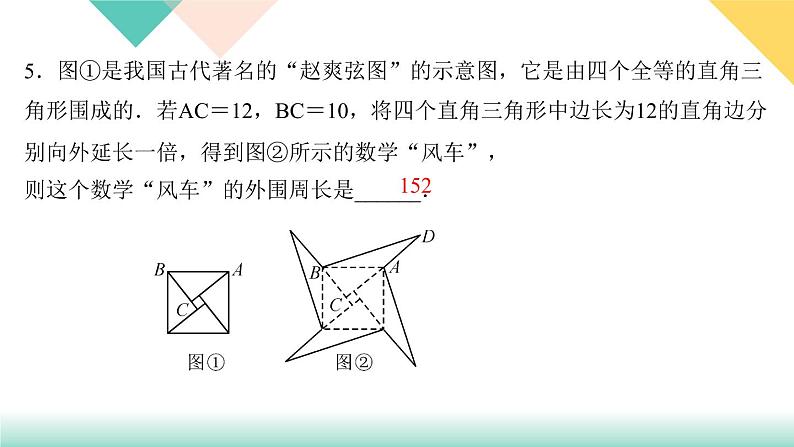
5.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=12,BC=10,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到图②所示的数学“风车”,则这个数学“风车”的外围周长是______.
7.在△ABC中,AB=13,AC=20,D是直线BC上的一个动点,连接AD,如果线段AD的长度最短是12,请你求△ABC的面积.
9.如果△ABC的三边长分别是m2-1,m2+1,2m(m>1),那么下列说法中正确的是( )A.△ABC是直角三角形,且斜边长为m2+1B.△ABC是直角三角形,且斜边长为2mC.△ABC是直角三角形,且斜边长为m2-1D.△ABC不是直角三角形
10.若a,b,c为△ABC的三边长,且a,b,c满足等式(a-5)2+(b-12)2+(c-13)2=0.(1)求a,b,c的值;(2)△ABC是直角三角形吗?请说明理由.解:(1)由题意得a-5=0,b-12=0,c-13=0,∴a=5,b=12,c=13 (2)△ABC是直角三角形.理由如下:∵a2+b2=52+122=25+144=169,c2=132=169,即a2+b2=c2,∴△ABC是直角三角形
11.如图,E是正方形ABCD内的一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=_____°.
12.如图,在4×3的长方形网格中有从点A出发的四条线段AB,AC,AD,AE,它们的另一个端点B,C,D,E均在格点上(正方形网格的交点).(1)若每个正方形的边长都是1,分别求出AB,AC,AD,AE的长度(结果可以保留根号);(2)在AB,AC,AD,AE四条线段中,是否存在三条线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
14.如图,A,B两地之间有一座山,汽车原来从A地到B地需经过C地沿折线ACB行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)
初中数学人教版八年级下册第十七章 勾股定理综合与测试复习ppt课件: 这是一份初中数学人教版八年级下册第十七章 勾股定理综合与测试复习ppt课件,共16页。PPT课件主要包含了勾股定理,勾股定理的逆定理,X+1米,解得X3,∵AB⊥BC,∴EC3,AB≈3米,仔细想想喔,你有收获吗,∵AD⊥BC等内容,欢迎下载使用。
数学九年级下册第二十七章 相似综合与测试复习ppt课件: 这是一份数学九年级下册第二十七章 相似综合与测试复习ppt课件,共22页。PPT课件主要包含了①③④等内容,欢迎下载使用。
人教版八年级下册第十七章 勾股定理综合与测试公开课ppt课件: 这是一份人教版八年级下册第十七章 勾股定理综合与测试公开课ppt课件,共18页。













