

初中数学第十八章 平行四边形综合与测试优秀单元测试课时作业
展开(满分120分 时间90分钟)
一.选择题(共10小题,满分30分,每小题3分)
1.菱形具有而平行四边形不具有的性质是( )
A.对角线互相垂直B.两组对角分别相等
C.对角线互相平分D.两组对边分别平行
2.在▱ABCD中,∠A:∠B:∠C:∠D可能是( )
A.1:2:3:4B.2:3:2:3C.2:2:1:1D.2:3:3:2
3.一个三角形的三条中位线的长为6、7、8,则此三角形的周长为( )
A.10.5B.21C.42D.63
4.如图,在四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BCB.AB=DC,AD=BC
C.AD∥BC,AB=DCD.AB∥DC,AB=DC
5.在Rt△ABC中,D为斜边AB的中点,且BC=3,AC=4,则线段CD的长是( )
A.2B.3C.D.5
6.如图,在▱ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是( )
A.B.2C.D.3
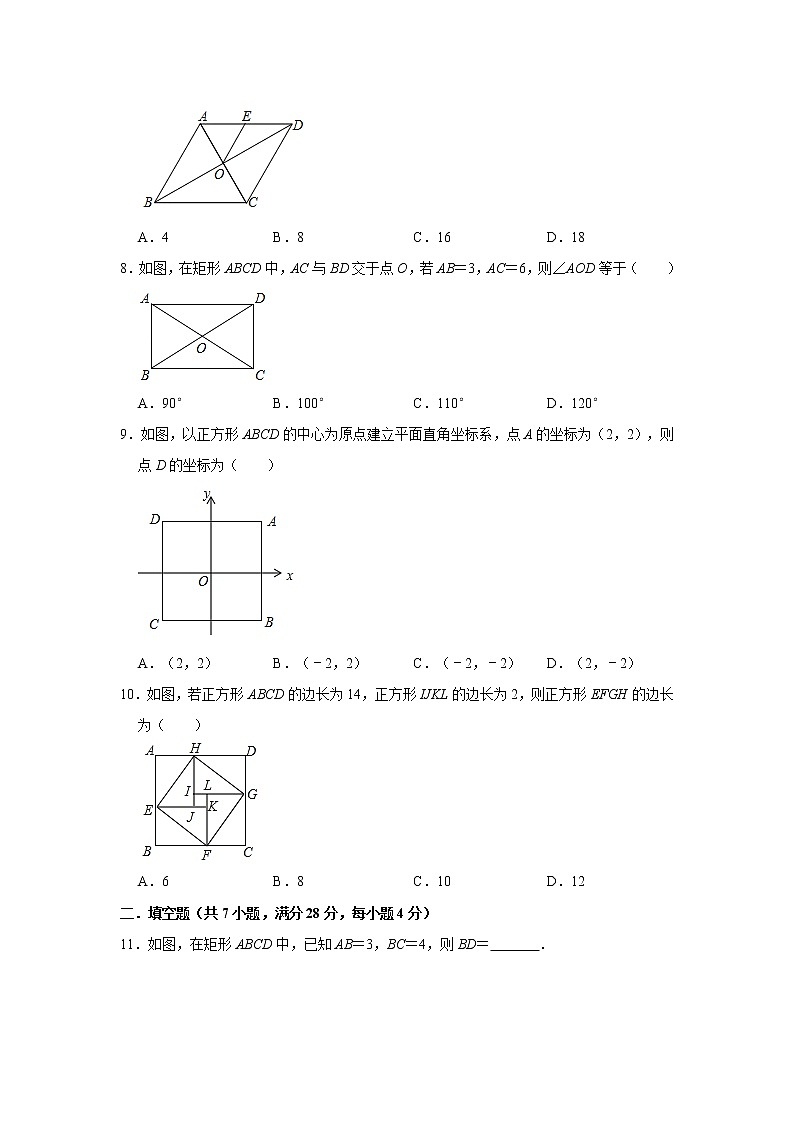
7.如图,菱形ABCD中,对角线AC,BD相交于点O,E是AD边的中点,菱形ABCD的周长为32,则OE的长等于( )
A.4B.8C.16D.18
8.如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )
A.90°B.100°C.110°D.120°
9.如图,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(2,2),则点D的坐标为( )
A.(2,2)B.(﹣2,2)C.(﹣2,﹣2)D.(2,﹣2)
10.如图,若正方形ABCD的边长为14,正方形IJKL的边长为2,则正方形EFGH的边长为( )
A.6B.8C.10D.12
二.填空题(共7小题,满分28分,每小题4分)
11.如图,在矩形ABCD中,已知AB=3,BC=4,则BD= .
12.如图,在平行四边形ABCD中,添加一个条件 使平行四边形ABCD是菱形.
13.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD= cm.
14.如图,在正方形ABCD的外侧,作等边三角形ABE,则∠DEB的度数为 度.
15.在▱ABCD中,AB=8,BC=10,∠B=30°,则▱ABCD的面积为 .
16.在平面直角坐标系中,O为坐标系原点,A(﹣3,0)、B(﹣5,2)、C在坐标平面内,若以O、A、B、C为顶点的四边形是平行四边形,则点C坐标为 .
17.如图,在矩形ABCD中,AB=6,AD=8,以A为圆心,任意长为半径画弧交AB,AC于M,N,再分别以M,N为圆心,大于MN为半径画弧,两弧交于点G,连接AG,交边BC于E,则△AEC的面积为 .
三.解答题(共8小题,具体分值在题号后,满分62分)
18.(6分)如图,将▱ABCD的对角线BD向两个方向延长,分别至点E和点F,BE=DF.求证:四边形AECF是平行四边形.
19.(6分)已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
20.(6分)如图,在正方形ABCD中,点E、F分别是AB、BC上的点,且AE=BF.求证:AF⊥DE.
21.(8分)如图,菱形ABCD中,对角线AC、BD交于点O,AC=24,BD=10,DE⊥AB于E.
(1)求菱形ABCD的周长;
(2)求菱形ABCD的面积;
(3)求DE的长.
22.(8分)正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
23.(8分)如图,在矩形ABCD中,过BD的中点O作EF⊥BD,分别与AB、CD交于点E、F.连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若M是AD中点,联结OM与DE交于点N,AD=OM=4,则ON的长是多少?
24.(10分)在▱ABCD中,点E,F分别是BC,CD上的点,且DF=CF,连接AE,AF,并延长AF交BC的延长线于点P.
(1)求证:△ADF≌△PCF;
(2)若AE=2,AF=4,∠EAF=60°,求PE的长.
25.(10分)如图,长方形ABCD中,AB∥CD,∠D=90°,AB=CD,AD=4cm,点P从点D出发(不含点D)以2cm/s的速度沿D→A→B的方向运动到点B停止,点P出发1s后,点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止,当点P到达点B时,点Q恰好到达点D.
(1)当点P到达点A时,△CPQ的面积为3cm2,求CD的长;
(2)在(1)的条件下,设点P运动时间为t(s),运动过程中△BPQ的面积为S(cm2),请用含t(s)的式子表示面积S(cm2),并直接写出t的取值范围.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、正确.对角线互相垂直是菱形具有而平行四边形不具有的性质;
B、错误.两组对角分别相等,是菱形和平行四边形都具有的性质;
C、错误.对角线互相平分,是菱形和平行四边形都具有的性质;
D、错误.两组对边分别平行,是菱形和平行四边形都具有的性质;
选:A.
2.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴∠A:∠B:∠C:∠D可能是2:3:2:3;
选:B.
3.解:∵三角形的三条中位线的长为6、7、8,
∴三角形的三边长分别为12、14、16,
∴此三角形的周长=12+14+16=42,
选:C.
4.解:平行四边形的判定条件:
1、两组对边分别平行的四边形是平行四边形(定义判定法);即选项A;
2、一组对边平行且相等的四边形是平行四边形;即选项D;
3、两组对边分别相等的四边形是平行四边形;即选项B
选:C.
5.解:∵AC=4cm,BC=3,
∴AB==5,
∵D为斜边AB的中点,
∴CD=AB=×5=.
选:C.
6.解:∵四边形ABCD为平行四边形,
∴AB∥CD,CD=AB=6,
∴∠ABE=∠CEB,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠CEB,
∴CE=BC=4,
∴DE=CD﹣CE=6﹣4=2.
选:B.
7.解:∵菱形ABCD的周长为32,
∴AB=8,
∵E为AD边中点,O为BD的中点
∴OE=AB=4.
选:A.
8.解:∵在矩形ABCD中,AC与BD交于点O,AC=6,
∴OA=OB=AC=3,
∵AB=3,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠AOD=180°﹣∠AOB=120°.
选:D.
9.解:如图所示:∵以正方形ABCD的中心O为原点建立坐标系,点A的坐标为(2,2),
∴点B、C、D的坐标分别为:(2,﹣2),(﹣2,﹣2),(﹣2,2).
选:B.
10.解:由图可得,S△AEH+S△BFE+S△CGF+S△DHG=S△HJE+S△EKF+S△FLG+S△GIH,
设S△AEH+S△BFE+S△CGF+S△DHG=S△HJE+S△EKF+S△FLG+S△GIH=x,
则S正方形EFGH=S正方形ABCD﹣x=S正方形IJKL+x,
即196﹣x=4+x,
解得x=96,
∴S正方形EFGH=196﹣96=100,
∴正方形EFGH的边长为10,
选:C.
二.填空题(共7小题,满分28分,每小题4分)
11.解:由勾股定理可知,
答案为5.
12.解:当AB=BC或AC⊥BD时,四边形ABCD是菱形.
答案为AB=BC或AC⊥BD.
13.解:∵平行四边形的周长为20cm,
∴AB+BC=10cm;
又△BOC的周长比△AOB的周长大2cm,
∴BC﹣AB=2cm,
解得:AB=4cm,BC=6cm.
∵AB=CD,
∴CD=4cm
答案为:4.
14.解:∵四边形ABCD是正方形
∴AB=AD,∠BAD=90°
∵△ABE是等边三角形
∴AE=AB,∠BAE=∠BEA=60°
∴AD=AE,∠DAE=150°
∴∠AED=∠ADE=(180°﹣∠DAE)=15°
∴∠DEB=∠BEA﹣∠AED=60°﹣15°=45°
答案为:45.
15.解:如图所示:过点A作AH⊥BC于点H,
∵AB=8,∠B=30°,
∴AH=AB=4,
∴▱ABCD的面积为:AH•BC=4×10=40.
答案为:40.
16.解:如图所示:
∵A(﹣3,0),
∴OA=3,
①当四边形OACB是平行四边形时,BC=OA=3,
∵B(﹣5,2),
∴C(﹣2,2),
②当四边形OABC′是平行四边形时,BC'=OA=3,
∵B(﹣5,2),
∴C(﹣8,2);
③当四边形OBAC′'是平行四边形时,
∵A(﹣3,0),B(﹣5,2),
∴C(2,﹣2),
答案为:(﹣2,2)或(﹣8,2)或(2,﹣2).
17.解:作EF⊥AC于F,如图:
由题意得:AE平分∠BAC,
∵四边形ABCD是矩形,
∴∠B=90°,BC=AD=8,
∴AC===10,
EB⊥AB,
∵AE平分∠BAC,
∴EF=EB,
在Rt△AEF和Rt△AEB中,,
∴Rt△AEF≌Rt△AEB(HL),
∴AF=AB=6,
∴CF=AC﹣AF=4,
设EF=EB=x,则CE=8﹣x,
在Rt△CEF中,由勾股定理得:x2+42=(8﹣x)2,
解得:x=3,
∴EF=3,
∴△AEC的面积=AC×EF=×10×3=15;
答案为:15.
三.解答题(共8小题,具体分值在题号后,满分62分)
18.证明:连接AC,设AC与BD交于点O.如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵BE=DF,
∴OE=OF.
∴四边形AECF是平行四边形.
19.证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE∥AD,
∴∠AEC=90°,
∴四边形ADCE为矩形.
20.证明:∵四边形ABCD为正方形,
∴DA=AB,∠DAE=∠ABF=90°,
在△DAE和△ABF中
,
∴△DAE≌△ABF(SAS),
∴∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠FAE+∠AED=90°,
∴∠AGE=90°,
∴AF⊥DE.
21.解:(1)解:∵菱形ABCD中,BD=10,AC=24,
∴OB=5,OA=12,
在Rt△ABO中,AB==13,
∴菱形ABCD的周长=4AB=52.
(2)S菱形ABCD=•AC•BD=×24×10=120.
(3)∵S菱形ABCD=•AC•BD=AB•DE,
∴DE=.
22.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF,
∴EF=CF+AE;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
23.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DFO=∠BEO,
∵∠DOF=∠EOB,OD=OB,
∴△DOF≌△BOE(AAS),
∴DF=BE,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形.
(2)解:∵DM=AM,DO=OB,
∴OM∥AB,AB=2OM=8,
∴DN=EN,ON=BE,设DE=EB=x,
在Rt△ADE中,则有x2=42+(8﹣x)2,
解得x=5,
∴ON=.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠PCF,
在△ADF和△PCF中,,
∴△ADF≌△PCF(ASA);
(2)解:作EM⊥AP于M,如图所示:
∵∠EAF=60°,
∴∠AEM=90°﹣60°=30°,
∴AM=AE=1,
∴EM=AM=,
由(1)得:△ADF≌△PCF,
∴PF=AF=4,
∴AP=8,
∴PM=AP﹣AM=7,
∴PE===2.
25.解:(1)设点P运动时间为t(s),根据题意,得
点P出发1s后,点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止,
当点P到达点B时,点Q恰好到达点D.
∴2(t﹣2)=a(t﹣1),
当点P到达点A时,△CPQ的面积为3cm2,
即a×1×4=3,
∴a=.
即2(t﹣2)=(t﹣1),
解得t=5,
所以CD=a(t﹣1)=6.
答:CD的长为6;
(2)根据题意,得
BC=AD=4,CD=6
DP=2t,CQ=1.5(t﹣1),
①点P的运动时间为t,0﹣1秒时点Q还在点C,
△BPQ面积不变为=12;
即S=12(0<t<1)
②当1<t<2时,
DQ=6﹣1.5(t﹣1)=7.5﹣1.5t,
S=S梯形DPBC﹣S△DPQ﹣S△BQC
=(2t+4)×6﹣×2t×(7.5﹣1.5t)﹣×1.5(t﹣1)×4
=1.5t2﹣4.5t+15;
③当2<t<5时,
BP=10﹣2t,
S=BP•BC
=(10﹣2t)×4
=20﹣4t.
综上所述:
运动过程中△BPQ的面积为S(cm2),
用含t(s)的式子表示面积S(cm2)为:
S=12 (0<t<1)
或S=1.5t2﹣4.5t+15(1<t<2)
或S=20﹣4t(2<t<5).
初中数学人教版八年级下册第十八章 平行四边形综合与测试精品单元测试课时训练: 这是一份初中数学人教版八年级下册第十八章 平行四边形综合与测试精品单元测试课时训练,共19页。试卷主要包含了选择题,填空题,计算题等内容,欢迎下载使用。
2021学年第十八章 平行四边形综合与测试单元测试达标测试: 这是一份2021学年第十八章 平行四边形综合与测试单元测试达标测试,文件包含第18章重点突破训练平行四边形类型题举例-解析版docx、第18章平行四边形单元测试卷-解析版docx、第18章重点突破训练平行四边形类型题举例-原卷版docx、第18章平行四边形单元测试卷-原卷版docx等4份试卷配套教学资源,其中试卷共140页, 欢迎下载使用。
人教版八年级下册第十八章 平行四边形综合与测试测试题: 这是一份人教版八年级下册第十八章 平行四边形综合与测试测试题,共31页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













