


























20.2021年高考数学(理)总复习(高考研究课件 高考达标检测 教师用书)第二单元 函数的概念及其性质 (6份打包)
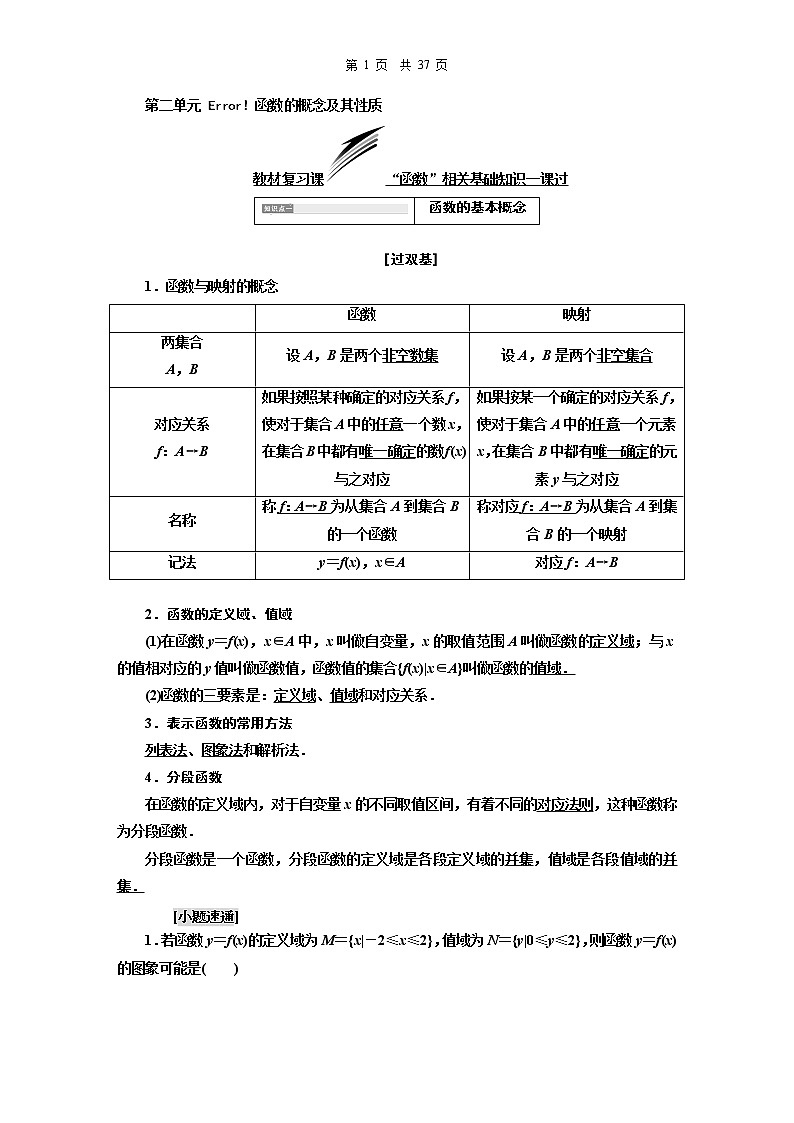
展开高考达标检测(四) 函数的定义域、解析式及分段函数一、选择题1.(2016·广东模拟)设函数f(x)满足f =1+x,则f(x)的表达式为( )A. B.C. D.解析:选A 令=t,则x=,代入f =1+x,得f(t)=1+=,即f(x)=,故选A.2.(2017·惠州调研)已知函数f(x)的定义域为[0,2],则g(x)=的定义域为( )A.[0,1)∪(1,2] B.[0,1)∪(1,4]C.[0,1) D.(1,4]解析:选C 由题意可知,解得0≤x<1,故g(x)=的定义域为[0,1),选C.3.(2017·福建调研)设函数f:R→R满足f(0)=1,且对任意x,y∈R都有f(xy+1)=f(x)f(y)-f(y)-x+2,则f(2 017)=( )A.0 B.1C.2 017 D.2 018解析:选D 令x=y=0,则f(1)=f(0)f(0)-f(0)-0+2=1×1-1-0+2=2,令y=0,则f(1)=f(x)f(0)-f(0)-x+2,将f(0)=1,f(1)=2代入,可得f(x)=1+x,所以f(2 017)= 2 018.故选D.4.若f(x)对于任意实数x恒有2f(x)-f(-x)=3x+1,则f(1)=( )A.2 B.0C.1 D.-1解析:选A 令x=1,得2f(1)-f(-1)=4,①令x=-1,得2f(-1)-f(1)=-2, ②联立①②得f(1)=2.5.若二次函数g(x)满足g(1)=1,g(-1)=5,且图象过原点,则g(x)的解析式为( )A.g(x)=2x2-3x B.g(x)=3x2-2xC.g(x)=3x2+2x D.g(x)=-3x2-2x解析:选B 设g(x)=ax2+bx+c(a≠0),∵g(1)=1,g(-1)=5,且图象过原点,∴解得∴g(x)=3x2-2x.6.(2017·青岛模拟)已知函数f(x)=则使f(x)=2的x的集合是( )A. B.C. D.解析:选A 由题意可知,f(x)=2,即或解得x=或4,故选A.7.(2017·莱芜模拟)已知函数f(x)的定义域为[3,6],则函数y=的定义域为( )A. B.C. D.解析:选B 要使函数y=有意义,需满足⇒⇒≤x<2.故选B.8.(2017·武汉调研)函数f(x)=满足f(1)+f(a)=2,则a的所有可能取值为( )A.1或- B.-C.1 D.1或解析:选A ∵f(1)=e1-1=1且f(1)+f(a)=2,∴f(a)=1,当-1<a<0时,f(a)=sin(πa2)=1,∵0<a2<1,∴0<πa2<π,∴πa2=⇒a=-;当a≥0时,f(a)=ea-1=1⇒a=1.故a=-或1.二、填空题9.已知函数y=f(x2-1)的定义域为[-,],则函数y=f(x)的定义域为________.解析:∵y=f(x2-1)的定义域为[-,],∴x∈[-, ],x2-1∈[-1,2],∴y=f(x)的定义域为[-1,2].答案:[-1,2]10.(2017·杭州模拟)已知f(x)=使f(x)≥-1成立的x的取值范围是________.解析:由题意知或解得-4≤x≤0或0<x≤2,故x的取值范围是[-4,2].答案:[-4,2]11.具有性质:f =-f(x)的函数,我们称为满足“倒负”变换的函数.下列函数:①y=x-;②y=x+;③y=其中满足“倒负”变换的函数是________.(填序号)解析:对于①,f(x)=x-,f =-x=-f(x),满足题意;对于②,f =+x=f(x)≠-f(x),不满足题意;对于③,f =即f =故f =-f(x),满足题意.答案:①③12.(2016·北京高考)设函数f(x)=①若a=0,则f(x)的最大值为________;②若f(x)无最大值,则实数a的取值范围是________.解析:当x≤a时,由f′(x)=3x2-3=0,得x=±1.如图是函数y=x3-3x与y=-2x在没有限制条件时的图象.①若a=0,则f(x)max=f(-1)=2.②当a≥-1时,f(x)有最大值;当a<-1时,y=-2x在x>a时无最大值,且-2a>(x3-3x)max,所以a<-1.答案:①2 ②(-∞,-1)三、解答题13.已知f(x)=x2-1,g(x)=(1)求f(g(2))与g(f(2));(2)求f(g(x))与g(f(x))的表达式.解:(1)由已知,g(2)=1,f(2)=3,因此f(g(2))=f(1)=0,g(f(2))=g(3)=2.(2)当x>0时,g(x)=x-1,故f(g(x))=(x-1)2-1=x2-2x;当x<0时,g(x)=2-x,故f(g(x))=(2-x)2-1=x2-4x+3.所以f(g(x))=当x>1或x<-1时,f(x)>0,故g(f(x))=f(x)-1=x2-2;当-1<x<1时,f(x)<0,故g(f(x))=2-f(x)=3-x2.所以g(f(x))=14.行驶中的汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离.在某种路面上,某种型号汽车的刹车距离y(米)与汽车的车速x(千米/时)满足下列关系:y=+mx+n(m,n是常数).如图是根据多次实验数据绘制的刹车距离y(米)与汽车的车速x(千米/时)的关系图.(1)求出y关于x的函数表达式;(2)如果要求刹车距离不超过25.2米,求行驶的最大速度.解:(1)由题意及题图,得解得m=,n=0,所以y=+(x≥0).(2)令+≤25.2,得-72≤x≤70.∵x≥0,∴0≤x≤70.故行驶的最大速度是70千米/时.





