初中数学北师大版八年级下册2 直角三角形优质课件ppt

这是一份初中数学北师大版八年级下册2 直角三角形优质课件ppt，共39页。PPT课件主要包含了两边的平方和，第三边的平方，逆命题，真命题，逆定理，△BCD是直角三角形，教你解题等内容，欢迎下载使用。

1.进一步掌握推理证明的方法,发展演绎推理能力.(重点)2.了解勾股定理及其逆定理的证明方法.(重点)3.结合具体例子了解逆命题的概念,会识别两个互逆命题,知道原命题成立其逆命题不一定成立.(难点)
一、直角三角形的性质1.定理:直角三角形的两个锐角互余.2.勾股定理:直角三角形两条直角边的平方和等于斜边的平方.二、直角三角形的判定1.定理:有两个角互余的三角形是直角三角形.
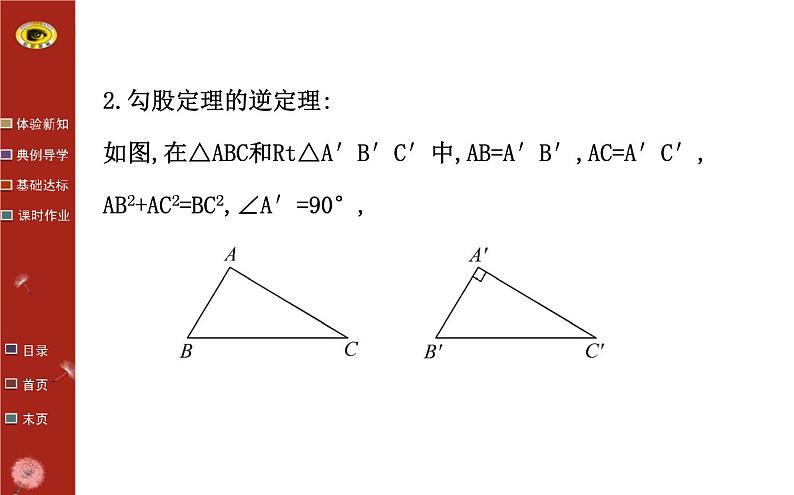
2.勾股定理的逆定理:如图,在△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,AB2+AC2=BC2,∠A′=90°,
【思考】(1)BC与B′C′相等吗?为什么?提示:BC=B′C′,理由如下:在Rt△A′B′C′中,由勾股定理得A′B′2+A′C′2=B′C′2,∵AB=A′B′,AC=A′C′,AB2+AC2=BC2,∴BC2=B′C′2,∴BC=B′C′.
(2)请求出∠A的度数.提示:由(1)知BC=B′C′,又∵AB=A′B′,AC=A′C′,∴△ABC≌△A′B′C′(SSS),∴∠A=∠A′=90°.
【总结】勾股定理逆定理:如果三角形_____________等于_____________,那么这个三角形是直角三角形.
三、互逆命题、互逆定理1.互逆命题:在两个命题中,如果一个命题的条件和_____分别是另一个命题的_____和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的_______.2.互逆定理:如果一个定理的逆命题经过证明是_______,那么它也是一个定理,这两个定理称为互逆定理.其中一个定理称为另一个定理的_______.
(1)边长分别为3,5,6的三角形是直角三角形.　( )(2)一个真命题的逆命题也是真命题.　( )(3)三边长为 , , 的三角形为直角三角形.　( )(4)定理“对顶角相等”的逆定理是“相等的角是对顶角”.　( )
知识点 1 勾股定理及其逆定理的应用 【例1】如图所示,在等腰△ABC中,底边BC=20,D为AB上一点,且CD=16,BD=12,求AC的长.
【解题探究】(1)因为△BCD的三边长已知,你能确定它的形状吗?提示:___,因为____________所以__________________.(2)△ACD是什么三角形?三边满足勾股定理吗?提示:____________________________________(3)设AD=x,则AC=_____.可得方程______________,解方程得x= ,所以得AC= .
122+162=202,
△ACD是直角三角形,三边满足勾股定理.
162+x2=(12+x)2
【互动探究】已知三角形的三边,能确定三角形的形状吗?提示:计算三边长的平方,看是否满足a2+b2=c2;如果满足,三角形为直角三角形,不满足,则不是直角三角形.
【总结提升】勾股定理及其逆定理的应用
知识点 2 互逆命题和互逆定理 【例2】已知命题:相反数的绝对值相等.(1)写出这个命题的逆命题.(2)判断逆命题的真假.
【总结提升】互逆命题和互逆定理中的“互换”和“包含”(1)互换:(2)包含:
题组一:勾股定理及其逆定理的应用1.(2013·安顺中考)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行　(　　)
A.8米　　　B.10米　　　C.12米　　　D.14米【解析】选B.作AB⊥BC于点B,连接AC,如图:根据题意可得:BC=10-4=6(米),AB=8米,所以AC==10(米).
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知BC=8,AC=6,则线段CD的长为　(　　)【解析】选C.∵∠ACB=90°,BC=8,AC=6,∴AB=10.∵CD⊥AB,∴ AB·CD= AC·BC,即 ×10×CD= ×8×6,∴CD= .
3.有一木匠师傅测量一个等腰三角形的腰、底边和底边上的高的长,但是他把这三个数据和其他数据弄混了.请你帮他找出来,它们是　(　　)A.13,12,12　　B.12,12,8　　C.13,10,12　　　　D.5,8,4【解析】选C.因为等腰三角形底边上的高平分底边,所以腰、底边的一半、高满足c2=a2+b2,即132= +122.
4.(2013·莆田中考)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为2,5,1,2.则最大的正方形E的面积是　　　　.
【解析】设中间两个正方形的边长分别为x,y,最大正方形E的边长为z,则由勾股定理得:x2=2+5=7,y2=2+1=3,z2=x2+y2=10,即最大正方形E的面积为z2=10.答案:10
5.已知三角形的三边之比是5∶12∶13,如果它的周长是60cm,则它的面积是　　　　cm2.【解析】设三角形的三边分别是5xcm,12xcm,13xcm,则根据题意得,5x+12x+13x=60,解得x=2,故三角形三边分别是10,24,26.又因102+242=262,所以三角形为直角三角形,面积为 ×10×24=120(cm2).答案:120
6.如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=　　　　.
【解析】设B点的对应点为B′.连接DB′,由勾股定理得AC=5,又AB′=AB,所以B′C=5-3=2,设DB=DB′=x,则DC=4-x,在Rt△DB′C中,利用勾股定理得x2+22=(4-x)2,解得x= ,即BD= .答案:
【归纳整合】勾股定理主要用来求三角形的边长,只要知道直角三角形的两条边,就可以求出它的第三条边,当我们只知道直角三角形的一条边时,如果我们可以找到另外两边的关系,也可以通过列方程(组)的方法求出另外两条边.若未指明哪条边是直角边或斜边时,要分类讨论防止漏解.
7.有一块空白地,∠ADC=90°,CD=6m,AD=8m,AB=26m,BC=24m,现计划在该空地上进行绿化,若平均每平方米投资100元,那么该空白地绿化需要投资多少元?
【解析】连接AC,得直角△ACD.所以根据勾股定理得AC2=AD2+CD2=82+62=102,即AC=10米.又因102+242=262即AC2+CB2=AB2,所以△ABC是直角三角形,所以S空白地=S△ABC-S△ACD= ×10×24- ×6×8=96(m2).96×100=9600(元).答:该空白地绿化需要投资9600元.
题组二:互逆命题和互逆定理1.下列命题的逆命题是真命题的是　(　　)A.若a=b,则a2=b2B.全等三角形的周长相等C.若a=0,则ab=0D.直角三角形的两个锐角互余
【解析】选D.A的逆命题是“若a2=b2,则a=b”,是假命题;B的逆命题是“周长相等的三角形是全等三角形”,是假命题;C的逆命题是“若ab=0,则a=0”,是假命题;D的逆命题是“两锐角互余的三角形为直角三角形”,是真命题.
2.已知下列命题:①若a≤0,则|a|=-a;　　②若ma2>na2,则m>n;③两组对角分别相等的四边形是平行四边形.其中原命题与逆命题均为真命题的个数是　(　　)A.0个 B.1个 C.2个 D.3个
【解析】选C.三个命题的原命题均为真命题,①的逆命题为:若|a|=-a,则a≤0,也为真命题;②的逆命题为:若m>n,则ma2>na2,当a=0时,结论不成立,是假命题;③的逆命题是平行四边形的两组对角分别相等,是真命题.综上可知原命题和逆命题均为真命题的是①③,有2个.
【归纳整合】互逆命题和互逆定理的真假关系(1)互逆命题的真假没有必然的联系,它们的真假都必须经过说明论证或经过反例验证(假命题),原命题真,逆命题不一定真,原命题假,而逆命题不一定假.(2)因为一个定理的逆命题不一定是真命题,所以并不是所有的定理都有逆定理.
3.命题“平行四边形的对角线互相平分”的逆命题是　　　　.【解析】“平行四边形对角线互相平分”的条件是:四边形是平行四边形,结论是:四边形的对角线互相平分.所以逆命题是:对角线互相平分的四边形是平行四边形.答案:对角线互相平分的四边形是平行四边形
4.下列命题:①矩形的对角线相等;②和为180°的两个角互为补角;③两直线平行,同位角相等.其中逆命题为真命题的是　　　　.【解析】①的逆命题是“对角线相等的四边形是矩形”,是假命题;②的逆命题是“互为补角的两个角的和为180°”,是真命题;③的逆命题是“同位角相等,两直线平行”,是真命题.故逆命题为真命题的是②③.答案:②③
5.写出下列命题的逆命题,并判定真假.(1)如果x2=4,那么x=2.(2)全等三角形的面积相等.【解析】(1)如果x=2,那么x2=4,真命题.(2)面积相等的三角形是全等三角形,假命题.
【想一想错在哪？】在Rt△ABC中,BC=3,AB=4,求AC的长.提示:∠B和∠C都可能是直角,未分类讨论.
P18 习题1.5 1-5题