初中北师大版2 直角三角形试讲课ppt课件

这是一份初中北师大版2 直角三角形试讲课ppt课件，共25页。PPT课件主要包含了直角边，教你解题等内容，欢迎下载使用。

1.进一步掌握推理证明的方法,发展演绎推理能力.(重点)2.能够证明直角三角形全等的“HL”判定定理,并能根据“HL”定理解决实际问题.(重点、难点)
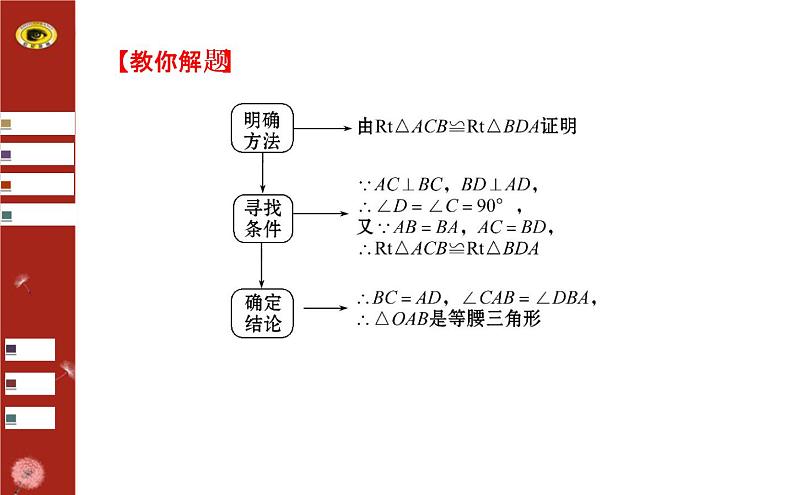
斜边、直角边定理的证明如图,在△ABC与△DEF中,∠A=∠D=90°,AB=DE,BC=EF.【思考】1.AC与DF相等吗?为什么?提示:AC=DF,理由如下:∵∠A=∠D=90°,根据勾股定理得AB2+AC2=BC2,DE2+DF2=EF2,又∵AB=DE,BC=EF,∴AC=DF.
2.△ABC与△DEF全等吗?为什么?提示:全等.∵AB=DE,BC=EF,AC=DF.∴△ABC≌△DEF(SSS).【总结】斜边、直角边定理:_____和一条_______分别相等的两个_____三角形全等,简称“斜边、直角边”定理,记作“___”.
(1)“HL”定理适合所有三角形全等的判定.　( )(2)一条直角边和一个锐角对应相等的两个直角三角形全等.　( )(3)有两条边对应相等的三角形全等.　( )(4)两个锐角对应相等的两个直角三角形全等.　( )(5)一锐角和斜边对应相等的两个直角三角形全等.　( )
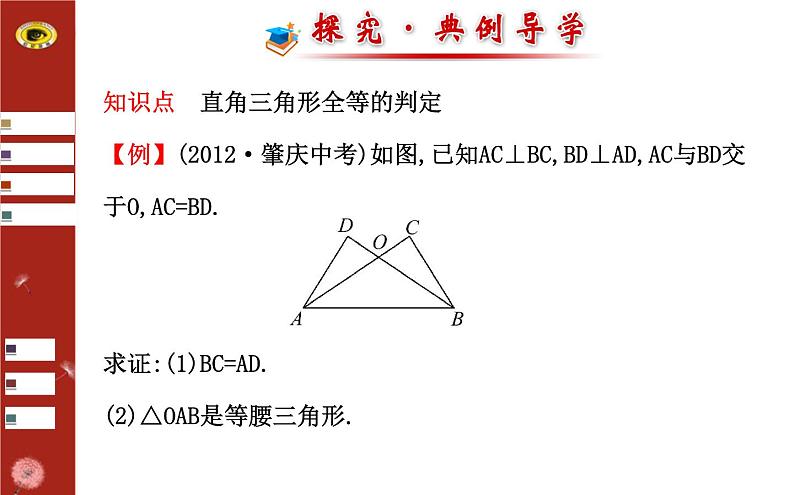
知识点 直角三角形全等的判定 【例】(2012·肇庆中考)如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:(1)BC=AD.(2)△OAB是等腰三角形.
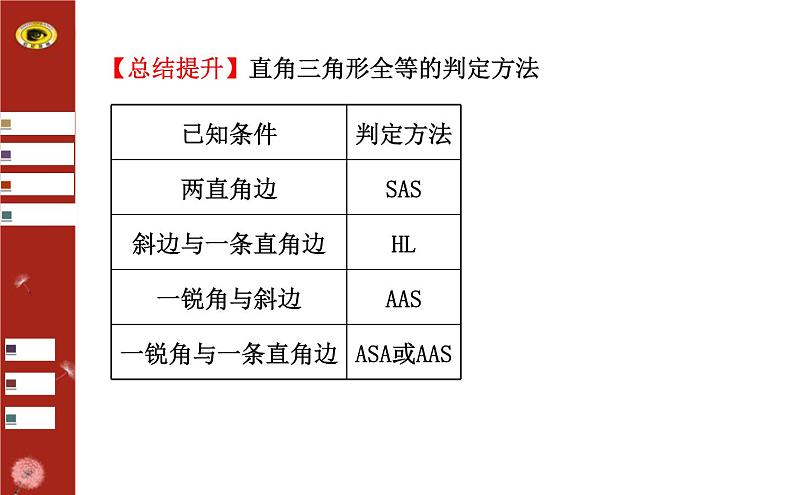
【总结提升】直角三角形全等的判定方法
题组:直角三角形全等的判定1.如图所示,AB⊥BC于点B,AD⊥DC于点D,若CB=CD,且∠1=30°,则∠BAD的度数是　(　　)A.90°　　　B.60°　　　C.30°　　　D.15°
【解析】选B.在Rt△ABC和Rt△ADC中,∵ ∴△ABC≌△ADC,∴∠1=∠CAD=30°,∴∠BAD=60°.
2.在下列条件中,不能判定两个直角三角形全等的是　(　　)A.两条直角边对应相等B.两个锐角对应相等C.一个锐角和一条直角边对应相等D.一条斜边和一条直角边对应相等【解析】选B.∵A符合“SAS”,C符合“AAS”或“ASA”,D满足“HL”,故A,C,D均能判定两个直角三角形全等,B项只满足“AAA”,不能判定两个三角形全等,故选B.
3.如图,AB=AC,AC≠BC,AH⊥BC于H,BD⊥AC于D,CE⊥AB于E,AH,BD,CE交于O,图中全等直角三角形的对数为　(　　)A.3B.4C.5D.6
【解析】选D.∵AB=AC,AC≠BC,AH⊥BC于H,BD⊥AC于D,CE⊥AB于E,∴BH=CH,∠BAH=∠CAH,∠ABC=∠ACB,BC=CB,AH=AH,∴Rt△ABH≌Rt△ACH,Rt△BCE≌Rt△CBD,∴BE=CD,∴AE=AD,∴Rt△AEO≌Rt△ADO,Rt△EOB≌Rt△DOC,Rt△ABD≌Rt△ACE,∴OB=OC,∴Rt△OHB≌Rt△OHC,∴共有6对全等直角三角形.
4.如图,AB⊥BE于B,DE⊥BE于E.(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是　　　　.(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是　　　　.(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是　　　　　.(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是　　　　　.
【解析】由AB⊥BE,DE⊥BE得∠ABC=∠DEF=90°,(1)∵∠A=∠D,AB=DE,根据ASA得△ABC≌△DEF.(2)∵∠A=∠D,BC=EF,根据AAS得△ABC≌△DEF.(3)∵AB=DE,BC=EF,根据SAS得△ABC≌△DEF.(4)∵AB=DE,AC=DF,根据HL得△ABC≌△DEF.答案:(1)ASA　(2)AAS　(3)SAS　(4)HL
5.如图,AB=AD,AD⊥DC,BC⊥AB,AC和BD相交于点E,则△ABC≌△　　　　,理由是　　　　;△ABE≌△　　　　,理由是　　　　.【解析】∵AB=AD,AC=AC,∴Rt△ABC≌Rt△ADC(HL),∴∠BAE=∠DAE,又∵AB=AD,AE=AE,∴△ABE≌△ADE(SAS).答案:ADC　HL　ADE　SAS
6.如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=　　　　.
【解析】∵MN∥PQ,AB⊥PQ,∴AB⊥MN,∴∠DAE=∠EBC=90°,在Rt△ADE和Rt△BEC中,∴Rt△ADE≌Rt△BEC(HL),∴AE=BC,∵AD+BC=7,∴AB=AE+BE=BC+AD=7.答案:7
7.如图,AB=CD,BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.【证明】在Rt△ABF和Rt△CDE中,∵AE=CF,∴AF=CE,又∵AB=CD,∴△ABF≌△CDE,∴BF=DE.
8.在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF.(2)若∠CAE=30°,求∠ACF的度数.
【解析】(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°,在Rt△ABE和Rt△CBF中,∴Rt△ABE≌Rt△CBF(HL).
(2)∵AB=BC,∠ABC=90°,∴∠CAB=∠ACB=45°,又∵∠BAE=∠CAB-∠CAE=45°-30°=15°,由(1)知:Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=15°,∴∠ACF=∠BCF+∠ACB=15°+45°=60°.
【想一想错在哪？】已知,如图,在△ABC中,AD是它的角平分线,　　　　　且AB=AC,DE,DF分别与AB,AC垂直,垂足为E,F,求证:BE=CF.提示:在使用“HL”判定△ABD≌△ACD时,要先说明这两个三角形是直角三角形.