初中数学北师大版八年级下册3 公式法精品课件ppt

这是一份初中数学北师大版八年级下册3 公式法精品课件ppt，共25页。PPT课件主要包含了因式分解，整式乘法，完全平方公式，必须是三项式，练习题等内容，欢迎下载使用。
课前小测：1.选择题：1)下列各式能用平方差公式分解因式的是（ ）4X²+y² B. 4 x- (-y)² C. -4 X²-y³ D. - X²+ y²-4a² +1分解因式的结果应是 （ ）-(4a+1)(4a-1) B. -( 2a –1)(2a –1)-(2a +1)(2a+1) D. -(2a+1) (2a-1)2. 把下列各式分解因式：1）18-2b² 2) x4 –1
因式分解的基本方法2
运用公式法 把乘法公式反过来用,可以把符合公式特点的多项式因式分解,这种方法叫公式法.
　 (1) 平方差公式： a2-b2=(a+b)(a-b) (2) 完全平方公式：a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
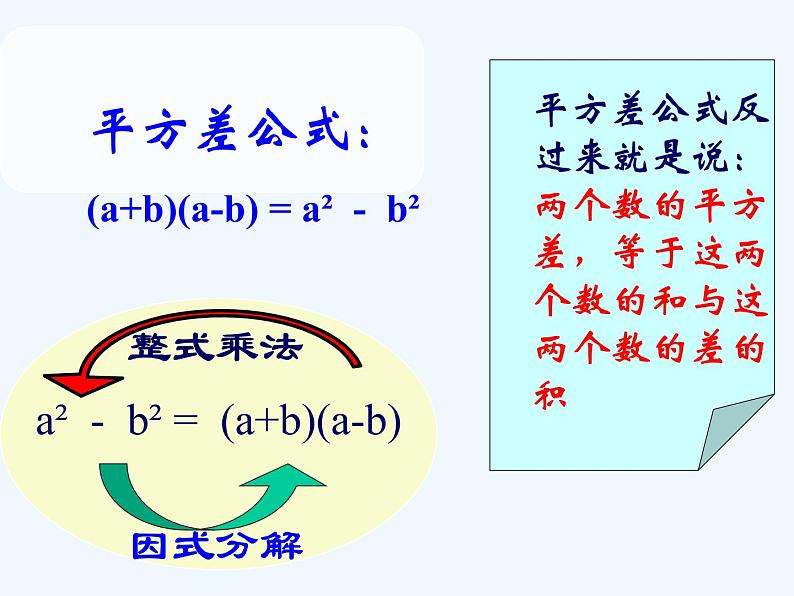
平方差公式反过来就是说：两个数的平方差，等于这两个数的和与这两个数的差的积
a² - b² = (a+b)(a-b)
平方差公式：(a+b)(a-b) = a² - b²
将下面的多项式分解因式1) m² - 16 2) 4x² - 9y²
m² - 16= m² - 4² =( m + 4)( m - 4)
a² - b² = ( a + b)( a - b )
4x² - 9y²=(2x)²-(3y)²=(2x+3y)(2x-3y)
例1.把下列各式分解因式（1）16a²- 1 ( 2 ) 4x²- m²n² ( 3 ) — x² - — y²
( 4 ) –9x² + 4
解：1）16a²-1=(4a)² - 1 =(4a+1)(4a-1)
解：2） 4x²- m²n² =(2x)² - (mn)² =（2x+mn)(2x-mn)
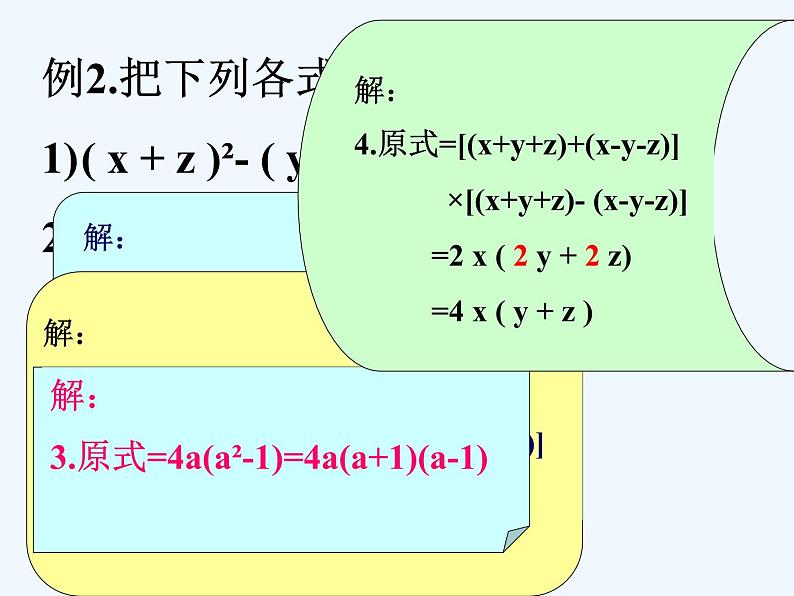
例2.把下列各式因式分解( x + z )²- ( y + z )²4( a + b)² - 25(a - c)²4a³ - 4a(x + y + z)² - (x – y – z )²5)—a² - 2
巩固练习：1.选择题：1)下列各式能用平方差公式分解因式的是（ ）4X²+y² B. 4 x- (-y)² C. -4 X²-y³ D. - X²+ y²-4a² +1分解因式的结果应是 （ ）-(4a+1)(4a-1) B. -( 2a –1)(2a –1)-(2a +1)(2a+1) D. -(2a+1) (2a-1)2. 把下列各式分解因式：1）18-2b² 2) x4 –1
现在我们把这个公式反过来
很显然，我们可以运用以上这个公式来分解因式了，我们把它称为“完全平方公式”
我们把以上两个式子叫做完全平方式
“头” 平方, “尾” 平方, “头” “尾”两倍中间放.
判别下列各式是不是完全平方式
2、有两个平方的“项”
3、有这两平方“项”底数的2倍或-2倍
下列各式是不是完全平方式
请补上一项，使下列多项式成为完全平方式
我们可以通过以上公式把“完全平方式”分解因式我们称之为：运用完全平方公式分解因式
例题：把下列式子分解因式
4x2+12xy+9y2
请运用完全平方公式把下列各式分解因式：
1、下列各式中，能用完全平方公式分解的是（ ）A、a2+b2+ab B、a2+2ab-b2 C、a2-ab+2b2 D、-2ab+a2+b22、下列各式中，不能用完全平方公式分解的是（ ）A、x2+y2-2xy B、x2+4xy+4y2 C、a2-ab+b2 D、-2ab+a2+b2
3、下列各式中，能用完全平方公式分解的是（ ）A、x2+2xy-y2 B、x2-xy+y2 C、 D、4、下列各式中，不能用完全平方公式分解的是（ ）A、x4+6x2y2+9y4 B、x2n-2xnyn+y2n C、x6-4x3y3+4y6 D、x4+x2y2+y4
7、如果100x2+kxy+y2可以分解为（10x-y)2,那么k的值是（ ）A、20 B、-20 C、10 D、-108、如果x2+mxy+9y2是一个完全平方式，那么m的值为（ ）A、6 B、±6 C、3 D、±3
9、把 分解因式得（ ）A、 B、C、 D、10、计算 的结果是（ ）A、 1 B、-1C、 2 D、-2
思考题:1、多项式:(x+y)2-2(x2-y2)+(x-y)2能用完全平方公式分解吗?2、在括号内补上一项，使多项式成为完全平方式：X4+4x2+( )