

还剩10页未读,
继续阅读
广东省深圳市龙华2019-2020学年七年级(下)期末数学复习试卷 附答案
展开
广东省深圳市龙华2019-2020学年七年级(下)期末数学复习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.代数式(2a2)3的计算结果是( )
A.2a6 B.6a5 C.8a5 D.8a6
2.下列图形中,是轴对称图形的是( )
A. B.
C. D.
3.下列式子中,一定是二次根式的是( )
A. B. C. D.
4.如图所示,AB是一条直线,若∠1=∠2,则∠3=∠4,其理由是( )
A.内错角相等 B.等角的补角相等
C.同角的补角相等 D.等量代换
5.下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
6.设三角形三边之长分别为3,8,2a,则a的取值范围为( )
A.1.5<a<4.5 B.2.5<a<5.5 C.3.5<a<6.5 D.4.5<a<7.5
7.将一根长为10cm的铁丝制作成一个长方形,则这个长方形的长y(cm)与宽x(cm)之间的关系式为( )
A.y=﹣x+5 B.y=x+5 C.y=﹣x+10 D.y=x+10
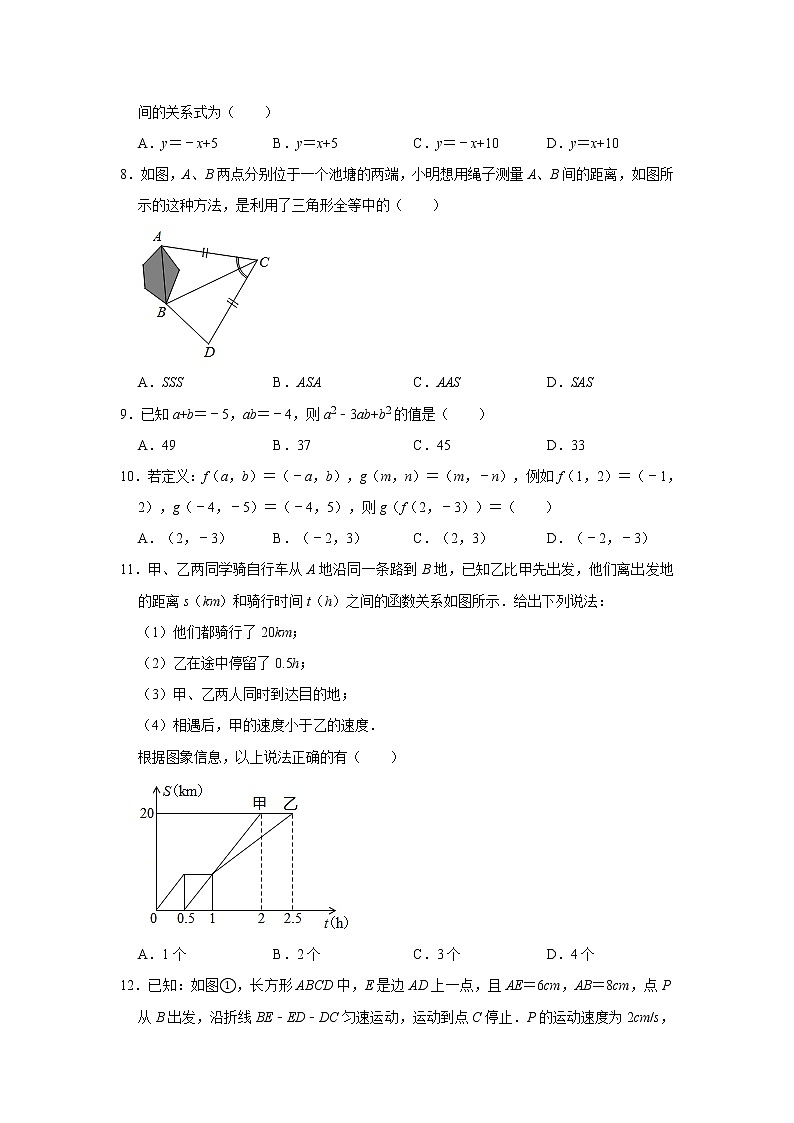
8.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
9.已知a+b=﹣5,ab=﹣4,则a2﹣3ab+b2的值是( )
A.49 B.37 C.45 D.33
10.若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f(1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(2,﹣3))=( )
A.(2,﹣3) B.(﹣2,3) C.(2,3) D.(﹣2,﹣3)
11.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示.给出下列说法:
(1)他们都骑行了20km;
(2)乙在途中停留了0.5h;
(3)甲、乙两人同时到达目的地;
(4)相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )
A.1个 B.2个 C.3个 D.4个
12.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,AB=8cm,点P从B出发,沿折线BE﹣ED﹣DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )
①a=7 ②b=10③当t=3s时△PCD为等腰三角形 ④当t=10s时,y=12cm2
A.1个 B.2个 C.3个 D.4个
二.填空题(共4小题,满分12分,每小题3分)
13.等腰三角形有一外角为100°,则它的底角为 .
14.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是 .(只需添加一个条件即可)
15.如图,在△ABC中,AD是边BC上的高,BE平分∠ABC交AC于点E,∠BAC=60°,∠EBC=25°,则∠DAC= °.
16.已知长方形ABCD,E点和F点分别在AB和BC边上,如图将△BEF沿着EF折叠以后得到△B′EF,B′E与AD相交于点M,B′F与AD相交于点G,则∠1与∠2的数量关系为 .
三.解答题(本大题有7题,其中17题12分,18题6分,19题6分,20题6分,21题7分,22题7分,23题8分,共52分)
17.计算:
(1)(﹣)﹣2+(2018﹣π)0﹣|﹣4|
(2)[a(a2b2﹣ab)﹣b(﹣a3b﹣a2)]÷a2b
18.先化简,再求值:(a+3)2﹣(a+1)(a﹣1)﹣2(2a+4),其中a=.
19.如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
求:
(1)转动转盘,转出的数字大于3的概率是多少;
(2)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?
20.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)在这个变化过程中, 是自变量, 是因变量;
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
21.如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
(1)求证:△AEC≌△BED.
(2)若∠1=40°,求∠BDE的度数.
22.阅读:若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值.
解:设(80﹣x)=a,(x﹣60)=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20
所以(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340
请仿照上例解决下面的问题:
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值.
(2)若x满足(2019﹣x)2+(2018﹣x)2=2017,求(2019﹣x)(2018﹣x)的值.
(3)如图,正方形ABCD的边长为x,AE=10,CG=25,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体数值).
23.如图,已知正方形ABCD(四边相等,四个角都是直角),点E为边AB上异于点A、B的一动点,EF∥AC,交BC于点F,点G为DA延长线上一定点,满足AG=AD,GE的延长线与DF交于点H,连接BH.
(1)判断△BEF是 三角形.
(2)求证:△AGE≌△CDF.
(3)探究∠EHB是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:原式=23•(a2)3=8a6,
故选:D.
2.解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:B.
3.解:A、当x<﹣1即x+1<0时,它不是二次根式,故本选项不符合题意.
B、由于﹣5<0,则它无意义,故本选项不符合题意.
C、由于x2+1>0,所以它符合二次根式的定义,故本选项符合题意.
D、当x2﹣1<0时,它无意义,故本选项不符合题意.
故选:C.
4.解:∵∠1=∠2,
∴∠3=∠4(等角的补角相等).
故选:B.
5.解:“对顶角相等”是真命题,发生的可能性为100%,
故选:D.
6.解:由题意,得
8﹣3<2a<8+3,
即5<2a<11,
解得:2.5<a<5.5.
故选:B.
7.解:由题意得:这个长方形的长y(cm)与宽x(cm)之间的关系式为:y=﹣x+5,
故选:A.
8.解:观察图形发现:AC=DC,BC=BC,∠ACB=∠DCB,
所以利用了三角形全等中的SAS,
故选:D.
9.解:∵a+b=﹣5,ab=﹣4,
∴a2﹣3ab+b2=(a+b)2﹣5ab=52﹣5×(﹣4)=25+20=45,
故选:C.
10.解:根据定义,f(2,﹣3)=(﹣2,﹣3),
所以,g(f(2,﹣3))=g(﹣2,﹣3)=(﹣2,3).
故选:B.
11.解:由图可获取的信息是:他们都骑行了20km;乙在途中停留了0.5h;相遇后,甲的速度>乙的速度,所以甲比乙早0.5小时到达目的地,所以(1)(2)正确.
故选:B.
12.解:当P点运动到E点时,△BPC面积最大,结合函数图象可知当t=5时,△BPC面积最大为40,
∴BE=5×2=10.
∵•BC•AB=40,
∴BC=10.
则ED=10﹣6=4.当P点从E点到D点时,所用时间为4÷2=2s,
∴a=5+2=7.
故①正确;
P点运动完整个过程需要时间t=(10+4+8)÷2=11s,即b=11,②错误;
当t=3时,BP=AE=6,
∵S△BPC=S△EAB=24,
∴CP=AB=8,
∴CP=CD=8,
∴△PCD是等腰三角形,故③正确;
当t=10时,P点运动的路程为10×2=20cm,此时PC=22﹣20=2,
△BPC面积为×10×2=10cm2,④错误.
∴正确的结论有①③.
故选:B.
二.填空题(共4小题,满分12分,每小题3分)
13.解:∵等腰三角形的一个外角等于100°,
∴等腰三角形的一个内角为80°,
①当80°为顶角时,其他两角都为50°、50°,
②当80°为底角时,其他两角为80°、20°,
所以等腰三角形的底角可以是50°,也可以是80°
答案为:80°或50°.
14.解:当∠D=∠B时,
在△ADF和△CBE中
∵,
∴△ADF≌△CBE(SAS),
故答案为:∠D=∠B.(答案不唯一)
15.解:∵BE平分∠ABC,∠EBC=25°,
∴∠ABC=2∠EBC=50°,
∵∠BAC+∠ABC+∠C=180°,∠BAC=60°,
∴∠C=180°﹣60°﹣50°=70°,
又∵AD是边BC上的高,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=90°﹣70°=20°,
故答案为:20
16.解:由折叠可得,∠B=∠B'=90°,∠BEB'=2∠2,
∴∠BFE+∠BEB'=180°,
∵AD∥BC,
∴∠1=∠GFC,
又∵∠BFE+∠GFC=180°,
∴∠BFE+∠1=180°,
∴∠BEB'=∠1,
即2∠2=∠1,
故答案为:∠1=2∠2.
三.解答题(本大题有7题,其中17题12分,18题6分,19题6分,20题6分,21题7分,22题7分,23题8分,共52分
17.解:(1))(﹣)﹣2+(2018﹣π)0﹣|﹣4|
=4+1﹣4
=1;
(2)[a(a2b2﹣ab)﹣b(﹣a3b﹣a2)]÷a2b
=(a3b2﹣a2b+a3b2+a2b)÷a2b
=2a3b2÷a2b
=2ab.
18.解:原式=a2+6a+9﹣(a2﹣1)﹣4a﹣8
=2a+2,
∵a=,
∴原式=1+2=3.
19.解:(1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
∴转出的数字大于3的概率是=;
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,
∴这三条线段能构成三角形的概率是;
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,
∴这三条线段能构成等腰三角形的概率是=.
20.解:(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元;
(4)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月利润为5000元时,每月乘车人数为4500人,
故答案为4500.
21.(1)证明:∵∠1=∠2,
∴∠1+∠AED=∠2+∠AED,
∴∠AEC=∠BED,
在△AEC和△BED中
∴△AEC≌△BED(ASA);
(2)∵△AEC≌△BED,
∴ED=EC,∠ACE=∠BDE,
∴∠ECD=∠EDC,
∵∠1=40°,
∴∠ECD=∠EDC=70°,
∴∠ECA=70°,
∴∠BDE=70°,
即∠BDE是70°.
22.解:(1)设30﹣x=a,x﹣20=b,作为ab=﹣10,a+b=10,
原式=a2+b2=(a+b)2﹣2ab=102﹣2×(﹣10)=120.
(2)设2019﹣x=m,2018﹣x=n,则m2+n2=2017,m﹣n=1,
∵(m﹣n)2=m2﹣2mn+n2,
∴1=2017﹣2mn,
∴mn=1008,即(2019﹣x)(2018﹣x)=1008.
(3)由题意DE=x﹣10,DG=x﹣25,则(x﹣10)(x﹣25)=500,
设a=x﹣10,b=x﹣25,则a﹣b=15,ab=500,
∴S阴=(a+b)2=(a﹣b)2+4ab=152+4×500=2225.
23.解:(1)△BEF是等腰直角三角形,
∵正方形ABCD中,AB=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∵AC∥EF,
∴△BEF是等腰直角三角形;
故答案为:等腰直角;
(2)证明:如图1,
∵△ABC和△BEF为等腰直角三角形,
∴AB=BC,BE=BF,
∴AB﹣BE=BC﹣BF,即是AE=FC,
∵四边形ABCD为正方形,
∴AD=CD=AG,∠GAE=∠DCF=90°,
∴△AGE≌△CDF(SAS),
(3)∠EHB=45°.
如图2,在GE上截取ME=HF,
∵△AGE≌△CDF,
∴∠AEG=∠DFC
∴180﹣∠AEG=180﹣∠DFC
即是∠MEB=∠HFB,
∵△BEF为等腰直角三角形,
∴BE=BF,
∵BE=BF,ME=HF,∠MEB=∠HFB,
∴△MEB≌△HFB(SAS),
∴∠MBE=∠HBF,MB=BH,
∵∠HBF+∠EBH=90°,
∴∠MBE+∠EBH=90°即是∠MBH=90°
∴△MBH为等腰直角三角形,
∴∠EHB=45°.
广东省深圳市龙华2019-2020学年七年级(下)期末数学复习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.代数式(2a2)3的计算结果是( )
A.2a6 B.6a5 C.8a5 D.8a6
2.下列图形中,是轴对称图形的是( )
A. B.
C. D.
3.下列式子中,一定是二次根式的是( )
A. B. C. D.
4.如图所示,AB是一条直线,若∠1=∠2,则∠3=∠4,其理由是( )
A.内错角相等 B.等角的补角相等
C.同角的补角相等 D.等量代换
5.下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
6.设三角形三边之长分别为3,8,2a,则a的取值范围为( )
A.1.5<a<4.5 B.2.5<a<5.5 C.3.5<a<6.5 D.4.5<a<7.5
7.将一根长为10cm的铁丝制作成一个长方形,则这个长方形的长y(cm)与宽x(cm)之间的关系式为( )
A.y=﹣x+5 B.y=x+5 C.y=﹣x+10 D.y=x+10
8.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
9.已知a+b=﹣5,ab=﹣4,则a2﹣3ab+b2的值是( )
A.49 B.37 C.45 D.33
10.若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f(1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(2,﹣3))=( )
A.(2,﹣3) B.(﹣2,3) C.(2,3) D.(﹣2,﹣3)
11.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示.给出下列说法:
(1)他们都骑行了20km;
(2)乙在途中停留了0.5h;
(3)甲、乙两人同时到达目的地;
(4)相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )
A.1个 B.2个 C.3个 D.4个
12.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,AB=8cm,点P从B出发,沿折线BE﹣ED﹣DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )
①a=7 ②b=10③当t=3s时△PCD为等腰三角形 ④当t=10s时,y=12cm2
A.1个 B.2个 C.3个 D.4个
二.填空题(共4小题,满分12分,每小题3分)
13.等腰三角形有一外角为100°,则它的底角为 .
14.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是 .(只需添加一个条件即可)
15.如图,在△ABC中,AD是边BC上的高,BE平分∠ABC交AC于点E,∠BAC=60°,∠EBC=25°,则∠DAC= °.
16.已知长方形ABCD,E点和F点分别在AB和BC边上,如图将△BEF沿着EF折叠以后得到△B′EF,B′E与AD相交于点M,B′F与AD相交于点G,则∠1与∠2的数量关系为 .
三.解答题(本大题有7题,其中17题12分,18题6分,19题6分,20题6分,21题7分,22题7分,23题8分,共52分)
17.计算:
(1)(﹣)﹣2+(2018﹣π)0﹣|﹣4|
(2)[a(a2b2﹣ab)﹣b(﹣a3b﹣a2)]÷a2b
18.先化简,再求值:(a+3)2﹣(a+1)(a﹣1)﹣2(2a+4),其中a=.
19.如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
求:
(1)转动转盘,转出的数字大于3的概率是多少;
(2)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?
20.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)在这个变化过程中, 是自变量, 是因变量;
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
21.如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
(1)求证:△AEC≌△BED.
(2)若∠1=40°,求∠BDE的度数.
22.阅读:若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值.
解:设(80﹣x)=a,(x﹣60)=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20
所以(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340
请仿照上例解决下面的问题:
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值.
(2)若x满足(2019﹣x)2+(2018﹣x)2=2017,求(2019﹣x)(2018﹣x)的值.
(3)如图,正方形ABCD的边长为x,AE=10,CG=25,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体数值).
23.如图,已知正方形ABCD(四边相等,四个角都是直角),点E为边AB上异于点A、B的一动点,EF∥AC,交BC于点F,点G为DA延长线上一定点,满足AG=AD,GE的延长线与DF交于点H,连接BH.
(1)判断△BEF是 三角形.
(2)求证:△AGE≌△CDF.
(3)探究∠EHB是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:原式=23•(a2)3=8a6,
故选:D.
2.解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:B.
3.解:A、当x<﹣1即x+1<0时,它不是二次根式,故本选项不符合题意.
B、由于﹣5<0,则它无意义,故本选项不符合题意.
C、由于x2+1>0,所以它符合二次根式的定义,故本选项符合题意.
D、当x2﹣1<0时,它无意义,故本选项不符合题意.
故选:C.
4.解:∵∠1=∠2,
∴∠3=∠4(等角的补角相等).
故选:B.
5.解:“对顶角相等”是真命题,发生的可能性为100%,
故选:D.
6.解:由题意,得
8﹣3<2a<8+3,
即5<2a<11,
解得:2.5<a<5.5.
故选:B.
7.解:由题意得:这个长方形的长y(cm)与宽x(cm)之间的关系式为:y=﹣x+5,
故选:A.
8.解:观察图形发现:AC=DC,BC=BC,∠ACB=∠DCB,
所以利用了三角形全等中的SAS,
故选:D.
9.解:∵a+b=﹣5,ab=﹣4,
∴a2﹣3ab+b2=(a+b)2﹣5ab=52﹣5×(﹣4)=25+20=45,
故选:C.
10.解:根据定义,f(2,﹣3)=(﹣2,﹣3),
所以,g(f(2,﹣3))=g(﹣2,﹣3)=(﹣2,3).
故选:B.
11.解:由图可获取的信息是:他们都骑行了20km;乙在途中停留了0.5h;相遇后,甲的速度>乙的速度,所以甲比乙早0.5小时到达目的地,所以(1)(2)正确.
故选:B.
12.解:当P点运动到E点时,△BPC面积最大,结合函数图象可知当t=5时,△BPC面积最大为40,
∴BE=5×2=10.
∵•BC•AB=40,
∴BC=10.
则ED=10﹣6=4.当P点从E点到D点时,所用时间为4÷2=2s,
∴a=5+2=7.
故①正确;
P点运动完整个过程需要时间t=(10+4+8)÷2=11s,即b=11,②错误;
当t=3时,BP=AE=6,
∵S△BPC=S△EAB=24,
∴CP=AB=8,
∴CP=CD=8,
∴△PCD是等腰三角形,故③正确;
当t=10时,P点运动的路程为10×2=20cm,此时PC=22﹣20=2,
△BPC面积为×10×2=10cm2,④错误.
∴正确的结论有①③.
故选:B.
二.填空题(共4小题,满分12分,每小题3分)
13.解:∵等腰三角形的一个外角等于100°,
∴等腰三角形的一个内角为80°,
①当80°为顶角时,其他两角都为50°、50°,
②当80°为底角时,其他两角为80°、20°,
所以等腰三角形的底角可以是50°,也可以是80°
答案为:80°或50°.
14.解:当∠D=∠B时,
在△ADF和△CBE中
∵,
∴△ADF≌△CBE(SAS),
故答案为:∠D=∠B.(答案不唯一)
15.解:∵BE平分∠ABC,∠EBC=25°,
∴∠ABC=2∠EBC=50°,
∵∠BAC+∠ABC+∠C=180°,∠BAC=60°,
∴∠C=180°﹣60°﹣50°=70°,
又∵AD是边BC上的高,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=90°﹣70°=20°,
故答案为:20
16.解:由折叠可得,∠B=∠B'=90°,∠BEB'=2∠2,
∴∠BFE+∠BEB'=180°,
∵AD∥BC,
∴∠1=∠GFC,
又∵∠BFE+∠GFC=180°,
∴∠BFE+∠1=180°,
∴∠BEB'=∠1,
即2∠2=∠1,
故答案为:∠1=2∠2.
三.解答题(本大题有7题,其中17题12分,18题6分,19题6分,20题6分,21题7分,22题7分,23题8分,共52分
17.解:(1))(﹣)﹣2+(2018﹣π)0﹣|﹣4|
=4+1﹣4
=1;
(2)[a(a2b2﹣ab)﹣b(﹣a3b﹣a2)]÷a2b
=(a3b2﹣a2b+a3b2+a2b)÷a2b
=2a3b2÷a2b
=2ab.
18.解:原式=a2+6a+9﹣(a2﹣1)﹣4a﹣8
=2a+2,
∵a=,
∴原式=1+2=3.
19.解:(1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
∴转出的数字大于3的概率是=;
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,
∴这三条线段能构成三角形的概率是;
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,
∴这三条线段能构成等腰三角形的概率是=.
20.解:(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元;
(4)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月利润为5000元时,每月乘车人数为4500人,
故答案为4500.
21.(1)证明:∵∠1=∠2,
∴∠1+∠AED=∠2+∠AED,
∴∠AEC=∠BED,
在△AEC和△BED中
∴△AEC≌△BED(ASA);
(2)∵△AEC≌△BED,
∴ED=EC,∠ACE=∠BDE,
∴∠ECD=∠EDC,
∵∠1=40°,
∴∠ECD=∠EDC=70°,
∴∠ECA=70°,
∴∠BDE=70°,
即∠BDE是70°.
22.解:(1)设30﹣x=a,x﹣20=b,作为ab=﹣10,a+b=10,
原式=a2+b2=(a+b)2﹣2ab=102﹣2×(﹣10)=120.
(2)设2019﹣x=m,2018﹣x=n,则m2+n2=2017,m﹣n=1,
∵(m﹣n)2=m2﹣2mn+n2,
∴1=2017﹣2mn,
∴mn=1008,即(2019﹣x)(2018﹣x)=1008.
(3)由题意DE=x﹣10,DG=x﹣25,则(x﹣10)(x﹣25)=500,
设a=x﹣10,b=x﹣25,则a﹣b=15,ab=500,
∴S阴=(a+b)2=(a﹣b)2+4ab=152+4×500=2225.
23.解:(1)△BEF是等腰直角三角形,
∵正方形ABCD中,AB=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∵AC∥EF,
∴△BEF是等腰直角三角形;
故答案为:等腰直角;
(2)证明:如图1,
∵△ABC和△BEF为等腰直角三角形,
∴AB=BC,BE=BF,
∴AB﹣BE=BC﹣BF,即是AE=FC,
∵四边形ABCD为正方形,
∴AD=CD=AG,∠GAE=∠DCF=90°,
∴△AGE≌△CDF(SAS),
(3)∠EHB=45°.
如图2,在GE上截取ME=HF,
∵△AGE≌△CDF,
∴∠AEG=∠DFC
∴180﹣∠AEG=180﹣∠DFC
即是∠MEB=∠HFB,
∵△BEF为等腰直角三角形,
∴BE=BF,
∵BE=BF,ME=HF,∠MEB=∠HFB,
∴△MEB≌△HFB(SAS),
∴∠MBE=∠HBF,MB=BH,
∵∠HBF+∠EBH=90°,
∴∠MBE+∠EBH=90°即是∠MBH=90°
∴△MBH为等腰直角三角形,
∴∠EHB=45°.
相关资料
更多








