

2020届辽宁省丹东市高三第一次模拟考试理科数学试题
展开2020年丹东市高三总复习质量测试(一)
理科数学
本试卷共23题,共150分,共4页。考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|-1<x<1},B={x|0<x<2},则A∪B=
A.(-1,2) | B.(0,1) | C.(-1,0) | D.(1,2) |
2.已知向量a=(1,2),b=(-2,3),c=(1,1),若(a+λb)⊥c,则实数λ=
A.- | B. | C.-3 | D.3 |
3.设a∈R,若(a+i)(1-ai)>0,则a=
A.-1 | B.1 | C.0 | D.±1 |
4.中国古代数学著作《九章算术》有如下问题:“今有女子善织,日增等尺,七日织二十八尺,第二日、第五日、第八日所织之和为一十五尺”,则该女子第六日所织
A.5尺 | B.6尺 | C.7尺 | D.8尺 |
5.右图是相关变量x,y的散点图,现对这两个变量进行线性相关分析,分析一:由图中所有数据,得到线性回归方程y=b1x+a1,相关系数为r1.分析二:剔除点P,由剩下数据得到线性回归直线方程y=b2x+a2,相关系数为r2.那么
A.0<r1<r2<1 |
B.0<r2<r1<1 |
C.-1<r1<r2<0 |
D.-1<r2<r1<0 |
6.已知双曲线C:-=1(a>0,b>0)的一条渐近线与圆(x-a)2+y2=相切,则C的离心率为
A. | B. | C.2 | D. |
7.已知实数a,b,c分别满足2a=-a,log0.5b=b,log2c=,那么
A.a<b<c | B.a<c<b | C.b<c<a | D.c<b<a |
8.已知m,n是两条异面直线,直线l与m,n都垂直,则下列说法正确的是
A.若l⊂平面α,则m⊥α |
B.若l⊥平面α,则m∥α,n∥α |
C.存在平面α,使得l⊥α,m⊂α,n∥α |
D.存在平面α,使得l∥α,m⊥α,n⊥α |
9.已知函数f (x)=,那么
A.f (x)有极小值,也有大极值 | B.f (x)有极小值,没有极大值 |
C.f (x)有极大值,没有极小值 | D.f (x)没有极值 |
10.已知ω>0,在函数f (x)=sinωx和函数g (x)=cosωx的图象的交点中,距离最短的两个交点的距离为2,下述四个结论:
①ω= ②f (x)在[0,2π]有3个零点
③任意连续三个交点组成的三角形面积为8
④为了得到y=g (x)的图象,只需把y=f (x)的图象向左平移1个单位
其中所有正确结论的编号是
A.①② | B.②③ | C.①③ | D.①④ |
11.已知抛物线C:y2=8x的焦点为F,准线为l,点M在C上,点N在l上,直线MN经过点P(0,4),若MF⊥NF,则|MF|=
A.8 | B.10 | C.12 | D.16 |
12.已知函数f (x)=1-x+ln,则满足f (x-1)+f (x)<2的x的取值范围是
A.(-1,0) | B.(0,1) | C.(-1,) | D.(,1) |
二、填空题:本题共4小题,每小题5分,共20分。
13.(1+x2)(1+x)4展开式中含x5项的系数为________.
14.曲线y=ln(1+x)在x=0处的切线方程为y=f (x),则f (x)=_______.因此当|x|很小时,ln(1+x)≈f (x),由于ln2≈0.6931,于是≈=.某金融业的一种长期理财品种采用复利方式计算利息,年利率为3.3%,按照上面的近似等式,
本息和不小于本金的2倍,至少需经过________年.
(本题第一空2分,第二空3分)
15.已知Sn为数列{an}的前n项和,若S2=3,an+1=Sn+1,则Sn=________.
16.四面体ABCD中,AB⊥AC,AC⊥CD,AB与CD所成角为30º,AB=5,AC=4,
CD=3,则四面体ABCD的体积为________.
三、解答题:共70分。解答应写出文字说明,证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
如图,直四棱柱ABCD-A1B1C1D1中,侧棱
AA1⊥底面ABCD,底面ABCD是平行四边形,
AB=1,AC=,BC=2.
(1)求证:AC⊥平面AA1B1B;
(2)若BB1=BC,求二面角A-C1D-C的余弦值.
18.(12分)
已知△ABC同时满足下列四个条件中的三个条件:
①A=; ②cosB=-; ③a=7; ④b=3.
其中a,b,c分别是△ABC内角A,B,C的对边.
(1)请指出这三个条件,并说明理由;
(2)求cos(C-)的值.
19.(12分)
某省高考实行新方案,将采用“3+1+2”模式,其中“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在物理、历史科目中选择一科;“2”为再选科目,考生可在化学、生物、地理、思想政治4个科目中选择两科.
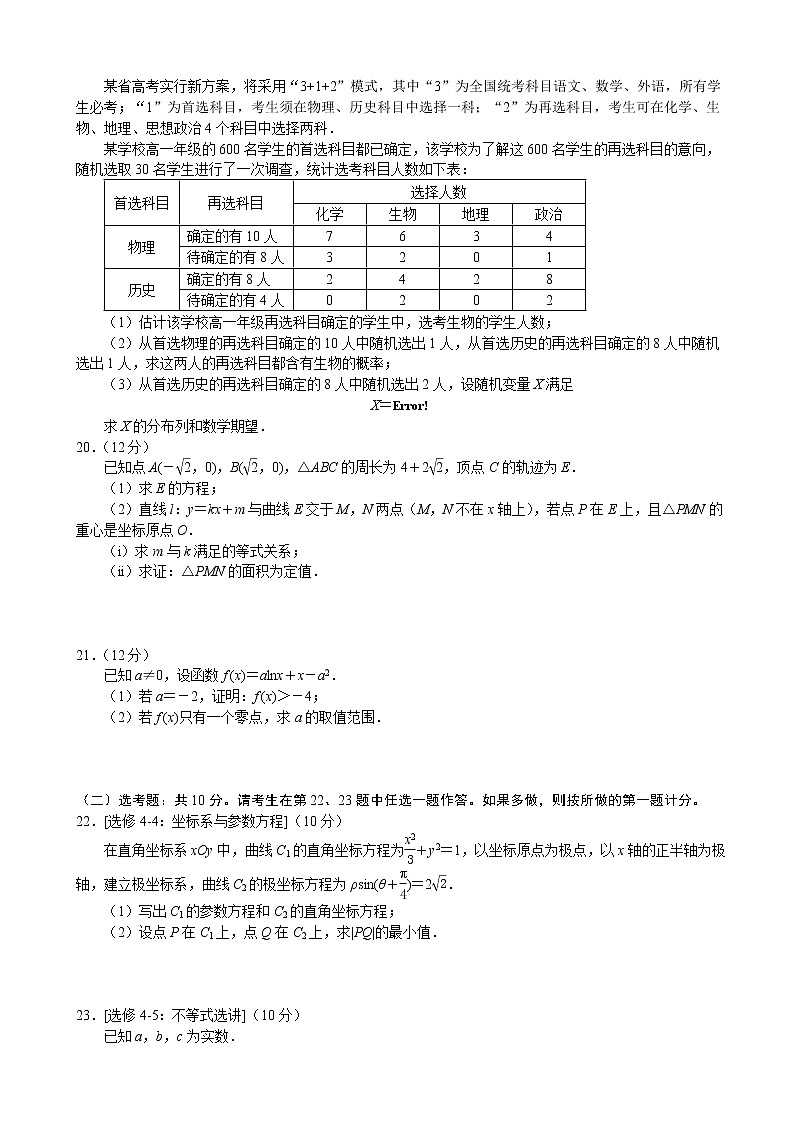
某学校高一年级的600名学生的首选科目都已确定,该学校为了解这600名学生的再选科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
首选科目 | 再选科目 | 选择人数 | |||
化学 | 生物 | 地理 | 政治 | ||
物理 | 确定的有10人 | 7 | 6 | 3 | 4 |
待确定的有8人 | 3 | 2 | 0 | 1 | |
历史 | 确定的有8人 | 2 | 4 | 2 | 8 |
待确定的有4人 | 0 | 2 | 0 | 2 | |
(1)估计该学校高一年级再选科目确定的学生中,选考生物的学生人数;
(2)从首选物理的再选科目确定的10人中随机选出1人,从首选历史的再选科目确定的8人中随机选出1人,求这两人的再选科目都含有生物的概率;
(3)从首选历史的再选科目确定的8人中随机选出2人,设随机变量X满足
X=
求X的分布列和数学期望.
20.(12分)
已知点A(-,0),B(,0),△ABC的周长为4+2,顶点C的轨迹为E.
(1)求E的方程;
(2)直线l:y=kx+m与曲线E交于M,N两点(M,N不在x轴上),若点P在E上,且△PMN的重心是坐标原点O.
(i)求m与k满足的等式关系;
(ii)求证:△PMN的面积为定值.
21.(12分)
已知a≠0,设函数f (x)=alnx+x-a2.
(1)若a=-2,证明:f (x)>-4;
(2)若f (x)只有一个零点,求a的取值范围.
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xOy中,曲线C1的直角坐标方程为+y2=1,以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+)=2.
(1)写出C1的参数方程和C2的直角坐标方程;
(2)设点P在C1上,点Q在C2上,求|PQ|的最小值.
23.[选修4-5:不等式选讲](10分)
已知a,b,c为实数.
(1)证明:a2+b2+c2≥ab+bc+ca;
(2)若a+b+c=1,求(a-1)2+(b-2)2+(c-3)2的最小值.








