2020年吉林省长春市中考数学考前适应性练习试卷 解析版

2020年吉林省长春市中考数学考前适应性练习试卷
一．选择题（共8小题，满分24分，每小题3分）
1．|﹣3|等于（　　）
A．﹣3 B．﹣ C．3 D．
2．在国家大数据战略的引领下，我国在人工智能领域取得显著成就，自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军，这得益于所建立的大数据中心的规模和数据存储量，它们决定着人工智能深度学习的质量和速度，其中的一个大数据中心能存储58000000000本书籍，将58000000000用科学记数法表示应为（　　）
A．5.8×1010 B．5.8×1011 C．58×109 D．0.58×1011
3．下列几何体中，俯视图为三角形的是（　　）
A． B． C． D．
4．不等式x﹣1＞0 的解在数轴上表示为（　　）
A． B．
C． D．
5．如图，在△ABC中，点D在AB边上，点E在AC边上DE∥BC，点B、C、F在一条直线上，若∠ACF＝140°，∠ADE＝105°，则∠A的大小为（　　）

A．75° B．50° C．35° D．30°
6．如图，放映幻灯片时，通过光源把幻灯片上的图形放大到屏幕上，若光源到幻灯片的距离为20cm，到屏幕的距离为60cm，且幻灯片中的图形的高度为6cm，则屏幕上图形的高度为（　　）

A．6cm B．12cm C．18cm D．24cm
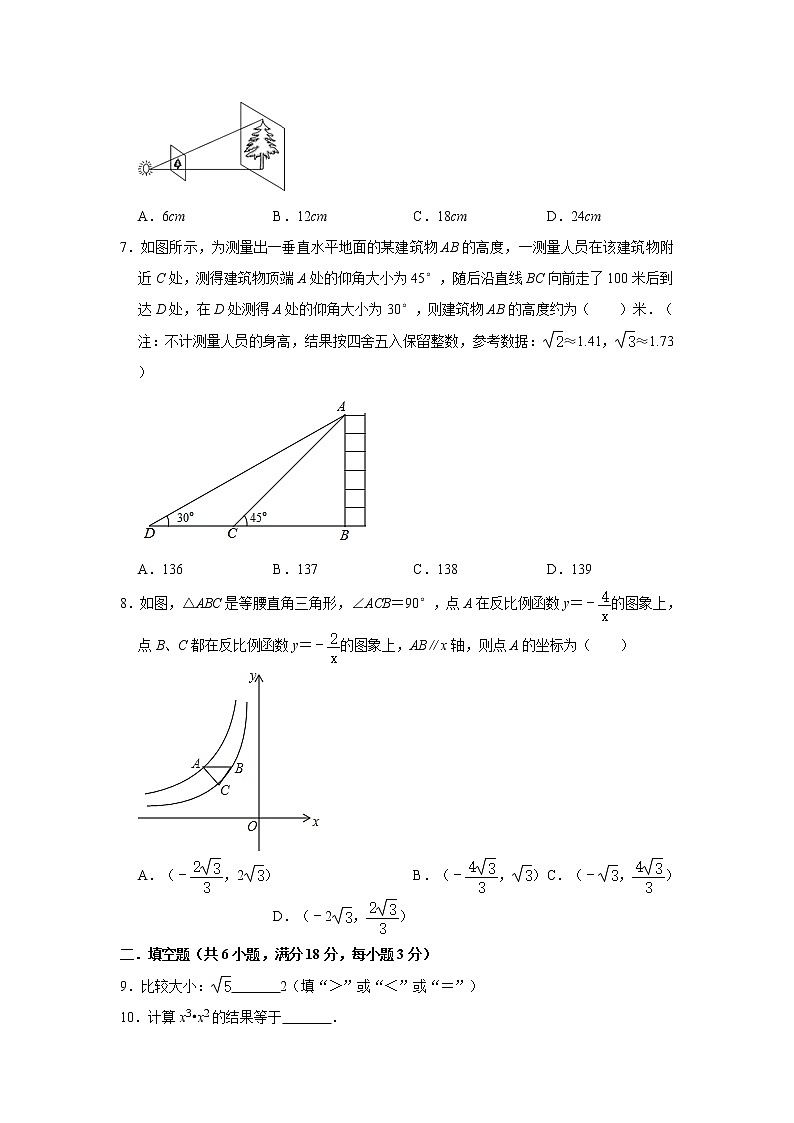
7．如图所示，为测量出一垂直水平地面的某建筑物AB的高度，一测量人员在该建筑物附近C处，测得建筑物顶端A处的仰角大小为45°，随后沿直线BC向前走了100米后到达D处，在D处测得A处的仰角大小为30°，则建筑物AB的高度约为（　　）米．（注：不计测量人员的身高，结果按四舍五入保留整数，参考数据：≈1.41，≈1.73）

A．136 B．137 C．138 D．139
8．如图，△ABC是等腰直角三角形，∠ACB＝90°，点A在反比例函数y＝﹣的图象上，点B、C都在反比例函数y＝﹣的图象上，AB∥x轴，则点A的坐标为（　　）

A．（﹣，2） B．（﹣，） C．（﹣，） D．（﹣2，）
二．填空题（共6小题，满分18分，每小题3分）
9．比较大小：　 　2（填“＞”或“＜”或“＝”）
10．计算x3•x2的结果等于　 　．
11．如图，在平面直角坐标系中，点A、B的坐标分别为（1，4）、（n，4），若直线y＝2x与线段AB有公共点，则n的取值范围为　 　．

12．如图，在△ABC中，AB＝AC，BD平分∠ABC，交AC于点D，若BD＝BC，则∠A＝　 　度．

13．如图，在△ABC中，∠C＝45°，∠B＝60°，BC为+1，点P为边AB上一动点，过点P作PD⊥BC于点D，PE⊥AC于点E，则DE的最小值为　 　．

14．如图，射线OP与x轴正半轴的夹角为30°，点A是OP上一点，过点A作x轴的垂线与x轴交于点E．△AOE绕着点O逆时针旋转90°后能与△BOC重合，△BOC沿着y轴翻折能与△DOC重合，若点D恰好在抛物线y＝x2（x＞0）上，则点A的坐标是　 　．

三．解答题（共10小题，满分78分）
15．化简，求值：÷（m﹣1﹣），其中m＝．
16．如图是某教室里日光灯的四个控制开关（分别记为A、B、C、D），每个开关分别控制一排日光灯（开关序号与日光灯的排数序号不一定一致）．某天上课时，王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关．
（1）求王老师按下第一个开关恰好能打开第一排日光灯的概率；
（2）王老师按下两个开关恰好能打开第一排与第三排日光灯的概率是多少？请列表格或画树状图加以分析．

17．如图，在平面直角坐标系xOy中，△ABC的三个顶点的坐标分别是A（2，3），B（1，0），C（1，2）．
（1）在图中作出△ABC关于y轴对称的△A1B1C1；
（2）如果要使以B、C、D为顶点的三角形与△ABC全等，写出所有符合条件的点D坐标．

18．为保持水土，美化环境，W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树，并要求土路两侧树的棵数相等间距也相等，且首、尾两端均栽上树，现在学校已备好一批树苗，若间隔30米栽一棵，则缺少22棵；若间隔35米栽一棵，则缺少14棵
（1）求学校备好的树苗棵数．
（2）某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后，觉得两树间距太大，既不美观，又影响防风固沙的效果，决定无偿支援W中学300棵树苗．请问，这些树苗加上学校自己备好的树苗，间隔5米栽一棵，是否够用？
19．在抗击新型冠状病毒疫情期间，某校学生主动发起为武汉加油捐款活动，为了了解学生捐款金额（单位：元），随机调查了该校的部分学生，根据调查结果，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：

（Ⅰ）本次接受调查的学生人数为　 　，图①中m的值为　 　；
（Ⅱ）求统计的这组学生捐款数据的平均数、众数和中位数；
（Ⅲ）根据统计的这组学生捐款数据的样本数据，若该校共有1800名学生，估计该校此次捐款总金额为多少元？
20．如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，过点D作⊙O的切线DE交AC于点E．
（1）求证：∠A＝∠ADE；
（2）若AB＝25，DE＝10，弧DC的长为a，求DE、EC和弧DC围成的部分的面积S．（用含字母a的式子表示）．

21．某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y（升）与时间x（分钟）之间的关系如折线图所示，根据图象解答下列问题：
（1）洗衣机的进水时间是　 　分钟，清洗时洗衣机中的水量是　 　升．
（2）进水时y与x之间的关系式是　 　．
（3）已知洗衣机的排水速度是每分钟18升，如果排水时间为2分钟，排水结束时洗衣机中剩下的水量是　 　升．

22．如图，在△ABC中，∠ABC＝60°，点D，E分别为AB，BC上一点，BD＝BE，连接DE，DC，AC＝CD．
（1）如图1，若AC＝3，DE＝2，求EC的长；
（2）如图2，连接AE交DC于点F，点M为EC上一点，连接AM交DC于点N，若AE＝AM，求证：2DE＝MC；
（3）在（2）的条件下，若∠ACB＝45°，直接写出线段AD，MC，AC的等量关系．
23．如图1，正方形ABCD和正方形AEFG，连接DG，BE．
（1）发现
当正方形AEFG绕点A旋转，如图2，①线段DG与BE之间的数量关系是　 　；
②直线DG与直线BE之间的位置关系是　 　．
（2）探究
如图3，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG＝2AE，
证明：直线DG⊥BE．
（3）应用
在（2）情况下，连结GE（点E在AB上方），若GE∥AB，且AB＝，AE＝1，则线段DG是多少？（直接写出结论）

24．已知在平面直角坐标系中，抛物线y＝x2+3x﹣a2+a+2（a＞1）的图象交x轴于点A和点B（点A在点B左侧），与y轴交于点C，顶点为E．
（1）如图1，求线段AB的长度（用含a的式子表示）及抛物线的对称轴；
（2）如图2，当抛物线的图象经过原点时，在平面内是否存在一点P，使得以A、B、E、P为顶点的四边形能否成为平行四边形？如果能，求出P点坐标；如果不能，请说明理由；
（3）如图3，当a＝3时，若M点为x轴上一动点，连结MC，将线段MC绕点M逆时针旋转90°得到线段MN，连结AC、CN、AN，则△ACN周长的最小值为多少？












参考答案
一．选择题（共8小题，满分24分，每小题3分）
1．解：|﹣3|＝3，
故选：C．
2．解：将580 0000 0000用科学记数法表示应为5.8×1010．
故选：A．
3．解：根据俯视图的特征，应选C．
故选：C．
4．解：x﹣1＞0，
x＞1，
在数轴上表示为，
故选：C．
5．解：∵DE∥BC，
∴∠DEC＝∠ACF＝140°，
∴∠AED＝180°﹣140°＝40°，
∵∠ADE＝105°，
∴∠A＝180°﹣105°﹣40°＝35°，
故选：C．
6．解：∵DE∥BC，
∴△AED∽△ABC
∴，
设屏幕上的小树高是x，则，
解得x＝18cm．
故选：C．

7．解：设AB＝x米，
在Rt△ABC中，∵∠ACB＝45°，
∴BC＝AB＝x米，
则BD＝BC+CD＝x+100（米），
在Rt△ABD中，∵∠ADB＝30°，
∴tan∠ADB＝＝，即＝，
解得：x＝50+50 ≈137，
即建筑物AB的高度约为137米
故选：B．
8．解：作CD⊥AB于D，如图，
设B（t，﹣），
∵AB∥x轴，
∴A点的纵坐标为﹣，
∴A（2t，﹣），
∵△ABC是等腰直角三角形，CD⊥AB，
∴AD＝BD，CD＝AB，CD∥y轴，
∴D点坐标为（t，﹣），
∴C点的横坐标为t，
∵点C在反比例函数y＝﹣的图象上，
∴C（t，﹣），
∵AB＝t﹣2t＝﹣t，CD＝﹣+，
∴﹣+＝×（﹣t），
解得t＝﹣或t＝（舍去），
∴A（﹣，）．
故选：B．

二．填空题（共6小题，满分18分，每小题3分）
9．解：∵2＝＜，
∴＞2，
故答案为：＞．
10．解：x3•x2＝x5，
故答案为：x5
11．解：∵直线y＝2x与线段AB有公共点，
∴2n≥4，
∴n≥2
故答案为：n≥2
12．解：设∠ABD＝x°，
∵BD平分∠ABC，
∴∠DBC＝x°，
∵AB＝AC，
∴∠C＝∠ABC＝2x°，
又∵BD＝BC，
∴∠BDC＝∠C＝2x°，
又∵∠BDC＝∠A+∠ABD，即2x°＝∠A+x°，
∴∠A＝x°，
在△ABC中，∠A+∠ABC+∠C＝180°，
∴x+2x+2x＝180，
解得x＝36，
∴∠A＝36°，
故答案为36．
13．解：连接CP，如图：
∵PD⊥BC于点D，PE⊥AC于点E，
∴∠PDC＝∠PEC＝90°，
∴∠PDC+∠PEC＝180°，
∴C、D、P、E四点共圆，圆心为O，且直径为CP，
∵BC＝+1，∠B＝60°是定值，
∴直径CP最小时，∠DCE所对的弦DE最小，
即CP⊥AB时，DE最小，
连接OD、OE，
∵∠B＝60°，CP⊥AB，BC＝+1，
∴∠BCP＝30°，
∴BP＝BC＝，CP＝BP＝，
∴OD＝OE＝CP＝，
又∵∠ACB＝45°，
∴∠DOE＝2∠ACB＝90°，
∴△ODE是等腰直角三角形，
∴DE＝OD＝；
即DE的最小值为；
故答案为：．

14．解：设AE＝t，
在Rt△AOE中，∵∠AOE＝30°，
∴OE＝AE＝t，
∴A（t，t），
∵△AOE绕着点O逆时针旋转90°后能与△BOC重合，
∴BC＝AE＝t，OC＝OE＝t，
∴B（﹣t，t），
∵△BOC沿着y轴翻折能与△DOC重合
∴D（t，t），
把D（t，t）代入y＝x2得t2＝t，解得t1＝0（舍去），t2＝，
∴点A的坐标为（3，）．
故答案为（3，）．
三．解答题（共10小题，满分78分）
15．解：÷（m﹣1﹣）
＝•
＝•
＝，
当m＝时，原式＝．
16．解：（1）由题意可知王老师按下第一个开关恰好能打开第一排日光灯是：随机事件，概率为；

（2）画树状图如下：

所有出现的等可能性结果共有12种，其中满足条件的结果有2种．
即P（两个开关恰好能打开第一排与第三排日光灯）＝．
17．解：（1）如图所示，△A1B1C1即为所求；

（2）当△BCD与△BCA关于BC对称时，点D坐标为（0，3），
当△BCA与△CBD关于BC的中点对称时，点D坐标为（ 0，﹣1），
△BCA与△CBD关于BC的中垂线对称时，点D坐标为当（2，﹣1）．
18．解：（1）设学校备好的树苗为x棵，
依题意，得：30（﹣1）＝35（﹣1），
解得：x＝36．
答：学校备好的树苗为36棵．
（2）由（1）可知，校外土路长840米．
若间隔5米栽树，则共需树苗2（+1）＝338（棵），
300+36＝336（棵），
∵336＜338，
∴如果间隔5米栽一棵树，这些树苗不够用．
19．解：（Ⅰ）8+12+15+10+5＝50（人），
m%＝1﹣16%﹣24%﹣20%﹣10%＝30%，
故答案为：50，30；
（Ⅱ）这组数据的平均数是：20×16%+25×24%+30×30%+35×20%+40×10%＝29.2，
众数是30，中位数是30；
（Ⅲ）1800×29.2＝52560（元），
答：该校此次捐款总金额为52560元．
20．（1）证明：连接DC，
∵BC是⊙O直径，
∴∠BDC＝90°，
∴∠ADC＝90°，
∵∠C＝90°，BC为直径，
∴AC切⊙O于C，
∵过点D作⊙O的切线DE交AC于点E，
∴DE＝CE，
∴∠EDC＝∠ECD，
∵∠ACB＝∠ADC＝90°，
∴∠A+∠ACD＝90°，∠ADE+∠EDC＝90°，
∴∠A＝∠ADE；

（2）解：连接CD、OD、OE，
∵DE＝10，DE＝CE，
∴CE＝10，
∵∠A＝∠ADE，
∴AE＝DE＝10，
∴AC＝20，
∵∠ACB＝90°，AB＝25，
∴由勾股定理得：BC＝＝＝15，
∴CO＝OD＝，
∵的长度是a，
∴扇形DOC的面积是×a×＝a，
∴DE、EC和弧DC围成的部分的面积S＝××10+×10﹣a＝75﹣a．
21．解：（1）由图象可得，
洗衣机的进水时间是4分钟，清洗时洗衣机中的水量是40升，
故答案为：4，40；
（2）设进水时y与x之间的关系式是y＝kx，
4k＝40，得k＝10，
即进水时y与x之间的关系式是y＝10x，
故答案为：y＝10x；
（3）排水结束时洗衣机中剩下的水量是：40﹣18×2＝40﹣36＝4（升），
故答案为：4．
22．解：（1）如图1，
过点C作CG⊥AB于G，
∴∠AGC＝∠AGB＝90°，
∵AC＝CD，
∴AG＝DG，
设DG＝a，
∵BD＝BE，∠ABC＝60°，
∴△BDE是等边三角形，
∴BD＝DE＝2，
∴BG＝BD+DG＝2+a，
在Rt△BGC中，∠BCG＝90°﹣∠ABC＝30°，
∴BC＝2BG，CG＝BG＝6+a，
在Rt△DGC中，CD＝AC＝3，
根据勾股定理得，CG2+DG2＝CD2，
∴（6+a）2+a2＝90，
∴a＝或a＝（舍），
∴BC＝EC+BE＝EC+BD，
∴EC+BD＝2（BD+DG），
∴EC＝BD+2DG＝2+2a＝2+2×＝9﹣；

（2）如图2，在MC上取一点P，使MP＝DE，连接AP，
∵△BDE是等边三角形，
∴∠BED＝60°，BE＝DE，
∴∠DEC＝120°，BE＝PM，
∵AE＝AM，
∴∠AEM＝∠AME，
∴∠AEB＝∠AMP，
∴△ABE≌△APM（SAS），
∴∠APM＝∠ABC＝60°，
∴∠APC＝120°＝∠DEC，
过点M作AC的平行线交AP的延长线于Q，
∴∠MPQ＝∠APC＝120°＝∠DEC，
∵AC＝CD，
∴∠ADC＝∠DAC，
∴∠CDE＝180°﹣∠BDE﹣∠ADC＝180°﹣60°﹣∠DAC＝120°﹣∠DAC，
在△ABC中，∠ACB＝180°﹣∠ABC﹣∠DAC＝120°﹣∠DAC＝∠CDE，
∵MQ∥AC，
∴∠PMQ＝∠ACB，
∴∠PMQ＝∠EDC，
∴△MPQ≌△DEC（ASA），
∴MQ＝CD，
∵AC＝MQ，
∴△APC≌△QPM（AAS），
∴CP＝MP，
∴CM＝MP+CP＝2DE；

（3）如备用图，在MC上取一点P，使PM＝DE，
由（2）知，MC＝2CP＝2DE，
由（2）知，△ABE≌△APM，
∴AB＝AP，
∵∠ABC＝60°，
∴△ABP是等边三角形，
∴BP＝AB，
∵BE＝BD，
∴PE＝AD，
∴BC＝BE+PE+CP＝DE+PE+DE＝2DE+AD＝MC+AD，
过点A作AH⊥BC于H，设BH＝m，
在Rt△ABH中，AH＝BH＝m，
在Rt△ACH中，∠ACB＝45°，
∴∠CAH＝90°﹣∠ACB＝45°＝∠ACB，
∴CH＝AH＝m，AC＝AH＝m，
∵MC+AD＝BC＝BH+CH＝m+m＝（1+）m，
∴MC+AD＝AC．



23．解：（1）①∵四边形ABCD和四边形AEFG是正方形，
∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，
∴∠BAE＝∠DAG，
在△ABE和△DAG中，，
∴△ABE≌△DAG（SAS），
∴BE＝DG；
②如图2，延长BE交AD于G，交DG于H，
由①知，△ABE≌△DAG，
∴∠ABE＝∠ADG，
∵∠AQB+∠ABE＝90°，
∴∠AQB+∠ADG＝90°，
∵∠AQB＝∠DQH，
∴∠DQH+∠ADG＝90°，
∴∠DHB＝90°，
∴BE⊥DG，
故答案为：BE＝DG，BE⊥DG；
（2）∵四边形ABCD与四边形AEFG都为矩形，
∴∠BAD＝∠DAG，
∴∠BAE＝∠DAG，
∵AD＝2AB，AG＝2AE，
∴＝，
∴△ABE∽△ADG，
∴∠ABE＝∠ADG，
∵∠AGB+∠ABE＝90°，
∴∠AGB+∠ADG＝90°，
∵∠AGB＝∠DGH，
∴∠DGH+∠ADG＝90°，
∴∠DHB＝90°，
∴BE⊥DG；
（3）如图3，（为了说明点B，E，F在同一条线上，特意画的图形）
EG与AD的交点记作M，
∵EG∥AB，
∴∠DME＝∠DAB＝90°，
在Rt△AEG中，AE＝1，
∴AG＝2AE＝2，
根据勾股定理得，EG＝，
∵AB＝，
∴EG＝AB，
∵EG∥AB，
∴四边形ABEG是平行四边形，
∴AG∥BE，
∵AG∥EF，
∴点B，E，F在同一条直线上如图4，
∴∠AEB＝90°，
在Rt△ABE中，根据勾股定理得，BE＝＝2，
由（2）知，△ABE∽△ADG，
∴＝，
∴，
∴DG＝4．
图3


24．解：（1）当y＝0时，x2+3x﹣a2+a+2＝0，
∴[x﹣（a﹣2）][x+（a+1）]＝0，
∴x＝a﹣2，或x＝﹣a﹣1，
∵点A在点B左侧，
∴A（﹣a﹣1，0），B（a﹣2，0），
∴AB＝a﹣2﹣（﹣a﹣1）＝2a﹣1，
抛物线的对称轴为x＝＝﹣，即抛物线的对称轴为x＝﹣；
（2）存在，理由如下：
∵抛物线y＝x2+3x﹣a2+a+2（a＞1）的图象经过原点，a＞1，
∴﹣a2+a+2＝0，
解得：a＝2，或a＝﹣1（舍去），
∴a＝2，
∴A（﹣3，0），B（0，0），y＝x2+3x＝（x+）2﹣，
∴E（﹣，﹣），
分情况讨论，如图2所示：
①若AB为平行四边形的边，则P点坐标为（，﹣）或（﹣，﹣）；
②若AB为平行四边形的对角线，则P点坐标为（﹣，）；
综上所述，在平面内存在一点P，使得以A、B、E、P为顶点的四边形成为平行四边形，P点坐标为（，﹣）或（﹣，﹣）或（﹣，）；
（3）当a＝3时，y＝x2+3x﹣4，
此时A（﹣4，0），B（1，0），C（0，﹣4），
∴OA＝4，OC＝4，
设M（t，0），
∵将线段MC绕点M逆时针旋转90°得到线段MN，
∴OM＝﹣t，
过点M作EF⊥x轴，过点N作NE⊥EF于点E，过点C作CF⊥EF于点F，如图3所示：
则∠MEN＝∠CFM＝90°，
由旋转的性质得：MN＝MC，∠CMN＝90°，
∴∠EMN+∠CMF＝∠CMF+∠FCM＝90°，
∴∠EMN＝∠FCM，
在△MNE和△CMF中，，
∴△MNE≌△CMF（AAS），
∴ME＝CF＝OM＝﹣t，EN＝MF＝OC＝4，
∴点N的横坐标为Nx＝4+t，点N的纵坐标为Ny＝﹣t，
∴y＝﹣x+4，
∴点N在直线l：y＝﹣x+4上运动，
设直线l交x轴于点G，则G（4，0），
若使△ACN的周长最小，即使AN+CN最小，
∴作点A关于l的对称点A'，连接A'C，A'N，
则AN＝A'N，
当A'、N、C三点共线时，AN+CN最小＝A'C，
由题意得：∠A'AO＝45°，∠CAO＝45°，
∴∠CAA'＝90°，
∵G（4，0），
∴AG＝OA+OG＝8，AA'＝8，
∵AC＝＝4，
∴A'C＝＝4，
∴A'C+AC＝4+4，
∵△ACN的周长＝AN+CN+AC，
∴△ACN周长的最小值为A'C+AC＝4+4．