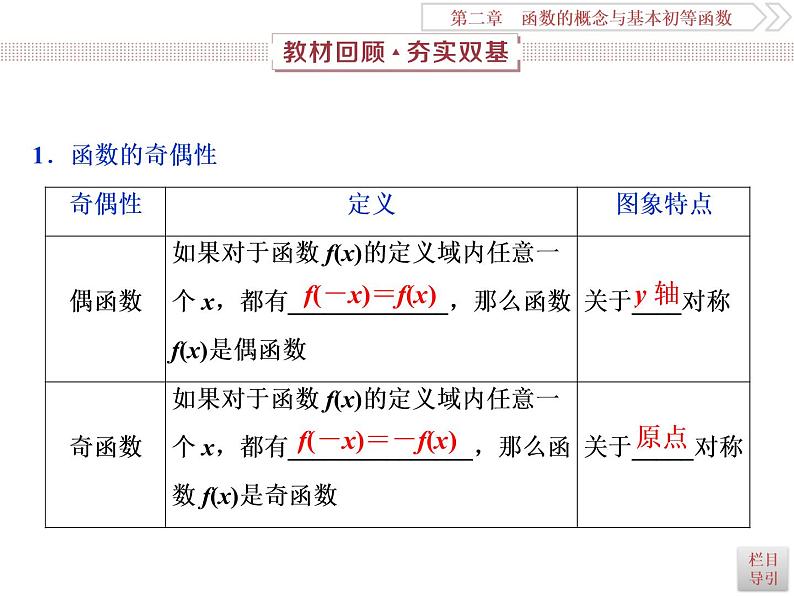
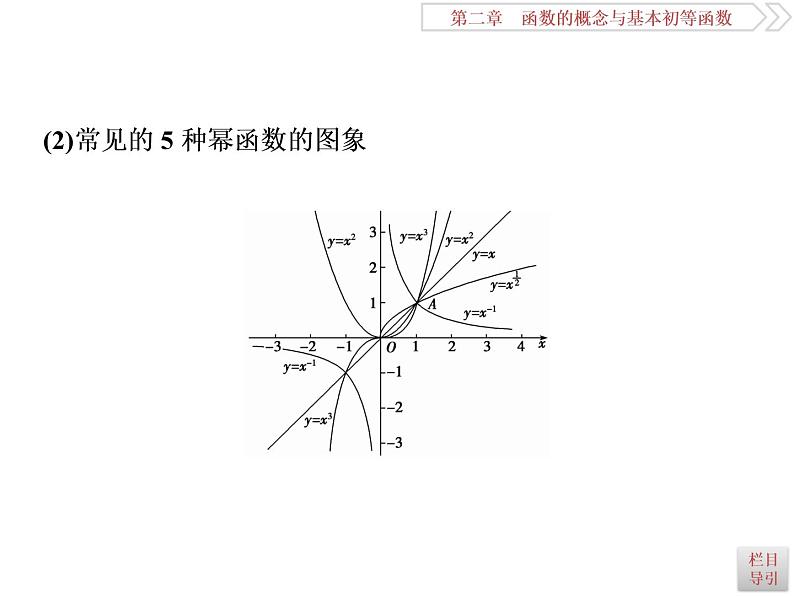
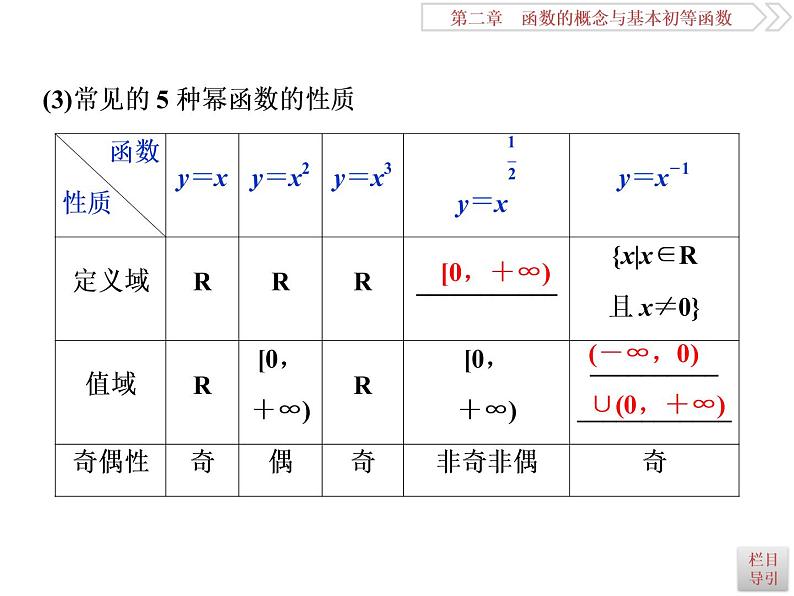
2021届高考数学（理科）人教版 1轮复习资料（课件+达标练习） 第二章　函数的概念与基本初等函数 (共21份打包)

一、选择题1．函数f(x)＝1－e|x|的图象大致是(　　)解析：选A.将函数解析式与图象对比分析，因为函数f(x)＝1－e|x|是偶函数，且值域是(－∞，0]，只有A满足上述两个性质．2．化简4a·b－÷的结果为(　　)A．－ B．－C．－ D．－6ab解析：选C.原式＝a－b－－＝－6ab－1＝－，故选C.3．已知实数a，b满足等式＝，下列五个关系式：①0＜b＜a；②a＜b＜0；③0＜a＜b；④b＜a＜0；⑤a＝b.其中不可能成立的关系式有(　　)A．1个 B．2个C．3个 D．4个解析：选B.函数y1＝与y2＝的图象如图所示．由＝得，a＜b＜0或0＜b＜a或a＝b＝0.故①②⑤可能成立，③④不可能成立．4．若函数f(x)＝a|2x－4|(a>0，a≠1)，满足f(1)＝，则f(x)的单调递减区间是(　　)A．(－∞，2] B．[2，＋∞)C．[－2，＋∞) D．(－∞，－2]解析：选B.由f(1)＝得a2＝，所以a＝或a＝－(舍去)，即f(x)＝.由于y＝|2x－4|在(－∞，2]上递减，在[2，＋∞)上递增，所以f(x)在(－∞，2]上递增，在[2，＋∞)上递减，故选B.5．设a＝1.90.9，b＝0.91.9，c＝0.99.1，则a，b，c的大小关系为(　　)A．a＞b＞c B．b＞a＞cC．a＞c＞b D．c＞a＞b解析：选A.因为函数y＝0.9x在R上是减函数，所以0.91.9＞0.99.1，且0.91.9＜0.90＝1.即c＜b＜1.又函数y＝1.9x在R上是增函数．所以1.90.9＞1.90＝1即a＞1.所以a＞b＞c.故选A.6．若函数f(x)＝是奇函数，则使f(x)>3成立的x的取值范围为(　　)A．(－∞，－1) B．(－1，0)C．(0，1) D．(1，＋∞)解析：选C.因为f(x)为奇函数，所以f(－x)＝－f(x)，即＝－，整理得(a－1)(2x＋1)＝0，所以a＝1，所以f(x)>3即为>3，当x>0时，2x－1>0，所以2x＋1>3·2x－3，解得0<x<1；当x<0时，2x－1<0，所以2x＋1<3·2x－3，无解．所以x的取值范围为(0，1)．二、填空题7．函数y＝的值域是________．解析：因为4x>0，所以16－4x<16，所以0≤16－4x<16，即0≤y<4.答案：[0，4)8．若函数f(x)＝ax－1(a＞0，a≠1)的定义域和值域都是[0，2]，则实数a＝________．解析：当a>1时，f(x)＝ax－1在[0，2]上为增函数，则a2－1＝2，所以a＝±，又因为a>1，所以a＝.当0<a<1时，f(x)＝ax－1在[0，2]上为减函数，又因为f(0)＝0≠2，所以0<a<1不成立．综上可知，a＝.答案：9．若函数f(x)＝2|x－a|(a∈R)满足f(1＋x)＝f(1－x)，且f(x)在[m，＋∞)上单调递增，则实数m的最小值等于________．解析：因为f(x)＝2|x－a|，所以f(x)的图象关于x＝a对称．又由f(1＋x)＝f(1－x)，知f(x)的图象关于直线x＝1对称，故a＝1，且f(x)的增区间是[1，＋∞)，由函数f(x)在[m，＋∞)上单调递增，知[m，＋∞)⊆[1，＋∞)，所以m≥1，故m的最小值为1.答案：110.已知函数y＝ax＋b(a>0，且a≠1，b>0)的图象经过点P(1，3)，如图所示，则＋的最小值为________，此时a，b的值分别为________．解析：由函数y＝ax＋b(a>0且a≠1，b>0)的图象经过点P(1，3)，得a＋b＝3，所以＋＝1，又a>1，则＋＝(＋)＝2＋＋＋≥＋2　＝，当且仅当＝，即a＝，b＝时取等号，所以＋的最小值为.答案：　，三、解答题11．已知函数f(x)＝b·ax(其中a，b为常量，且a>0，a≠1)的图象经过点A(1，6)，B(3，24)．若不等式＋－m≥0在x∈(－∞，1]上恒成立，求实数m的取值范围．解：把A(1，6)，B(3，24)代入f(x)＝b·ax，得结合a>0，且a≠1，解得所以f(x)＝3·2x.要使＋≥m在x∈(－∞，1]上恒成立，只需保证函数y＝＋在(－∞，1]上的最小值不小于m即可．因为函数y＝＋在(－∞，1]上为减函数，所以当x＝1时，y＝＋有最小值.所以只需m≤即可．即m的取值范围为.12．已知函数f(x)＝.(1)若a＝－1，求f(x)的单调区间；(2)若f(x)有最大值3，求a的值．解：(1)当a＝－1时，f(x)＝，令g(x)＝－x2－4x＋3，由于g(x)在(－∞，－2)上单调递增，在(－2，＋∞)上单调递减，而y＝在R上单调递减，所以f(x)在(－∞，－2)上单调递减，在(－2，＋∞)上单调递增，即函数f(x)的单调递增区间是(－2，＋∞)，单调递减区间是(－∞，－2)．(2)令g(x)＝ax2－4x＋3，f(x)＝，由于f(x)有最大值3，所以g(x)应有最小值－1，因此必有解得a＝1，即当f(x)有最大值3时，a的值为1.