




















































- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十章 计数原理、概率、随机变量及其分布列 (共17份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十三章 选考部分 (共11份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第九章 平面解析几何 (共24份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习) 第十一章 统计与统计案例 (共7份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习) 第七章 不等式 (共7份打包) 课件 1 次下载
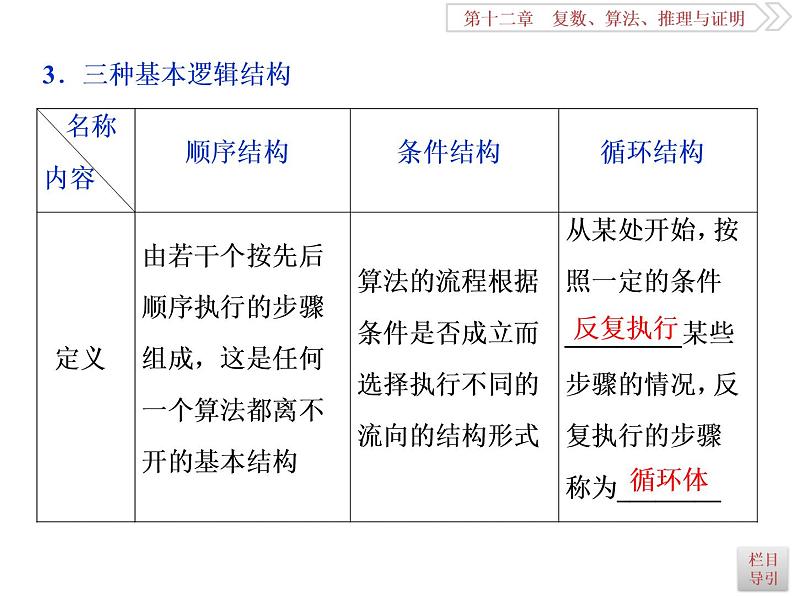
2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十二章 复数、算法、推理与证明 (共11份打包)
展开]
一、选择题
1.用数学归纳法证明等式“1+2+22+…+2n+2=2n+3-1”,验证n=1时,等号左边的式子应为( )
A.1 B.1+2
C.1+2+22 D.1+2+22+23
答案:D
2.若f(n)=1+++…+(n∈N*),则f(1)等于( )
A.1 B.
C.1++++ D.1+
答案:C
3.已知n为正偶数,用数学归纳法证明1-+-+…-=2时,若已假设n=k(k≥2,且k为偶数)时命题为真,则还需要用归纳假设再证( )
A.n=k+1时等式成立
B.n=k+2时等式成立
C.n=2k+2时等式成立
D.n=2(k+2)时等式成立
答案:B
4.在用数学归纳法证明“平面内有n条(n≥2)直线,任何两条不平行,任何三条不过同一个点的交点个数为”时,第一步验证n0等于( )
A.1 B.2
C.3 D.4
答案:B
二、填空题
5.用数学归纳法证明1+2+3+…+n2=,当n=k+1时,左端应在n=k的基础上增添的代数式是 .
答案:(k2+1)+(k2+2)+…+(k+1)2
6.当n∈N*时,1·2+2·3+…+n(n+1)=n(n+1)(an+b)恒成立,则a-b= W.
解析:由n=1,2得.
解得a=,b=.所以a-b=-.
答案:-
三、解答题
7.用数学归纳法证明:+++…+=(n∈N*).
证明:(1)当n=1时,左边==,
右边==,
左边=右边,即等式成立.
(2)假设n=k(k∈N*)时等式成立,即+++…+=,
则当n=k+1时,+++…++
=+====.
所以当n=k+1时,等式也成立,
由(1)(2)可知,对于一切n∈N*等式都成立.
8.设数列{an}的前n项和为Sn,满足Sn=2nan+1-3n2-4n,n∈N*,且S3=15.
(1)求a1,a2,a3的值;
(2)猜想数列{an}的通项公式,并用数学归纳法证明.
解:(1)由Sn=2nan+1-3n2-4n,得S2=4a3-20,S3=S2+a3=5a3-20.又S3=15,所以a3=7,S2=4a3-20=8.
又S2=S1+a2=(2a2-7)+a2=3a2-7,
所以a2=5,a1=S1=2a2-7=3.
综上知a1=3,a2=5,a3=7.
(2)由(1)猜想an=2n+1(n∈N*),以下用数学归纳法证明:
①当n=1时,结论显然成立;
②假设当n=k(k∈N*,且k≥2)时,有ak=2k+1成立,
则Sk=3+5+7+…+(2k+1)
=×k=k(k+2).
又Sk=2kak+1-3k2-4k,
所以k(k+2)=2kak+1-3k2-4k,
解得ak+1=2k+3=2(k+1)+1,
即当n=k+1时,结论成立.
由①②知,数列{an}的通项公式为an=2n+1(n∈N*).
9.已知点Pn(an,bn)满足an+1=an·bn+1,bn+1=(n∈N*)且点P1的坐标为(1,-1).
(1)求过点P1,P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N*,点Pn都在(1)中的直线l上.
解:(1)由P1的坐标为(1,-1)知a1=1,b1=-1.
所以b2==,a2=a1·b2=.
所以点P2的坐标为.
所以直线l的方程为2x+y=1.
(2)证明:①当n=1时,
2a1+b1=2×1+(-1)=1成立.
②假设n=k(k∈N*,k≥1)时,2ak+bk=1成立,
则2ak+1+bk+1=2ak·bk+1+bk+1
=(2ak+1)===1,
所以当n=k+1时,命题也成立.
由①②知,对n∈N*,都有2an+bn=1,
即点Pn都在直线l上.
10.是否存在a,b∈R,使得等式13+23+33+…+n3=对于一切n∈N*均成立.并说明理由.
解:当n=1,2时,
解之得a=b=1.
所以存在a=b=1使得等式13+23+33+…+n3==对于n=1,2成立.
下面用数学归纳法探讨13+23+33+…+n3=(n∈N)*是否正确.
(1)当n=1时,左边=13=1,右边==1.等式成立.
(2)假设n=k(k∈N*)时,等式成立.
即13+23+33+…+k3=,则当n=k+1时,13+23+33+…+k3+(k+1)3=+(k+1)3==
=,
即n=k+1时,等式也成立.
由(1)(2)可知,存在a=b=1,使得等式13+23+33+…+n3=对于一切n∈N*均成立.








