


















































- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第四章 三角函数与解三角形 (共15份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十章 计数原理、概率、随机变量及其分布列 (共17份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十二章 复数、算法、推理与证明 (共11份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第九章 平面解析几何 (共24份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习) 第十一章 统计与统计案例 (共7份打包) 课件 1 次下载
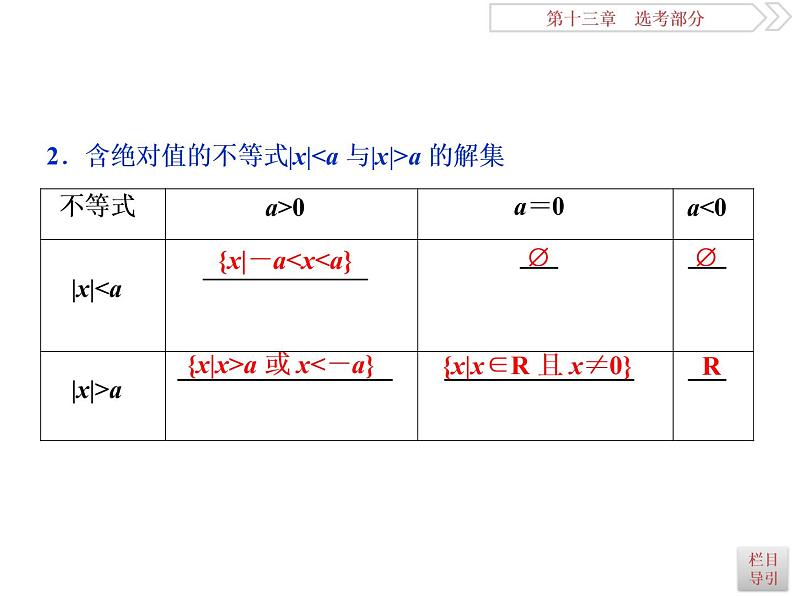
2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十三章 选考部分 (共11份打包)
展开1.设x,y,z∈R,2x-y-2z=6,试求x2+y2+z2的最小值.
解:考虑以下两组向量u=(2,-1,-2),v=(x,y,z),
根据柯西不等式(u·v)2≤|u|2·|v|2,
得[2x+(-1)y+(-2)z]2≤[22+(-1)2+(-2)2](x2+y2+z2),
即(2x-y-2z)2≤9(x2+y2+z2),
将2x-y-2z=6代入其中,
得36≤9(x2+y2+z2),
即x2+y2+z2≥4,
故x2+y2+z2的最小值为4.
2.设x,y,z∈R,x2+y2+z2=25,试求x-2y+2z的最大值与最小值.
解:根据柯西不等式,有(1·x-2·y+2·z)2≤[12+(-2)2+22](x2+y2+z2),
即(x-2y+2z)2≤9×25,所以-15≤x-2y+2z≤15,
故x-2y+2z的最大值为15,最小值为-15.
3.已知大于1的正数x,y,z满足x+y+z=3.求证:++≥.
证明:由柯西不等式及题意得,
·[(x+2y+3z)+(y+2z+3x)+(z+2x+3y)]≥(x+y+z)2=27.
又(x+2y+3z)+(y+2z+3x)+(z+2x+3y)=6(x+y+z)=18,
所以++≥=,
当且仅当x=y=z=时,等号成立.
4.已知关于x的不等式|x+a|<b的解集为{x|2<x<4}.
(1)求实数a,b的值;
(2)求+的最大值.
解:(1)由|x+a|<b,可得-b-a<x<b-a,
所以-b-a=2且b-a=4.
解得a=-3,b=1.
(2)利用柯西不等式,可得+=(+)≤=×=2,当且仅当=,即t=2时等号成立.
当t=2时,+的最大值为2.
5.设函数f(x)=|x-4|+|x-3|,f(x)的最小值为m.
(1)求m的值;
(2)当a+2b+3c=m(a,b,c∈R)时,求a2+b2+c2的最小值.
解:(1)法一:f(x)=|x-4|+|x-3|≥|(x-4)-(x-3)=1,故函数f(x)的最小值为1,即m=1.
法二:f(x)=
当x≥4时,f(x)≥1;当x<3时,f(x)>1;当3≤x<4时,f(x)=1,故函数f(x)的最小值为1,即m=1.
(2)(a2+b2+c2)(12+22+32)≥(a+2b+3c)2=1,故a2+b2+c2≥,当且仅当a=,b=,c=时取等号.
故a2+b2+c2的最小值为.
6.已知a,b,c∈R+,且a+b+c=3.
求证:++≥3.
证明:因为a,b,c∈R+,由柯西不等式得
≥
即(a+b+c)≥(b+c+a)2
所以++≥a+b+c=3.即++≥3.
1.已知函数f(x)=|x-1|+|x-5|,g(x)=.
(1)求f(x)的最小值;
(2)记f(x)的最小值为m,已知实数a,b满足a2+b2=6,求证:g(a)+g(b)≤m.
解:(1)因为f(x)=|x-1|+|x-5|,
所以f(x)=|x-1|+|x-5|=,
所以f(x)min=4.
(2)证明:由(1)知m=4.由柯西不等式得
[1×g(a)+1×g(b)]2≤(12+12)[g2(a)+g2(b)],
即[g(a)+g(b)]2≤2(a2+b2+2),
又g(x)=>0,a2+b2=6,
所以g(a)+g(b)≤4(当且仅当a=b=时取等号).
即g(a)+g(b)≤m.
2.已知a>0,b>0,c>0,函数f(x)=|x+a|+|x-b|+c的最小值为4.
(1)求a+b+c的值;
(2)求a2+b2+c2的最小值.
解:(1)因为f(x)=|x+a|+|x-b|+c≥|(x+a)-(x-b)|+c=|a+b|+c,
当且仅当-a≤x≤b时,等号成立.
又a>0,b>0,所以|a+b|=a+b,
所以f(x)的最小值为a+b+c,
又f(x)的最小值为4,所以a+b+c=4.
(2)由(1)知a+b+c=4,由柯西不等式得×(4+9+1)≥
=(a+b+c)2=16,
故a2+b2+c2≥.
当且仅当==,即a=,b=,c=时等号成立.故a2+b2+c2的最小值为.








