








































































- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习) 第三章 导数及其应用 (共9份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第五章 平面向量 (共7份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十章 计数原理、概率、随机变量及其分布列 (共17份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十三章 选考部分 (共11份打包) 课件 1 次下载
- 2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第十二章 复数、算法、推理与证明 (共11份打包) 课件 1 次下载
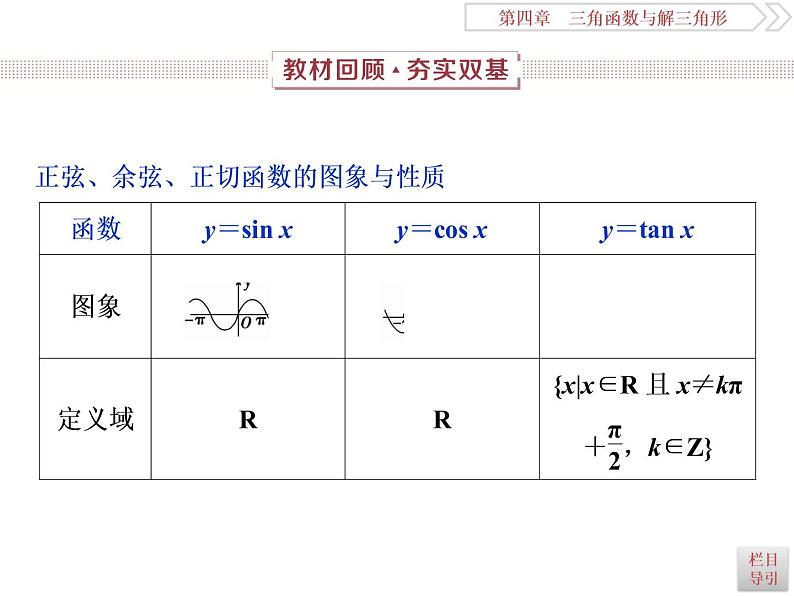
2021届高考数学(理科)人教版 1轮复习资料(课件+达标练习)第四章 三角函数与解三角形 (共15份打包)
展开一、选择题
1.要得到函数f(x)=cos 2x的图象,只需将函数g(x)=sin 2x的图象( )
A.向左平移个周期 B.向右平移个周期
C.向左平移个周期 D.向右平移个周期
解析:选C.因为f(x)=cos 2x=sin=sin,且函数g(x)的周期为=π,所以将函数g(x)=sin 2x的图象向左平移个单位长度,即向左平移个周期,可得函数f(x)=cos 2x的图象,故选C.
2.将函数y=cos的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位长度,所得函数图象的一条对称轴为( )
A.x= B.x=
C.x= D.x=π
解析:选A.将函数y=cos图象上各点的横坐标伸长到原来的2倍(纵坐标不变)时,得到函数y=cos的图象;再将此函数的图象向左平移个单位长度后,得到函数y=cos=cos的图象.该函数图象的对称轴为-=kπ(k∈Z),即x=2kπ+(k∈Z).结合选项,只有A符合,故选A.
3.函数f(x)=sin(ωx+φ)的部分图象如图所示,则f(x)的单调递增区间为( )
A.(-1+4kπ,1+4kπ),k∈Z
B.(-3+8kπ,1+8kπ),k∈Z
C.(-1+4k,1+4k),k∈Z
D.(-3+8k,1+8k),k∈Z
解析:选D.由题图,知T=4×(3-1)=8,所以ω==,所以f(x)=sin.把(1,1)代入,得sin=1,即+φ=+2kπ(k∈Z),又|φ|<,所以φ=,所以f(x)=sin.由2kπ-≤x+≤2kπ+(k∈Z),得8k-3≤x≤8k+1(k∈Z),所以函数f(x)的单调递增区间为(8k-3,8k+1)(k∈Z),故选D.
4.已知函数f(x)=sin(ωx+φ)的部分图象如图所示,则=( )
A.-1 B.
C. D.1
解析:选B.由已知易得ω=2,由五点法作图可知2×+φ=,得φ=,即f(x)=sin.故f=1,f=,f=-,f=-1,f=-,f=,故=336×(1+--1-+)+f+f=.故选B.
5.将函数f(x)=sin(2x+φ)的图象向左平移个单位长度后关于原点对称,则函数f(x)在上的最小值为( )
A.- B.-
C. D.
解析:选A.将f(x)=sin(2x+φ)的图象向左平移个单位长度得y=sin=sin的图象,该图象关于原点对称,即为奇函数,则+φ=kπ(k∈Z),且|φ|<,所以φ=-,即f(x)=sin(2x-),当x∈时,2x-∈,所以当2x-=-,即x=0时,f(x)取得最小值,最小值为-,选A.
6.将函数f(x)=sin 2x的图象向右平移φ个单位后得到函数g(x)的图象.若对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=,则φ=( )
A. B.
C. D.
解析:选D.由已知得g(x)=sin(2x-2φ),满足|f(x1)-g(x2)|=2,不妨设此时y=f(x)和y=g(x)分别取得最大值与最小值,又|x1-x2|min=,令2x1=,2x2-2φ=-,此时|x1-x2|==,又0<φ<,故φ=,选D.
二、填空题
7.已知函数f(x)=Atan(ωx+φ),y=f(x)的部分图象如图,则f=________.
解析:由题图可知,T=2=,
所以ω=2,所以2×+φ=kπ+(k∈Z).
又|φ|<,所以φ=.
又f(0)=1,所以Atan=1,得A=1,
所以f(x)=tan,
所以f=tan=tan=.
答案:
8.函数f(x)=sin ωx(ω>0)的图象向左平移个单位长度,所得图象经过点,则ω的最小值是________.
解析:依题意得,函数f=sin(ω>0)的图象过点,于是有f=sin[ω(+)]=sin ωπ=0(ω>0),ωπ=kπ,k∈Z,即ω=k∈Z,因此正数ω的最小值是1.
答案:1
9.已知函数f(x)=sin(ωx+φ)的图象上的一个最高点和与它相邻的一个最低点的距离为2,且过点,则函数f(x)=________.
解析:依题意得 =2,则=2,即ω=,所以f(x)=sin,由于该函数图象过点,因此sin(π+φ)=-,即sin φ=,而-≤φ≤,故φ=,所以f(x)=sin.
答案:sin
10.将函数f(x)=sin(ωx+φ)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sin x的图象,则f=________.
解析:y=sin xy=sin
y=sin,
即f(x)=sin,
所以f=sin=sin=.
答案:
三、解答题
11.某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入了部分数据,如下表:
ωx+φ | 0 | π | 2π | ||
x |
|
|
| ||
Asin(ωx+φ) | 0 | 5 |
| -5 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为,求θ的最小值.
解:(1)根据表中已知数据,解得A=5,ω=2,φ=-,数据补全如下表:
ωx+φ | 0 | π | 2π | ||
x | π | ||||
Asin(ωx+φ) | 0 | 5 | 0 | -5 | 0 |
且函数解析式为f(x)=5sin.
(2)由(1)知 f(x)=5sin,
则g(x)=5sin.
因为函数y=sin x图象的对称中心为(kπ,0),k∈Z,
令2x+2θ-=kπ,
解得x=+-θ,k∈Z.
由于函数y=g(x)的图象关于点成中心对称,
所以令+-θ=,
解得θ=-,k∈Z.
由θ>0可知,当k=1时,θ取得最小值.
12.已知f(x)=2sin+a+1.
(1)若x∈R,求f(x)的单调递增区间;
(2)当x∈时,f(x)的最大值为4,求a的值;
(3)在(2)的条件下,求满足f(x)=1且x∈[-π,π]的x集合.
解:(1)由2kπ-≤2x+≤2kπ+,k∈Z,
可得x∈(k∈Z),
所以f(x)的单调递增区间为(k∈Z).
(2)当x=时,f(x)取最大值,
f=2sin+a+1=a+3=4,
所以a=1.
(3)由f(x)=2sin+2=1可得
sin=-,
则2x+=+2kπ或2x+=π+2kπ,k∈Z,
即x=+kπ或x=+kπ,k∈Z,
又x∈[-π,π],
可解得x=-,-,,,
所以x的集合为.
1.设函数f(x)=sin+sin,其中0<ω<3.已知f=0.
(1)求ω;
(2)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在上的最小值.
解:(1)因为f(x)=sin+sin,
所以f(x)=sin ωx-cos ωx-cos ωx
=sin ωx-cos ωx
=
=sin.
由题设知f=0,
所以-=kπ,k∈Z.
故ω=6k+2,k∈Z,又0<ω<3,
所以ω=2.
(2)由(1)得f(x)=sin,
所以g(x)=sin=sin.
因为x∈,
所以x-∈,
当x-=-,
即x=-时,g(x)取得最小值-.
2.某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道(单位:米)曲线段是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]的图象且最高点为B(-1,4),在y轴右侧的观光道曲线段是以CO为直径的半圆弧.
(1)试确定A,ω和φ的值;
(2)现要在y轴右侧的半圆中修建一条步行道CDO,点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米).点D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设∠DCO=θ(弧度),试用θ来表示修建步行道CDO的造价预算,并求该造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
解:(1)因为最高点为B(-1,4),所以A=4.
由图可得=-1-(-4)=3,
所以T=12,
因为T==12,
所以ω=,
所以4=4sin,即sin=1,又0<φ<π,所以φ=.
(2)由(1)知y=4sin(x+),x∈[-4,0],得点C(0,2),
即CO=2,取CO的中点F,连接DF,DO,
因为弧为半圆弧,
所以∠DFO=2θ,∠CDO=90°,
即=2θ×=2θ,
则圆弧段的造价预算为2θ万元,
在Rt△CDO中,CD=2cos θ,
则直线段CD的造价预算为4cos θ万元,
所以步行道CDO的造价预算g(θ)=4cos θ+2θ,θ∈.
由g′(θ)=4(-sin θ)+2=2(1-2sin θ),得当θ=时,g′(θ)=0,
当θ∈时,g′(θ)>0,
即g(θ)在上单调递增;
当θ∈时,g′(θ)<0,
即g(θ)在上单调递减.
所以g(θ)在θ=时取得极大值也是最大值为6+π,即修建步行道CDO的造价预算的最大值为万元.








